动态规划算法 **动态规划(dynamic programming)**是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。这个方法很类似于数学上的数学归纳法。
定义 动态规划实际上是一类题目的总称，并不是指某个固定的算法。动态规划的意义就是通过采用递推（或者分而治之） 的策略，通过解决大问题的子问题从而解决整体的做法。
动态规划的核心思想 是巧妙的将问题拆分成多个子问题，通过计算子问题而得到整体问题的解。而子问题又可以拆分成更多的子问题，从而用类似递推迭代的方法解决要求的问题。
动态规划的本质，是对问题状态的定义 和状态转移方程的定义
拆分问题 ，靠的就是状态的定义 和状态转移方程的定义 。
参考资料：动态规划
动态规划实质
动态规划算法通常基于一个递推公式及一个或多个初始状态。当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度，因此它比回溯法、暴力法等要快许多。
每个阶段只有一个状态->递推；
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到
这个性质叫做最优子结构；
而不管之前这个状态是如何得到的
这个性质叫做无后效性。
动态规划和分治的区别 动态规划也是一种分治思想（比如其状态转移方程就是一种分治），但与分治算法不同的是，分治算法是把原问题分解为若干个子问题，自顶向下求解子问题，合并子问题的解，从而得到原问题的解 。动态规划也是把原始问题分解为若干个子问题，然后自底向上，先求解最小的子问题，把结果存在表格中，在求解大的子问题时，直接从表格中查询小的子问题的解 ，避免重复计算，从而提高算法效率。（因为分治策略会反复求解公共子问题）
可以采用动态规划求解的问题的一般要具有3个性质 1、最优化子结构原理 如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。最有子结构是使用动态规划的最基本的条件，如果不具有最优子结构性质，就不可以使用动态规划解决。证明的例子
如何证明问题的最优解满足最优子结构性呢？
即证明：作为构成原问题最优解的组成部分，对应每个子问题的部分应是该子问题的最优解。
“剪切-粘贴”（cut-and-paste）技术：
本质上是反证法证明：假定原问题最优解中对应于某个子问题的部分解不是该子问题的最优解，而存在“更优的子解”，那么我们可以从原问题的解中“剪切”掉这一部分，而将“更优的子解”粘贴进去，从而得到一个比最优解“更优”的解，这与最初的解是原问题的最优解的前提假设相矛盾。因此，不可能存在“更优的子解”。——所以，原问题的子问题的解必须是其最优解，最优子结构性成立。
2、子问题重叠 子问题重叠不是使用动态规划的必要条件，但是问题存在子问题重叠的特性更能够充分彰显动态规划的优势。
举个例子：求斐波那契数列时fib(8)=fib(7)+fib(6)，其中fib(8)的最优解就包含了子问题fib(7)的最优解和子问题fib(6)的最优解，反过来讲只要我们求解出子问题的最优解，那么就可以构造出问题的最优解，这也就是为什么最优子结构是求解动态规划的必要条件。fib(7)和fib(6)中有相同的子问题fib(5)，这就是子问题重叠。
3、无后效性 即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。
动态规划的维数 斐波那契数列问题中的递归方程中只涉及一个变量i，所以是一维的动态规划，最长公共子序列问题中，递归方程中涉及两个变量，是二维的动态规划。一个很直观的理解就是，动态规划在从子问题的最优解来得到问题的最优解的过程中所填写的那张表格是几维的，就是几维的动态规划。
最长公共子串（Longest Common Substring）与最长公共子序列（Longest Common Subsequence）的区别： 子串要求在原字符串中是连续的，而子序列则只需保持相对顺序一致，并不要求连续。
如何验证最优子结构特性 先写出问题的最优解和子问题的最优解的关系，然后假定问题的最优解成立（上面关系的左边成立），看能否得到子问题的最优解就是关系式右边的子问题最优解的形式，如果是就验证了最优子结构（一般用反证法）。
解题核心 动态规划的解题核心主要分为两步：
第一步：状态的定义 第二步：状态转移方程的定义
在这里，我们为了避免混淆用“状态”这个词来替代“问题”这个词。“问题”表示的含义类似：题目、要求解的内容、题干中的疑问句这样的概念。状态表示我们在求解问题之中对问题的分析转化。
第一步：状态的定义 —————-刻画了一个最优解的结构特征（最优子结构性）
有的问题过于抽象，或者过于啰嗦干扰我们解题的思路，我们要做的就是将题干中的问题进行转化（换一种说法，含义不变）。转化成一系列同类问题的某个解的情况，比如说：
题目：求一个数列中最大连续子序列的和。
我们要将这个原问题转化为：
状态定义：Fk是第k项前的最大序列和，求F1～FN中最大值。
通过换一种表述方式，我们清晰的发现了解决问题的思路，如何求出F1～FN中的最大值是解决原问题的关键部分。上述将原问题转化成另一种表述方式的过程叫做：状态的定义。这样的状态定义给出了一种类似通解的思路，把一个原来毫无头绪的问题转换成了可以求解的问题。
第二步：状态转移方程的定义 —————-递归地定义最优解的值（一个递推关系式）
在进行了状态的定义后，自然而然的想到去求解F1～FN中最大值。这也是状态定义的作用，让我们把一个总体的问题转化成一系列问题 ，而第二步：状态转移方程的定义则告诉我们如何去求解一个问题，对于上述已经转换成一系列问题我们要关注的点就在于：如何能够用前一项或者前几项的信息得到下一项，这种从最优子状态转换为下一个最优状态的思路就是动态规划的核心。
Fk=max{Fk-1+Ak,Ak}k是前k项的和，Ak是第k项的值
仔细思考一番，我们能够得到这样的结论，对于前k个项的最大子序列和是前k-1项的最大子序列和Fk与第k项的和、或者第k项两者中较大的。如果大家还是不能理解这个原理建议用演算纸自己计算一番，这里就不过多赘述了。这种状态转移的思路就是DP的核心。
第三步：计算最优解的值（目标函数的最大/小值） 动态规划是一种策略，不是一个具体的算法。
因此，动态规划求解不象搜索或数值计算，具有一个标准的数学表达式和明确清晰的解题方法。动态规划针对的最优化问题，由于问题性质的不同，确定最优解的条件的不同，动态规划的设计对不同的问题，有各具特色的解题方法。
改进一：若问题的决策序列由n次决策构成，而每次决策有p种选择，若采用枚举法，则可能的决策序列将有p^n^个。而利用动态规划策略的求解过程中仅保存了所有子问题的最优解，而舍去了所有不能导致问题最优解的次优决策序列，因此可能有多项式的计算复杂度。
改进二：重叠子问题性：动态规划与分治法也不同，分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则有些子问题被重复计算了很多次。动态规划保存了已解决的子问题的答案，在需要时找出已求得的答案，避免了大量的重复计算，节省了时间。
无论是采取自底向上还是自顶向下方法，动态规划分技术要点是：
用一个表（备忘）来记录所有已解的子问题的答案。
不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。
利用查表，避免对重复子问题的重复求解，动态规划可以将原来具有指数级复杂度的搜索算法改进成了具有多项式时间的算法，这是动态规划算法的根本目的。
关于动态规划求解代价的说明
在动态规划方法中，我们通常自底向上地使用最优子结构，即首先求子问题的最优解，然后求原问题的最优解。在求解原问题的过程中，需要在涉及的子问题中做出选择，选出能得到原问题最优解的子问题。这样，求解原问题的代价通常就是求子问题最优解的代价加上此次选择直接产生的代价 。
第四步：利用计算出的信息，构造一个最优解（求解向量） 动态规划的应用场景 看过了如何去使用动态规划，那么随之而来的问题就在于：既然动态规划不是某个固定的算法，而是一种策略思路，那么什么时候应该去使用什么时候不能用呢？答案很简短：
对于一个可拆分问题中存在可以由前若干项计算当前项的问题可以由动态规划计算。
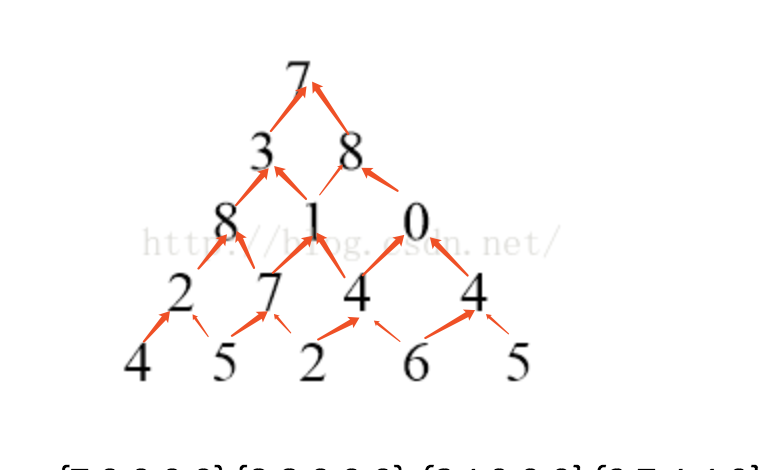
例题1: 数塔取数问题 一个高度为N的由正整数组成的三角形，从上走到下，求经过的数字和的最大值。
该三角形第n层有n个数字，例如：
第一层有一个数字： 5
第二层有两个数字： 8 4
第三层有三个数字： 3 6 9
第四层有四个数字：7 2 9 5
最优方案是：5 + 8 + 6 + 9 = 28
状态定义:分析：
（1）第一步：有底层向上层算起，因为这是一个金字塔的形状，底层向上算起，就可以最终到一个值，这个值就是最大值，
（2）每一层相加，然后比较取最大数。即：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import java.util.Scanner; public class Dp01 { public static void main (String[] args) { Scanner scan = new Scanner (System.in); int n = scan.nextInt(); long max = 0 ; int [][] dp = new int [n][n]; dp[0 ][0 ] = scan.nextInt(); for (int i=1 ;i<n;i++){ for (int j=0 ;j<=i;j++){ int num = scan.nextInt(); if (j==0 ){ dp[i][j] = dp[i-1 ][j] + num; }else { dp[i][j] = Math.max(dp[i-1 ][j-1 ],dp[i - 1 ][j])+num; } max = Math.max(dp[i][j],max); } } System.out.println(max); } }
例题2:编辑距离 编辑距离，又称Levenshtein距离（也叫做Edit Distance），是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。
状态定义:Fi,j表示第一个字符串的前i个字母和第二个字符串的前j个字母需要编辑的次数，求Fn,m，n和m分别是两个字符串的长度。
状态转移方程：
.
例题3:矩阵取数问题 一个N*N矩阵中有不同的正整数，经过这个格子，就能获得相应价值的奖励，从左上走到右下，只能向下向右走，求能够获得的最大价值。例如：3 * 3的方格。
1 3 3
能够获得的最大价值为：11。
我们必须注意到的一点是，到达一个格子的方式最多只有两种：从左边来的(除了第一列)和从上边来的(除了第一行)。因此为了求出到达当前格子的最短路径，我们就要先去考察那些能到达当前这个格子的格子，到达它们的最短路径。经过上面的分析，很容易可以得出问题的状态和状态转移方程。状态
其中i代表行，j代表列，下标均从0开始。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 public class MinPath { public static int getMin (int [][] map, int n, int m) { int [][] dp = new int [n][m]; for (int i=0 ;i<n;i++){ for (int j=0 ;j<=i;j++){ dp[i][0 ]+=map[j][0 ]; } } for (int i=0 ;i<m;i++){ for (int j=0 ;j<=i;j++){ dp[0 ][i]+=map[0 ][j]; } } for (int i=1 ;i<n;i++){ for (int j=1 ;j<m;j++){ dp[i][j] = min(dp[i][j-1 ]+map[i][j],dp[i-1 ][j]+map[i][j]); } } return dp[n-1 ][m-1 ]; } public static int min (int a,int b) { if (a>b){ return b; }else { return a; } } public static void main (String[] args) { Scanner sc=new Scanner (System.in); int m=sc.nextInt(); int n=sc.nextInt(); int map[][]=new int [m][n]; for (int i=0 ;i<m;i++){ for (int j=0 ;j<n;j++){ map[i][j]=sc.nextInt(); } } System.out.println(getMin(map,m,n)); }
例题4：钢条切割问题 给定一段长度为n英寸的长钢条和一个价格表P，求切割为短钢条的方案，使得销售收益rn最大。
长度i
1
2
3
4
5
6
7
8
9
10
价格pi
1
5
8
9
10
17
17
20
24
30
按价格从高到低分段出售，即先卖pi最大的段，然后再卖pj较小的段。是否可以获得最好的收益？（贪心策略）
对最优切割，设某次切割在位置i，将钢条分成长度为i和n-i的两段，令ri和rn-i分别是这两段的最优子切割收益，则有：rn=ri+ rn-i
钢条切割问题的朴素递归求解过程 基本思路:我们将钢条从左边切割下长度为i的一段，只对右边剩下的长度为n-i的一段继续进行切割(递归求解)，对左边的一段则不再进行切割。则可得公式：i为左边长度为i的钢条的收益，rn-i为右边长度为n-i的钢条继续切割后得到的最优收益，rn为长度为n的钢条切割后得到的最优收益。
但是此时，原问题的最优解只包含一个相关子问题（右端剩余部分）的解，而不是两个。就是分治的策略，会有很多重复计算在里面，所以效率不高。时间复杂度为O（2^n^）。
钢条切割问题的动态规划求解 带备忘录的自顶向下方法(top-down with memorization）
此方法仍然按照自然的递归形式编写过程，但过程中会保存每个子问题的解（通常是保存在数组或者散列表中），当需要一个子问题的解时，会先判断是否保存过此解。如果是，则直接返回保存的值，从而节省了计算时间。否则，按照常规方式进行计算。
因此，动态规划方法需要付出额外的空间保存子问题的解，是一种典型的时空权衡（time-memory trade-off）
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 public static int memorizedCutRod (int [] p, int n) { int result = 0 ; int res[] = new int [n+1 ]; for (int i = 0 ; i < res.length; i++) { res[i] = -1 ; } result = memorizedCutRodAux(p, n, res); return result; } public static int memorizedCutRodAux (int [] p, int n, int [] r) { if (r[n]>=0 ){ return r[n]; } int q = -1 ; if (n==0 ){ q = 0 ; } else { for (int i = 1 ;i<=n;i++){ q = Math.max(q, p[i]+memorizedCutRodAux(p, n-i, r)); } } r[n] = q; return q; }
自底向上的方法(bottom-up method)
这种方法一般需要恰当定义子问题的规模的概念，使得任何子问题的求解都只依赖于更小的子问题的求解。因而，我们可以将子问题按照规模排序，按照由小到大的顺序进行求解。当求解某个子问题时，它所依赖的那些更小的子问题都已经求解完毕，结果已经保存。每个子问题只需要求解一次，当我们求解它时，它的所有前提子问题都已经求解完成。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public static void extendedBottomUpCutRod (int [] p, int n) { int [] res = new int [n+1 ]; int [] solve = new int [n+1 ]; res[0 ] = 0 ; for (int i = 1 ; i <= n; i++) { int q = -1 ; for (int j = 1 ; j<=i;j++){ if (q<p[j]+res[i-j]){ q = p[j]+res[i-j]; solve[i] = j; } } res[i] = q; } print(res[n], solve, n); } public static void print (int maxValue, int [] solve, int n) { System.out.println(maxValue); while (n>0 ){ System.out.print(solve[n]+", " ); n = n - solve[n]; } }
具有相同的渐近运行时间：Θ(n^2^)
但由于自底向上法没有频繁的递归函数调用的开销，所以自底向上法的时间复杂性函数通常具有更小的系数。
而在某些特殊情况下，自顶向下法可能没有递归处理所有可能的子问题（剪枝）而减少工作量。
子问题图 在自底向上的动态规划方法中，对一个给定的子问题x，在求解它之前应先求解它所依赖的子问题。仅当它依赖的所有子问题都求解完成了，才会求解它。——这在子问题图中，对应顶点的一个逆拓扑序，可以按照深度优先原则进行处理。
基于子问题图“估算”算法的运行时间：
算法的运行时间等于所有子问题求解的时间之和。子问题图中，子问题对应顶点，子问题的数目等于顶点数。一个子问题的求解时间与子问题图中对应顶点的“出度”成正比。因此，一般情况下，动态规划算法的运行时间与顶点和边的数量至少呈线性关系。
问题五：矩阵链乘法 n个要连续相乘的矩阵构成一个矩阵链<A1,A2,…,An>,要计算这n个矩阵的连乘乘积：A1A2…An，称为矩阵链乘问题。
如，已知四个矩阵A1,A2,A3,A4，根据不同的加括号方式，乘积A1A2A3A4有五种不同的计算模式：(A1(A2(A3A4))) (A1((A2A3)A4)) ((A1A2)(A3A4)) ((A1(A2A3))A4)) ((A1A2)A3)A4)
两个矩阵A和B只有相容(compatible)，即A的列数等于B的行数时，才能相乘。如果A是p×q的矩阵，B是q×r的矩阵，那么乘积C是p×r的矩阵。计算C所需要时间由第8行的标量乘法的次数决定的，即pqr。
以矩阵链<A1,A2,A3>为例，来说明不同的加括号方式会导致不同的计算代价。假设三个矩阵的规模分别为10×100、100×5和5×50。100 5=5000次标量乘法，再与A3相乘又需要做105 50=2500次标量乘法，共需7500次标量乘法。5 50=25000次标量乘法，再与A1相乘又需10100 50=50000次标量乘法，共需75000次标量乘法。因此第一种顺序计算要比第二种顺序计算快10倍。
矩阵链乘法问题(matrix-chain multiplication problem)可描述如下：给定n个矩阵的链<A1,A2,…,An>，矩阵Ai的规模为p(i-1)×p(i) (1<=i<=n)，求完全括号化方案，使得计算乘积A1A2…An所需标量乘法次数最少。
因为括号方案的数量与n呈指数关系，所以通过暴力搜索穷尽所有可能的括号化方案来寻找最优方案是一个糟糕策略。
步骤一：最优括号化方案的结构特征 动态规划的第一步是寻找最优子结构，然后就可以利用这种子结构从子问题的最优解构造出原问题的最优解。在矩阵链乘法问题中，我们假设A(i)A(i+1)…A(j)的最优括号方案的分割点在A(k)和A(k+1)之间。那么，继续对“前缀”子链A(i)A(i+1)..A(k)，（记为Ai，k)进行括号化时，我们应该直接采用独立求解 它时所得的最优方案。k+1，j)的最优括号化问题)，求出子问题实例的最优解，然后将子问题的最优解组合起来 。我们必须保证在确定分割点时，已经考察了所有可能的划分点 ，这样就可以保证不会遗漏最优解。
步骤2：一个递归求解方案 对于矩阵链乘法问题，我们可以将对所有1<=i<=j<=n确定A(i)A(i+1)…A(j)的最小代价括号化方案作为子问题。令m[i,j]表示计算矩阵A(i..j)所需标量乘法次数的最小值，那么，原问题的最优解—**计算A(1..n)所需的最低代价就是m[1,n]**。
我们可以递归定义m[i,j]如下：m[i,j]就等于计算A(i..k)和A(k+1..j)的代价加上两者相乘的代价的最小值。 Ai,k是一个pi-1×pk的矩阵，Ak+1,j是一个pk×pj的矩阵。结果矩阵Ai,j是Ai,k和Ak+1,j最终相乘的结果。。因此，我们得到(i-1)p(k)p(j)
$$
$$
m[i,j]的值给出了子问题最优解的代价，但它并未提供足够的信息来构造最优解。为此，我们用s[i,j]保存最优括号化方案的分割点位置k，即使得 m[i,j]=m[i,k]+m[k+1,j]+ p(i-1)p(k)p(j)成立的k值。
步骤3：计算最优代价 我们采用自底向上表格法代替递归算法来计算最优代价。此过程假定矩阵Ai的规模为p(i-1)×pi(i=1,2,…,n)。它的输入是一个序列p=<p0,p1,…,pn>，其长度为p.length=n+1。过程用一个辅助表m[1..n,1..n]来保存代价m[i,j]，用另一个辅助表s[1..n-1,2..n]记录最优值m[i,j]对应的分割点k。我们就可以利用表s构造最优解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public static void PRINT_OPTIMAL_PARENS (int p[],int m[][M],int s[][M]) { int q,n=p.length()-1 ; for (int i=1 ;i<=n;i++)m[i][i]=0 ; for (int l=2 ;l<=n;l++) { for (int i=1 ;i<=n-l+1 ;i++) { int j=i+l-1 ; m[i][j]=100000 ; for (int k=i;k<=j-1 ;k++) { q=m[i][k]+m[k+1 ][j]+p[i-1 ]*p[k]*p[j]; if (q<m[i][j]) { m[i][j]=q; s[i][j]=k; } } } } }
步骤4：构造最优解 s[i,j]记录了AiAi+1…Aj的最优括号化方案中“首个”加括号的位置点k。
基于s[i,j]，对AiAi+1…Aj的括号化方案是：（AiAi+1…As[i,j]）（As[i,j]+1…Aj)
A1…n的最优方案中最后一次矩阵乘运算是：（A1…s[1,n]）（As[1,n]+1…n ）
1 2 3 4 5 6 7 8 9 10 11 12 public static void PRINT_OPTIMAL_PARENS (int s[][M],int i,int j) { if (i == j) System.out.println("A" ); else { System.out.println("(" ); PRINT_OPTIMAL_PARENS(s,i,s[i][j]); PRINT_OPTIMAL_PARENS(s,s[i][j]+1 ,j); System.out.println(")" ); } }
问题六：最长公共子序列LCS 两个字符串的最长公共非连续子串，称为最长公共子序列。
步骤一：LCS问题的最优子结构性 设A=“a0，a1，…，am”，B=“b0，b1，…，bn”，且Z=“z0，z1，…，zk”为它们的最长公共子序列。不难证明有以下性质：
步骤二：递推关系式
涵盖了步骤一中的所有情况。
步骤三：LCS的求解 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 public static int [][] longestCommonSubsequence(String str1, String str2) { int [][] c = new int [str1.length() + 1 ][str2.length() + 1 ]; char [][] b = new char [str1.length() + 1 ][str2.length() + 1 ]; for (int i = 0 ; i <= str1.length(); i++) { c[i][0 ] = 0 ; } for (int j = 0 ; j <= str2.length(); j++) { c[0 ][j] = 0 ; } for (int i = 1 ; i <= str1.length(); i++) { for (int j = 1 ; j <= str2.length(); j++) { if (str1.charAt(i - 1 ) == str2.charAt(j - 1 )) { c[i][j] = c[i - 1 ][j - 1 ] + 1 ; b[i][j]="↖" ; } else if (c[i-1 ,j]>=c[i,j-1 ]) { c[i][j] = c[i - 1 ][j]; b[i][j]="↑" ; } else if (c[i-1 ,j]<=c[i,j-1 ]) { c[i][j] = c[i][j-1 ]; b[i][j]="←" ; } } } return c; } }
说明：
c[i] [j]的含义是：x序列的前i个元素形成的子序列和y序列的前j个元素形成的子序列的最大公共子序列的值。
步骤四：构造出该LCS 由步骤三我们只是得出了LCS的长度，没有得出具体的LCS中的元素。
但是步骤三中得到了c这个二维数组，依照其元素的值：
反序，从b[m,n]处开始，沿箭头在表格中向上追踪。每当在表项b[i,j]中：
遇到一个“↖”时，意味着xi=yj是LCS的一个元素，下一步继续在b[i-1,j-1]中寻找上一个元素；
遇到“←”时，下一步到b[i,j-1]中寻找上一个元素；
遇到“↑”时，下一步到b[i-1,j]中寻找上一个元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public static void print (int [][] opt, String X, String Y, int i, int j) { if (i == 0 || j == 0 ) { return ; } if (X.charAt(i - 1 ) == Y.charAt(j - 1 )) { print(opt, X, Y, i - 1 , j - 1 ); System.out.print(X.charAt(i - 1 )); } else if (opt[i - 1 ][j] >= opt[i][j]) { print(opt, X, Y, i - 1 , j); } else { print(opt, X, Y, i, j - 1 ); } }
问题七：最优二叉搜索树（有点类似于树塔取数问题） 二叉搜索树（二分检索树）：
二叉搜索树Ｔ是一棵二元树，它或者为空，或者其每个结点含有一个可以比较大小的数据元素，且有：
Ｔ的左子树的所有元素比根结点中的元素小；
T的右子树的所有元素比根结点中的元素大；
Ｔ的左子树和右子树也是二叉搜索树。
不失一般性，这里假设所有元素互异
最优二叉搜索树的定义：
给定一个n个关键字的已排序的序列K=<k1,k2,…,kn>（不失一般性，设k1<k2<…<kn），对每个关键字ki，都有一个概率pi表示其被搜索的频率 。根据ki和pi构建一个二叉搜索树T，每个ki对应树中的一个结点。对搜索对象x，在T中可能找到、也可能找不到：
若x等于某个ki，则一定可以在T中找到结点ki，称为成功搜索。
成功搜索的情况一共有n种，分别是x恰好等于某个ki。
若x<k1 、或x>kn、或ki<x<ki+1 (1≤i<n), 则在T中搜索x将失败，称为失败搜索。
为此引入外部结点d0,d1,…,dn，用来表示不在K中的值,称为伪关键字。
伪关键字在T中对应外部结点，共有n+1个。——扩展二叉树：内结点表示关键字ki，外结点(叶子结点)表示di。
这里每个di代表一个区间。（d0表示所有小于k1的值，dn表示所有大于kn的值，对于i=1,…,n-1，di表示所有在ki和ki+1之间的值。）
**每个di也有一个概率qi**，表示搜索对象x恰好落入区间di的频率。
二叉搜索树的期望搜索代价：
对于特定搜索对象，搜索过程是从根开始到某个结点的检索过程。成功搜索结束于内结点，不成功搜索结束于外部结点。
记depthT(i)为结点i在T中的深度（根到i的路径上的边数）。则从根结点开始访问结点i的数量等于depthT(i) +1；
$$
即：加权平均代价，包括所有成功搜索的结点和失败搜索的结点。
对于给定的关键字及其概率集合，期望搜索代价最小的二叉搜索树称为其最优二叉搜索树。
问题：如何构造最优二叉搜索树？
步骤一：最优子结构
证明最优二叉搜索树的最优子结构：
如果T是一棵相对于关键字k1,…,kn和伪关键字d0,…,dn的最优二叉搜索树，则T中一棵包含关键字ki,…,kj的子树T’必然是相对于关键字ki,…,kj（和伪关键字di-1,…,dj）的最优二叉搜索子树。
我们可以利用最优二叉搜索树的最优子结构性来构造最优二叉搜索树。
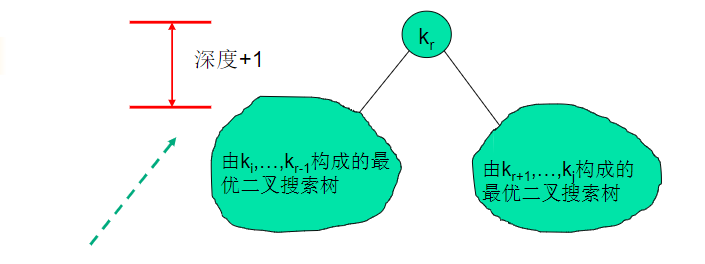
步骤二：递归算法的构建 对给定的关键字ki,…,kj，若其最优二叉搜索（子）树的根结点是kr（i≤r≤j），则kr的左子树中包含关键字ki,…,kr-1及伪关键字di-1,…,dr-1，右子树中将含关键字ki+1,…,kj及伪关键字dr,…,dj。
策略：在i≤l≤j的范围内检查所有可能的结点kl
(ki,ki+1,…,kj)的最优二叉搜索树，其中i>=1,j<=n且j>=i−1(当j=i−1时，子树不包含实际关键字，只包含伪关键字di−1).定义e[i,j]为包含关键字(ki,ki+1,…,kj)的二叉搜索树进行一次搜索的期望代价 ，最后我们希望求解得到e[1,n]。
当j = i - 1时，子树只有伪关键字di-1 ,所以，e[i,j]=qi-1
当j > = i时，从(ki,ki+1,…,kj)中选择根节点Kr
其左子树包含关键字(ki,ki+1,…,kr-1)且是最优二叉搜索子树
其右子树包含关键字(kr+1,kr+2,…,kj)且是最优二叉搜索子树
当一棵树成为另一个节点的子树时：
子树的所有结点的深度+1
根据搜索代价期望值计算公式，子树对根为kr的树的期望搜索代价的贡献是其期望搜索代价+其所含所有结点的概率之和。
所以，期望搜索代价增加量为：
原因：子树的每个结点的深度增加1。
所以若kr为包含关键字ki,ki+1,…,kj)的最优二叉搜索树的根，则其期望搜索代价e[i,j]与左、右子树的期望搜索代价e[i,r-1]和e[r+1,j]的递推关系为：
步骤三：计算二叉搜索树的期望搜素代价 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 private static int [][] Optimal_BST(double [] p, double [] q, int n) { double [][] e = new double [n+2 ][n+2 ]; double [][] w = new double [n+2 ][n+2 ]; int [][] root = new int [n+2 ][n+2 ]; for (int i=1 ;i<=n+1 ;i++){ e[i][i-1 ]=q[i-1 ]; w[i][i-1 ]=q[i-1 ]; } for (int l=1 ; l<=n ; l++){ for (int i=1 ;i<=n-l+1 ;i++){ int j=i+l-1 ; e[i][j]=Double.MAX_VALUE; w[i][j]=w[i][j-1 ]+p[j]+q[j]; for (int r=i;r<=j;r++){ double t = e[i][r-1 ]+e[r+1 ][j]+w[i][j]; if (t<e[i][j]){ e[i][j]=t; root[i][j]=r; } } } } return root; }
步骤四：构建最优解输出 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 CONSTRUCTOR-OPTIMAL-BST(root[][],i,j,r){ int rootChild = root[i][j]; if (rootChild == root[1 ][n]) { print("K" +rootChild+"是根" ); CONSTRUCTOR-OPTIMAL-BST(root,i,rootChild - 1 ,rootChild); CONSTRUCTOR-OPTIMAL-BST(root,rootChild + 1 ,j,rootChild); return ; } if (j < i - 1 ) { return ; } else if (j == i - 1 ) { if (j < r) { print( "d" + j + "是" + "k" + r + "的左孩子" ); } else { print( "d" + j + "是" + "k" + r + "的右孩子" ); } return ; } else { if (rootChild < r) { print ("k" + rootChild + "是" + "k" + r + "的左孩子" ); } else { print ("k" + rootChild + "是" + "k" + r + "的右孩子" ); } } CONSTRUCTOR-OPTIMAL-BST(root[],i,rootChild - 1 ,rootChild); CONSTRUCTOR-OPTIMAL-BST(root[],rootChild + 1 ,j,rootChild); }
问题八：01背包问题 https://blog.csdn.net/mu399/article/details/7722810?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
动态规划的具体实现 动态规划和递归 一个人爬楼梯，每次只能爬 1 个或 2 个台阶，假设有 n 个台阶，那么这个人有多少种不同的爬楼梯方法？
746. 使用最小花费爬楼梯 是这道题的换皮题， GrowingIO 前端工程师岗位考察过这个题目。
由于上第 n 级台阶一定是从 n - 1 或者 n - 2 来的，因此 上第 n 级台阶的数目就是 上 (n - 1) 级台阶的数目「加」上 (n - 2) 级台阶的数目。
递归代码：
1 2 3 4 5 function climbStairs (n) { if (n === 1 ) return 1 ; if (n === 2 ) return 2 ; return climbStairs (n - 1 ) + climbStairs (n - 2 ); }
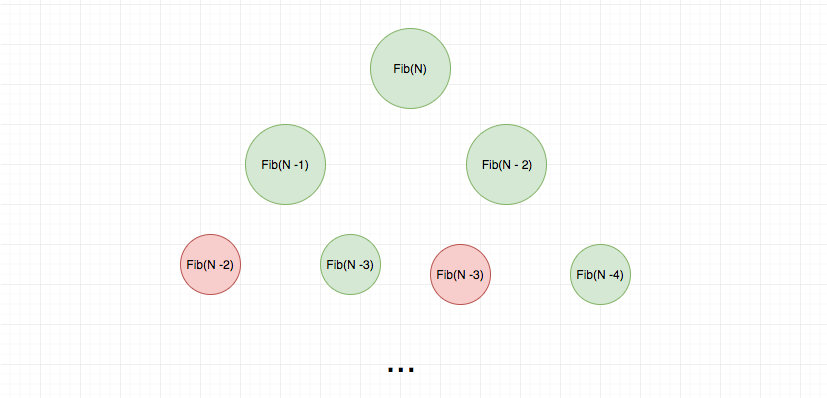
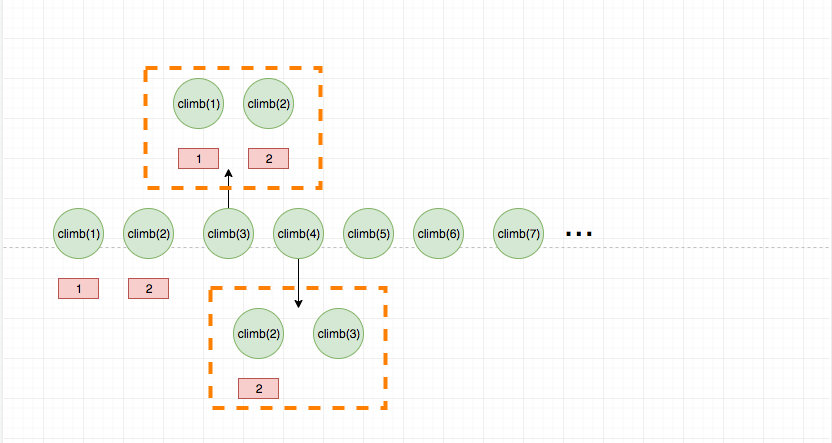
我们继续用一个递归树来直观感受以下：
红色表示重复的计算
可以看出这里面有很多重复计算，我们可以使用一个 hashtable 去缓存中间计算结果，从而省去不必要的计算。
那么动态规划是怎么解决这个问题呢？ 答案也是“查表”，不过区别于递归使用函数调用栈，动态规划通常使用的是 dp 数组，数组的索引通常是问题规模，值通常是递归函数的返回值。递归是从问题的结果倒推，直到问题的规模缩小到寻常。 动态规划是从寻常入手， 逐步扩大规模到最优子结构。
如果上面的爬楼梯问题，使用动态规划，代码是这样的：
1 2 3 4 5 6 7 8 9 10 11 function climbStairs (n) { if (n == 1) return 1 ; const dp = new Array (n); dp[0 ] = 1 ; dp[1 ] = 2 ; for (let i = 2 ; i < n; i++) { dp[i] = dp[i - 1 ] + dp[i - 2 ]; } return dp[dp.length - 1 ]; }
不会也没关系，我们将递归的代码稍微改造一下。其实就是将函数的名字改一下：
1 2 3 4 5 function dp (n) { if (n === 1 ) return 1 ; if (n === 2 ) return 2 ; return dp (n - 1 ) + dp (n - 2 ); }
dp[n] 和 dp(n) 对比看，这样是不是有点理解了呢? 只不过递归用调用栈枚举状态， 而动态规划使用迭代枚举状态。
动态规划的查表过程如果画成图，就是这样的：
虚线代表的是查表过程
这道题目是动态规划中最简单的问题了，因为只涉及到单个因素的变化，如果涉及到多个因素，就比较复杂了，比如著名的背包问题，挖金矿问题等。
对于单个因素的，我们最多只需要一个一维数组即可，对于如背包问题我们需要二维甚至更高维度的数组。
爬楼梯我们并没有必要使用一维数组，而是借助两个变量来实现的，空间复杂度是 O(1)。代码：
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 function climbStairs (n ) { if (n === 1 ) return 1 ; if (n === 2 ) return 2 ; let a = 1 ; let b = 2 ; let temp; for (let i = 3 ; i <= n; i++) { temp = a + b; a = b; b = temp; } return temp; }
之所以能这么做，是因为爬楼梯问题的状态转移方程中当前状态只和前两个状态有关 ，因此只需要存储这两个即可。 动态规划问题有很多这种讨巧的方式，这个技巧叫做滚动数组。
再次强调一下：
如果说递归是从问题的结果倒推，直到问题的规模缩小到寻常。 那么动态规划就是从寻常入手， 逐步扩大规模到最优子结构。
记忆化递归和动态规划没有本质不同。都是枚举状态，并根据状态直接的联系逐步推导求解。
动态规划性能通常更好。 一方面是递归的栈开销，一方面是滚动数组的技巧。
动态规划的三个要素
状态转移方程
临界条件
枚举状态
可以看出，用递归解决也是一样的思路
在上面讲解的爬楼梯问题中，如果我们用 f(n) 表示爬 n 级台阶有多少种方法的话，那么：
1 2 f (1 ) f (2 ) 就是【边界】f (n) f (n-1 ) + f (n-2 ) 就是【状态转移公式】
我用动态规划的形式表示一下：
1 2 dp 与 dp 就是【边界】 dp = dp + dp 就是【状态转移方程】
可以看出两者是多么的相似。
实际上临界条件相对简单，大家只有多刷几道题，里面就有感觉。困难的是找到状态转移方程和枚举状态。这两个核心点的都建立在已经抽象好了状态 的基础上。比如爬楼梯的问题，如果我们用 f(n) 表示爬 n 级台阶有多少种方法的话，那么 f(1), f(2), … 就是各个独立的状态 。
不过状态的定义都有特点的套路。 比如一个字符串的状态，通常是 dp[i] 表示字符串 s 以 i 结尾的 ….。 比如两个字符串的状态，通常是 dp[i][j] 表示字符串 s1 以 i 结尾，s2 以 j 结尾的 ….。
当然状态转移方程可能不止一个， 不同的转移方程对应的效率也可能大相径庭，这个就是比较玄学的话题了，需要大家在做题的过程中领悟。
搞定了状态的定义，那么我们来看下状态转移方程。
状态转移方程 爬楼梯问题由于上第 n 级台阶一定是从 n - 1 或者 n - 2 来的，因此 上第 n 级台阶的数目就是 上 (n - 1) 级台阶的数目「加」上 (n - 2) 级台阶的数目。
上面的这个理解是核心， 它就是我们的状态转移方程，用代码表示就是 f(n) = f(n - 1) + f(n - 2)。
实际操作的过程，有可能题目和爬楼梯一样直观，我们不难想到。也可能隐藏很深或者维度过高。 如果你实在想不到，可以尝试画图打开思路，这也是我刚学习动态规划时候的方法。当你做题量上去了，你的题感就会来，那个时候就可以不用画图了。
状态转移方程实在是没有什么灵丹妙药，不同的题目有不同的解法。状态转移方程同时也是解决动态规划问题中最最困难和关键的点，大家一定要多多练习，提高题感。接下来，我们来看下不那么困难，但是新手疑问比较多的问题 - 如何枚举状态 。
如何枚举状态 前面说了如何枚举状态，才能不重不漏是枚举状态的关键所在。
如果是一维状态，那么我们使用一层循环可以搞定。
如果是两维状态，那么我们使用两层循环可以搞定。
。。。
这样可以保证不重不漏。
但是实际操作的过程有很多细节比如:
一维状态我是先枚举左边的还是右边的？（从左到右遍历还是从右到左遍历）
二维状态我是先枚举左上边的还是右上的，还是左下的还是右下的？
里层循环和外层循环的位置关系（可以互换么）
。。。
其实这个东西和很多因素有关，很难总结出一个规律，而且我认为也完全没有必要去总结规律。不过这里我还是总结了一个关键点，那就是：
如果你没有使用滚动数组的技巧 ，那么遍历顺序取决于状态转移方程。比如:
1 2 for i in range(1 , n + 1 ): dp [i] = dp[i - 1 ] + 1 ;
那么我们就需要从左到右遍历，原因很简单，因为 dp[i] 依赖于 dp[i - 1]，因此计算 dp[i] 的时候， dp[i - 1] 需要已经计算好了。
二维的也是一样的，大家可以试试。
如果你使用了滚动数组的技巧 ，则怎么遍历都可以，但是不同的遍历意义通常不不同的。比如我将二维的压缩到了一维：
1 2 3 for i in range(1 , n + 1 ): for j in range(1 , n + 1 ): dp [j] = dp[j - 1 ] + 1 ;
这样是可以的。 dp[j - 1] 实际上指的是压缩前的 dp[i][j - 1]
而：
1 2 3 4 for i in range(1 , n + 1 ): for j in range(n, 0 , -1 ): dp [j] = dp[j - 1 ] + 1 ;
这样也是可以的。 但是 dp[j - 1] 实际上指的是压缩前的 dp[i - 1][j - 1]。因此实际中采用怎么样的遍历手段取决于题目。我特意写了一个 【完全背包问题】套路题（1449. 数位成本和为目标值的最大数字 文章，通过一个具体的例子告诉大家不同的遍历有什么实际不同，强烈建议大家看看，并顺手给个三连。
这个比较微妙，大家可以参考这篇文章理解一下 0518.coin-change-2 。
小结 关于如何确定临界条件通常是比较简单的，多做几个题就可以快速掌握。
关于如何确定状态转移方程，这个其实比较困难。 不过所幸的是，这些套路性比较强， 比如一个字符串的状态，通常是 dp[i] 表示字符串 s 以 i 结尾的 ….。 比如两个字符串的状态，通常是 dp[i][j] 表示字符串 s1 以 i 结尾，s2 以 j 结尾的 ….。 这样遇到新的题目可以往上套， 实在套不出那就先老实画图，不断观察，提高题感。
关于如何枚举状态，如果没有滚动数组， 那么根据转移方程决定如何枚举即可。 如果用了滚动数组，那么要注意压缩后和压缩前的 dp 对应关系即可。
动态规划为什么要画表格 动态规划问题要画表格，但是有的人不知道为什么要画，就觉得这个是必然的，必要要画表格才是动态规划。
其实动态规划本质上是将大问题转化为小问题，然后大问题的解是和小问题有关联的，换句话说大问题可以由小问题进行计算得到。这一点是和用递归解决一样的， 但是动态规划是一种类似查表的方法来缩短时间复杂度和空间复杂度。
画表格的目的就是去不断推导，完成状态转移， 表格中的每一个 cell 都是一个小问题， 我们填表的过程其实就是在解决问题的过程，
我们先解决规模为寻常的情况，然后根据这个结果逐步推导，通常情况下，表格的右下角是问题的最大的规模，也就是我们想要求解的规模。
比如我们用动态规划解决背包问题， 其实就是在不断根据之前的小问题A[i - 1][j] A[i -1][w - wj]来询问：
至于判断的标准很简单，就是价值最大，因此我们要做的就是对于选择和不选择两种情况分别求价值，然后取最大，最后更新 cell 即可。
其实大部分的动态规划问题套路都是“选择”或者“不选择”，也就是说是一种“选择题”。 并且大多数动态规划题目还伴随着空间的优化（滚动数组），这是动态规划相对于传统的记忆化递归优势的地方。除了这点优势，就是上文提到的使用动态规划可以减少递归产生的函数调用栈，因此性能上更好。
Leetcode 5.最长回文子串
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution { public String longestPalindrome (String s) { int len = s.length(); if (len<=1 )return s; char []chars = s.toCharArray(); int maxLen = 1 ; int begin = 0 ; boolean [][] dp = new boolean [len][len]; for (int i=0 ;i<len;i++) { if (i+1 <len)dp[i][i+1 ]=true ; dp[i][i]=true ; } for (int j=1 ;j<len;j++) for (int i=0 ;i<j;i++) { if (chars[i]!=chars[j]) dp[i][j]=false ; else { if (j-i<3 ) dp[i][j]=true ; else dp[i][j]=dp[i+1 ][j-1 ]; } if (dp[i][j]==true &&maxLen<j-i+1 ) { maxLen=j-i+1 ;begin=i; } } return s.substring(begin,begin+maxLen); } }
略
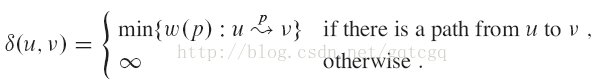
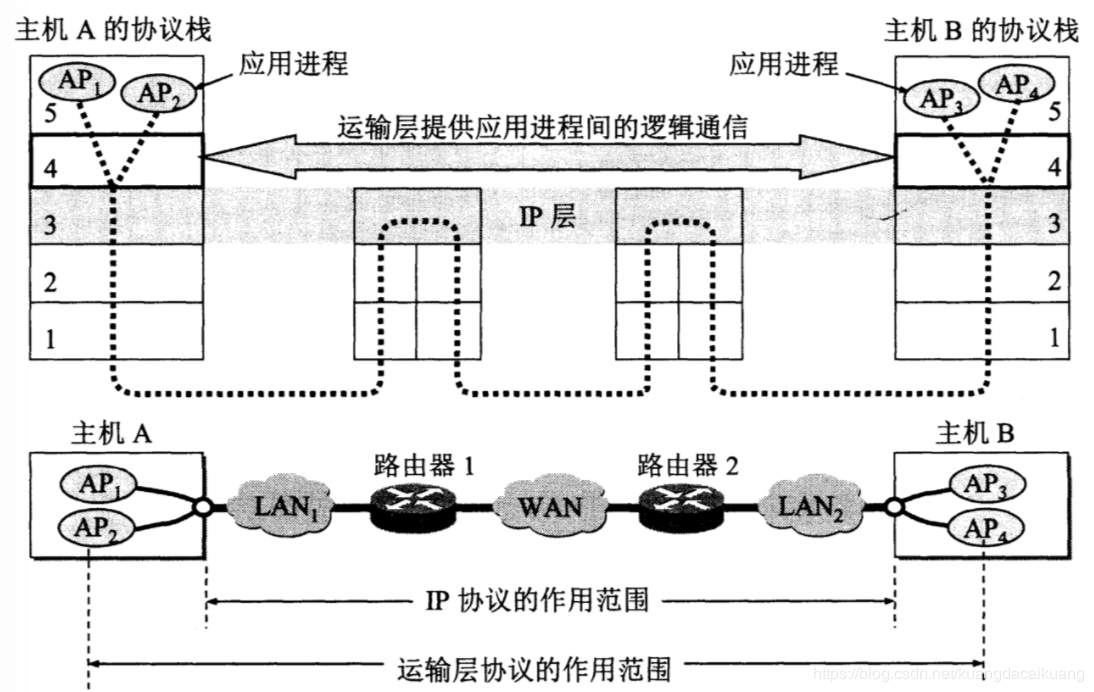
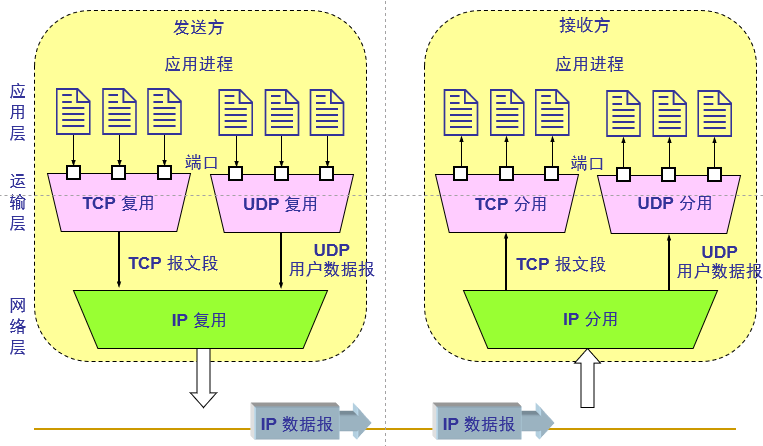
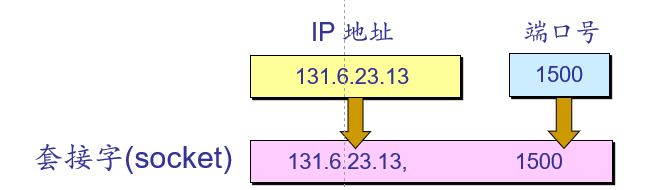
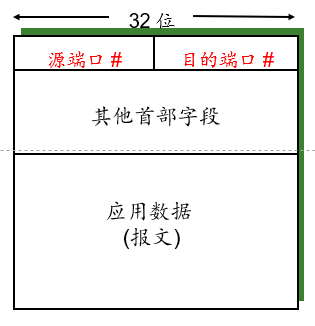
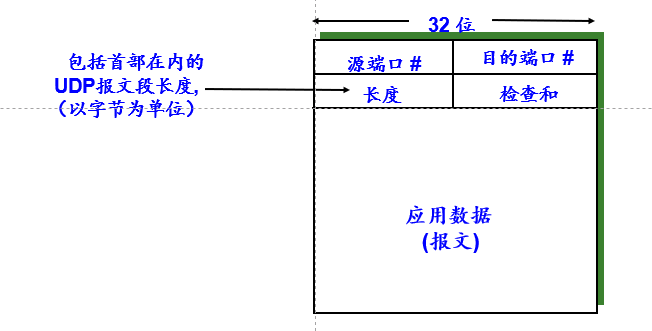
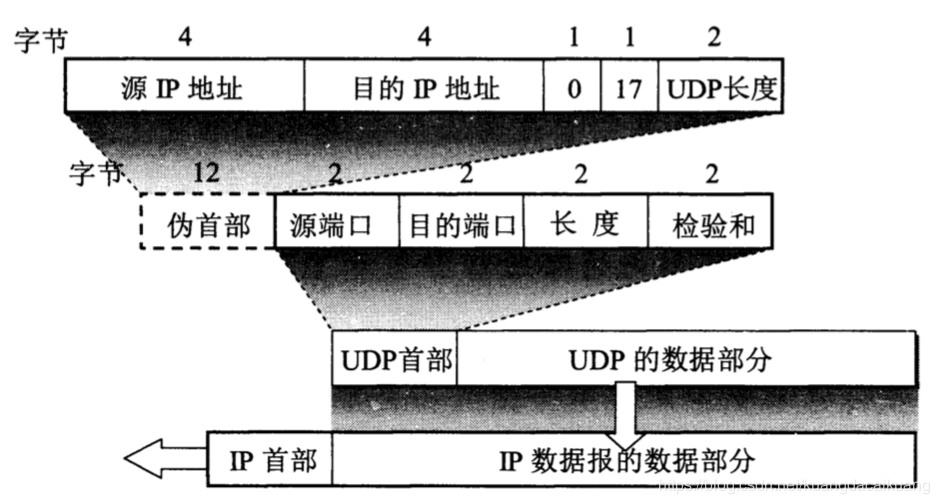
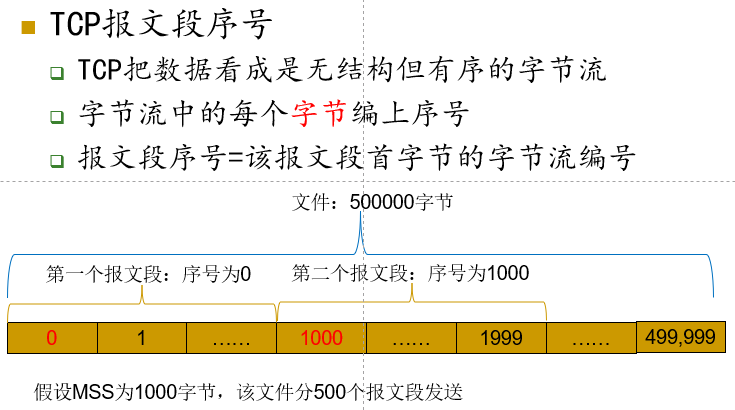
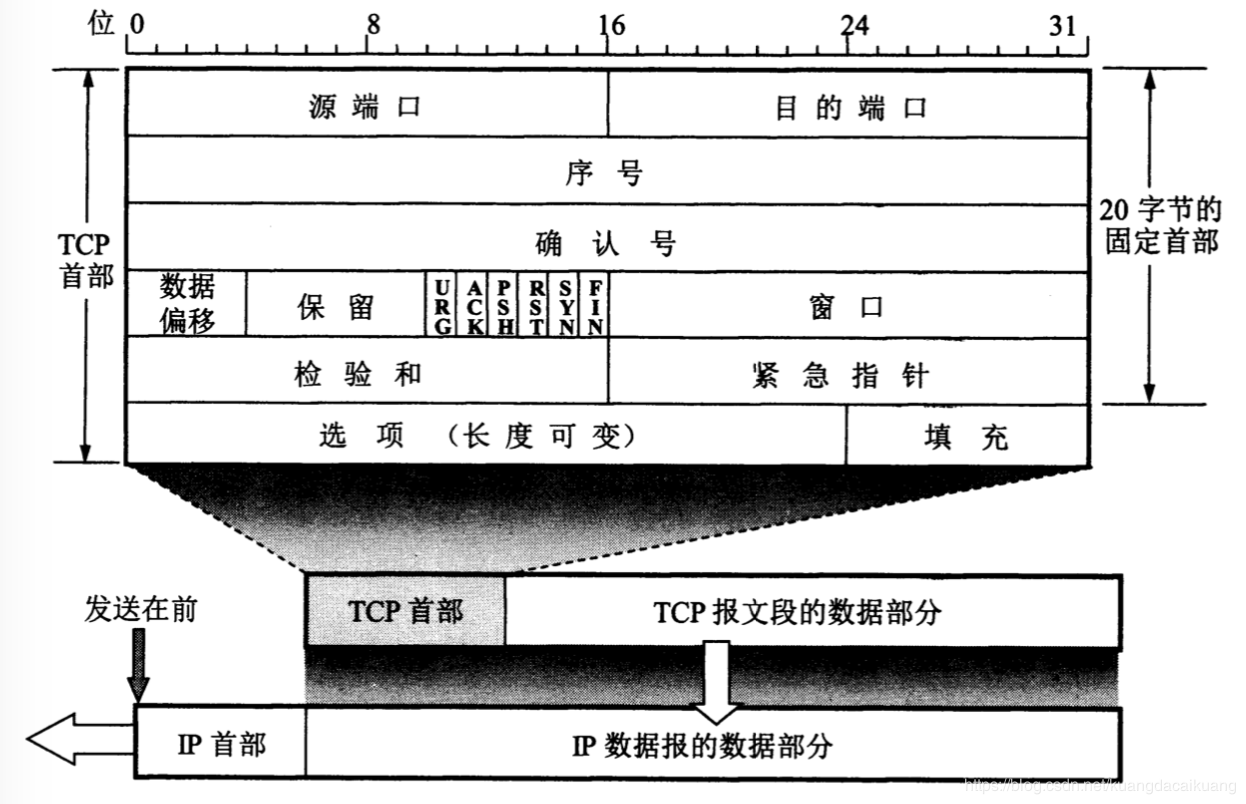源端口和目的端口 : 各占两个字节.
