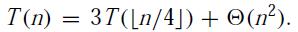rhb_blog

rao的博客

0%

发表于 更新于 分类于 ，

输入输出系统

概述

IO系统具有的特点

  • 异步性：外围设备相对于处理机是异步工作的。
  • 实时性：当外围设备与处理机交互时，由于设备的类型不同，它们的工作步调是不同的，处理机必须按照不同设备所要求传送方式和传输速率不失时机地为设备提供服务，这就要求实时性控制；
  • 与设备无关性：各种外部设备必须根据其特点和要求选择一种标准接口和处理机进行连接，它们之间的差别必须由设备本身的控制器通过硬件和软件来填补；这样，处理机本身无须了解外设的具体细节，可以采用统一的硬件和软件对其管理。

输入过程

1、CPU将一个地址放在地址总线上，选择设备

2、CPU等候输入设备的数据成为有效

3、CPU从数据总线读入数据

输出过程

1、CPU将一个地址放在地址总线上，选择设备

2、CPU把数据放在数据总线上；

3、输出设备认为数据有效，取走数据

输入输出方式

  • 无条件IO方式难做到

在程序的适当位置直接安排I/O指令，当程序执行到这些I/O指令时，CPU默认外设始终是准备就绪的（I/O总是准备好接收CPU的输出数据，或总是准备好向CPU输入数据），无需检查I/O的状态，就进行数据的传输；

硬件接口电路和软件控制程序都比较简单。输入时，必须确保CPU执行I/O指令读取数据时，外设已将数据准备好；输出时，必须确保外部设备的数据锁存器为空，即外设已将上次的数据取走，等待接收新的数据，否则会导致数据传送出错，但一般的外设难以满足这种要求。

  • 程序控制IO方式

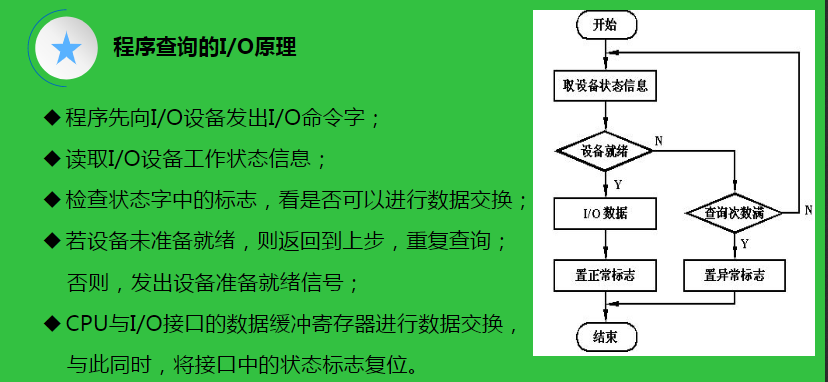
如果不设置查询次数，就可能会无限次循环导致死机。

设备状态字寄存器：

  1. 用来标志设备的工作状态，以便接口对外部设备进行监视。
  2. CPU通过程序查询设备状态位来判断设备的状态。
  3. 因此，设备状态寄存器是设备对主机的窗口，主机通过它了解设备的状态，并对设备设置操作方式。
  4. 设备状态寄存器又叫设备状态字（DSW）是设备所有状态的集合，每种状态均用一个触发器来表示。

程序控制I/O方式特点：何时对何设备进行输入输出操作完全受CPU控制，外围设备与CPU处于异步工作关系，数据的输入/输出都要经过CPU。

  • 中断IO方式

当外设准备好后，主动通知CPU并进行接收或输出数据的方法；

CPU接到外设的通知后暂停现行的工作，转入中断服务程序，和外设交换数据，等中断程序处理完毕后，再返回到被中断的原程序中继续以前被暂停的工作。

  • DMA

是一种完全由硬件执行的I/O交换方式

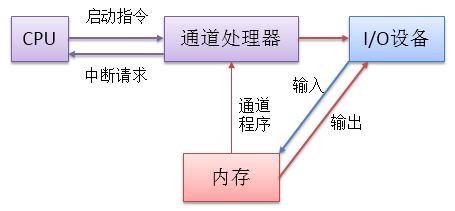
  • 通道方式和IO处理机方式

在复杂的计算机系统中，外围设备的台数一般比较多，设备的种类、工作方式和工作速度的差别很大，为了把对外围设备的管理工作从CPU中分离出来，采用通道或I/O处理机方式。

通道是能够专门执行I/O指令的处理机，它可以实现对外围设备的统一管理，以及外设与主存之间的数据传输。

（通道可以跑简单的IO程序）

I/O处理机是通道方式的进一步发展，它的结构更接近于一般处理机。

中断请求和响应

可以实现主机和外设之间的并行工作。

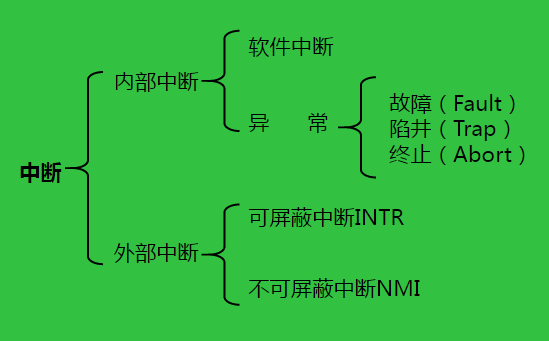
中断的类型

内部中断：来自于CPU内部的指令中断请求，分为软件中断和异常。

外部中断：中断请求来自CPU外部，又分为可屏蔽和不可屏蔽中断。

不可屏蔽中断NMI：由系统内部硬件引发的中断，优先级高于外部硬件中断，且不受中断允许标志位的影响，所以是不可屏蔽中断。

可屏蔽中断：由外设通过中断请求线向处理器申请而产生的中断，处理器可以用指令来屏蔽（禁止），即不响应它的中断请求。

中断的基本功能

中断请求信号保持与清除

使用硬件方式实现

中断源识别

识别中断号。

中断控制

中断触发方式：是指外设以什么逻辑信号去申请中断，即边沿触发和电平触发两种方式。

中断排队方式：当系统有多个中断源时，就可能出现同时有几个中断源都申请中断，而处理器在一个时刻只能响应并处理一个中断请求；为此，要进行中断排队。处理器按“优先级高的先服务”的原则提供服务。

  • 按优先级排队：根据任务的轻重缓急，给每个中断源指定CPU响应的优先级，任务紧急的先响应，可以暂缓的后响应。
  • 循环轮流排队：不分级别高低，CPU轮流响应各个中断源的中断请求。

中断嵌套

当CPU正在处理某个中断时，会出现优先级更高的中断源申请中断；为了使更紧急的、级别更高的中断源及时得到服务，需要暂时打断（挂起）当前正在执行的中断服务程序，去处理级别更高的中断请求，处理完成后再返回被打断了的中断服务程序继续执行。

但级别相同或级别低的中断源不能打断级别高的中断服务，这就是所谓的中断嵌套。

可屏蔽中断可以进行中断嵌套。NMI不可以进行中断嵌套。

中断屏蔽

处理器用指令来控制中断屏蔽触发器的状态，从而控制是否接受某个特殊外设的中断请求。

处理器内部也有一个中断允许触发器，只有当其为“1”（即开中断），CPU才能响应外部中断。

中断优先级

硬件响应优先序：未被屏蔽的几个中断源同时提出申请时，CPU选择服务对象的顺序由硬件电路实现，用户不能修改。

  • 响应优先序是指CPU对设备中断请求进行响应的先后次序

软件服务优先序：在各中断服务程序开头，用软件设置自己的中断屏蔽字，以此改变实际服务顺序。

  • 服务优先序是指CPU实际完成中断处理程序的先后次序

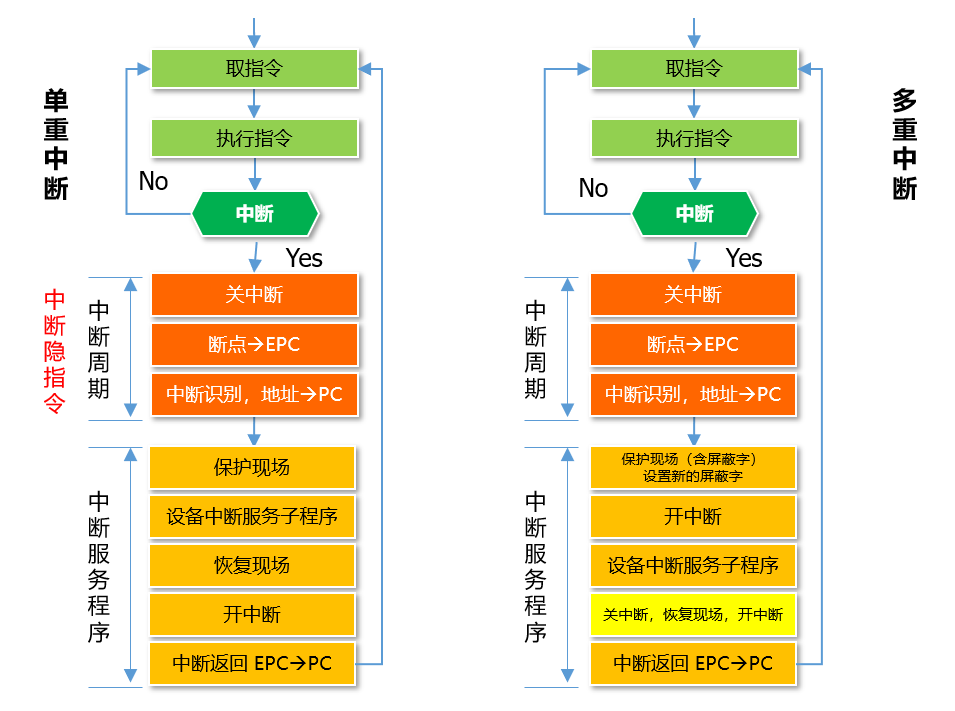
中断的处理

注意多重中断处理流程。

DMA

DMA的设计是为了解决中断处理程序中每次传送一个字节、字就要响应中断的麻烦。

方式：

  • 外设与主存间建立一个由硬件管理的数据通路
  • CPU不介入外设与主存的数据传送操作
  • 减少CPU开销，提升效率

通常系统总线是由CPU管理的，在ＤＭＡ方式时，就希望CPU把这些总线让出来，即CPU连到这些总线上的线处于第三态(高阻状态)，而由DMA控制器接管，控制传送的字节数，判断DMA是否结束，以及发出DMA结束信号。因此DMA控制器必须有以下功能:

1、能向CPU发出系统保持(HOLD)信号，提出总线接管请求；

2、当CPU发出允许接管信号后，负责对总线的控制，进入DMA方式;

3、能对存储器寻址及能修改地址指针，实现对内存的读写；

4、能决定本次DMA传送的字节数，判断DMA传送是否借宿。

5、发出DMA结束信号，使CPU恢复正常工作状态。

DMA传输将从一个地址空间复制到另外一个地址空间。当CPU初始化这个传输动作，传输动作本身是由DMA控制器来实行和完成。 典型例子—移动一个外部内存的区块到芯片内部更快的内存区。

对于实现ＤＭＡ传输，它是由DMA控制器直接掌管总线（地址总线、数据总线和控制总线），因此，存在一个总线控制权转移问题

DMA传输开始前：　　　　CPU——>DMA控制器

DMA传输结束后： DMA控制器——>CPU

一个完整的DMA传输过程必须经历DMA请求、DMA响应、DMA传输、DMA结束4个步骤。

DMA方式是一种完全由硬件进行组信息传送的控制方式，具有中断方式的优点，即在数据准备阶段，CPU与外设并行工作。

DMA传输步骤

申请阶段：一个设备接口试图通过总线直接向另一个设备发送数据(一般是大批量的数据)，它会先向CPU发送DMA请求信号；

响应阶段：CPU收到DMA请求信号后，在当前的总线周期结束后，会按DMA信号的优先级和提出DMA请求的先后顺序响应DMA信号；

数据传送阶段：CPU对某个设备接口响应DMA请求时，会让出总线控制权；于是在DMA控制器的管理下，外设和存储器直接进行数据交换，而不需CPU干预；

传送结束阶段：数据传送完毕后，设备接口会向CPU发送DMA结束信号，交还总线控制权。

DMA传输模式

停止CPU访问内存

当需要传送一批数据时，DMA控制器首先要求CPU放弃对总线的控制权；然后开始进行数据传送。在一批数据传送完毕后，DMA控制器通知CPU可以使用内存，并把总线控制权交还给CPU。在这种DMA传送过程中，CPU基本处于不工作状态或者说保持状态。

周期挪用

停止CPU访问内存会导致内存使用效率不高。

当I/O设备没有DMA请求时，CPU按程序要求访问内存；一旦I/O设备有DMA请求，则由I/O设备挪用一个或几个内存周期。

DMA要求访问主存时，CPU暂停一个或多个存储周期。一个数据传送结束后，CPU继续运行。

CPU现场没有变动，仅延缓了指令的执行

I/O设备要求DMA传送时可能遇到两种情况：

  • 当CPU不需要访问内存时，此时I/O访内与CPU访内没有冲突，即I/O设备挪用一二个内存周期对CPU执行程序没有任何影响；
  • CPU也同时要求访问内存，这就产生了访存冲突，在这种情况下I/O设备访存优先。

DMA和CPU交替访问内存

如果CPU的工作周期比内存存取周期长很多，此时采用交替访存的方法，可以使DMA传送和CPU同时发挥最高的效率。

将主存的存取周期分成两段：一段给CPU使用，一段给DMAC使用。

缺点是硬件的代价很大，会很复杂。

DMA和中断的区别

  1. 中断通过程序传送数据，DMA靠硬件来实现。
  2. 中断时机为两指令之间，DMA响应时机为两存储周期之间。
  3. 中断不仅具有数据传送能力，还能处理异常事件。DMA只能进行数据传送。
  4. DMA仅挪用了一个存储周期，不改变CPU现场。
  5. DMA请求的优先权比中断请求高。CPU优先响应DMA请求，是为了避免DMA所连接的高速外设丢失数据。
  6. DMA利用了中断技术

通道方式

DMA方式依赖硬件逻辑支持，随着设备数量的增加，DMA控制器增加，成本也相应增加。

设置专用的输入输出处理机（通道），分担输入输出管理的全部或大部分工作。

吸取了DMA技术，增加了软件管理，设有专用通道指令

层次性的I/O系统

  • 一个主机可以连接多个通道
  • 一个通道可以管理多个设备控制器
  • 一个设备控制器又可以控制多台设备。

⑴字节多路通道
　　它适用于连接打印机、终端等低速或中速的I/O设备。这种通道以字节为单位交叉工作：当为一台设备传送一个字节后，立即转去为另一它设备传送一个字节。

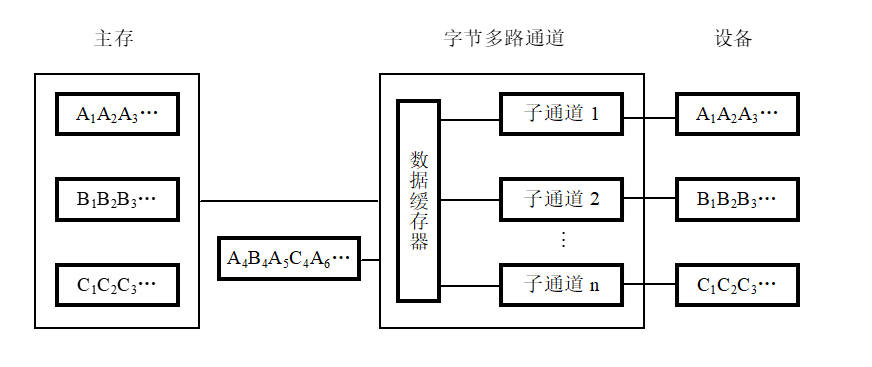
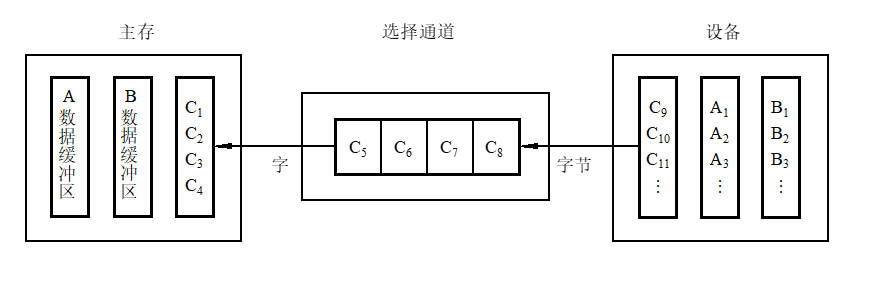
⑵选择通道
　　它适用于连接磁盘、磁带等高速设备。这种通道以“组方式”工作，每次传送一批数据，传送速率很高，但在一段时间只能为一台设备服务。每当一个I/O请求处理完之后，就选择另一台设备并为其服务。

⑶成组多路通道
　　这种通道综合了字节多路通道分时工作和选择通道传输速率高的特点，其实质是：对通道程序采用多道程序设计技术，使得与通道连接的设备可以并行工作。

  • 多个设备以数据组（块）为单位交叉使用通道。
  • 设备占用通道时，连续传送一组数据，然后将出让通道使用权
  • 数据组的大小因设备而异，有256B、512B或1KB等。

通道控制方式与DMA控制方式的区别

1）DMA控制方式中需要CPU来控制所传输数据块的大小，传输的内存地址；通道控制方式中这些信息都是由通道来控制管理的。

2）一个DMA控制器对应一台设备与内存传递数据，而一个通道可以控制多台设备与内存的数据交换。

—– I/O通道与一般处理器的区别：I/O通道的指令类型单一，其所能执行的命令主要局限于与I/O操作有关的指令；通道没有自己的内存，通道所执行的通道程序放在主机的内存中，也就是说通道是与CPU共享内存的。

PS

名词解释

(1)接口：接口是两个不同部件或系统之间的连接部分，可以是两个硬设备(可以都是计算机，也可以都是外部设备)之间的连接，也可以是软件系统中两个独立程序块之间的连接。

(2)中断：计算机系统运行时，若系统外部、内部或现行程序本身出现某种非预期的事件，CPU将暂时停下现行程序，转向为该事件服务，待事件处理完毕，再恢复执行原来被终止的程序，这个过程称为中断。

(3) 中断处理优先级:处理优先级是指CPU实际完成中断处理程序的先后次序。对单级中断而言,先被CPU响应的中断服务程序先完成；对多重中断而言，先被CPU响应的中断不一定先完成，这与中断屏蔽密切相关。

(4) 中断屏蔽: 为了便于利用程序控制中断处理的先后顺序，可通过程序有选择地封锁部分中断源发出的中断请求，而允许其余部分中断仍得到响应，这种方式称为中断屏蔽。

(5) 多重中断: 若在中断服务程序执行过程中，如果允许CPU响应其它中断请求，则这种中断称为多重中断，也称中断嵌套。

(6) 中断向量: 通常将中断服务程序的入口地址和程序状态字(有的机器不包含此项)称为中断向量。

(7) 中断响应优先级: 响应优先级是指CPU对各设备中断请求进行响应的先后次序，它根据中断事件的重要性和迫切性而定。当几个设备同时有中断请求时，优先级高的先响应，优先级低的后响应。

(8) 中断隐指令: CPU响应中断之后，经过某些操作，转去执行中断服务程序。这些操作是由硬件直接实现的，把它称为中断隐指令。中断隐指令并不是指令系统中的一条真正的指令，它没有操作码，所以中断隐指令是一种不允许、也不可能为用户使用的特殊指令。

(9) 程序中断I/O: 当主机启动外设后，无需等待查询，而是继续执行原来的程序，外设在做好输入输出准备时，向主机发出中断请求，主机接到请求后就暂时中止原来执行的程序，转去执行中断服务程序对外部请求进行处理，在中断处理完毕后返回原来的程序继续执行。

(10)程序查询I/O: 程序查询方式是一种程序直接控制方式,这是主机与外设间进行信息交换的最简单的方式,输入和输出完全是通过CPU执行程序来完成的。一旦某一外设被选中并启动后，主机将查询这个外设的某些状态位，看其是否准备就绪？若外设未准备就绪，主机将再次查询；若外设已准备就绪，则执行一次I/O操作。

(11)DMA: 直接存储器存取控制方式DMA方式下外设与主存之间传送数据时，CPU仍可执行主程序.

(12)周期挪用:周期挪用是指利用CPU不访问存储器的那些周期来实现DMA操作，此时DMAC可以使用总线而不用通知CPU也不会妨碍CPU的工作。

(13)通道: 通道方式是DMA方式的发展，在通道方式下，数据的传送方向、存取数据的内存起始地址及传送的数据块长度等都由独立于CPU的通道来进行控制，因此，通道方式可进一步减少CPU的干预。

(14)选择型通道: 对于这种高速传输，通道难以同时对多个这样的设备进行操作，只能一次对一个设备进行操作,这种通道称为选择通道。

(15)通道指令: 通道程序是由一系列通道指令组成的，通道指令一般包含被交换数据在内存中应占据的位置、传送方向、数据块长度及被控制的I/O设备的地址信息、特征信息（例如是磁带设备还是磁盘设备）等.

(16)输入设备:向计算机输入数据和信息的设备.

(17)输出设备:是人与计算机交互的一种部件，用于数据的输出。

(18)显示分辨率:显示分辨率是显示器在显示图像时的分辨率，分辨率是用点来衡量的，显示器上这个“点”就是指像素(pixel)。

(19)点距: 点距指屏幕上相邻两个同色像素单元之间的距离，即两个红色（或绿、蓝）像素单元之间的距离。

(20)行反转扫描法: 先对所有行线送”1”，所有列线送“0”，读键盘行扫描值；然后反过先对所有行线送”0”，然后对所有列线送“1”，并读键盘列扫描值。

简要问题

1)什么是接口?它有哪些功能?

2)主机与外部设备之间如何连接?

3)主机与外部设备信息交换的控制方式有哪些?各有什么特点?

4)什么是程序程序查询I/O方式,简要说明其工作原理.

5)比较单级中断和多重中断处理流程的异同点.

6)中断隐指令完成什么功能?

7)为什么在保护现场和恢复现场的过程中,CPU必须关中断?

8)CPU响应中断的条件有哪些?

9)什么是中断向量,简要分析中断向量方式下形成中断向量的基本方法.

10)为什么采用DMA方式能提高成组数据传送的速度?

11)什么是中断优先级?它具有哪两层含义?划分优先等级的原则是什么?

12)计算机中断系统中使用屏蔽技术有什么好处?

13)计算机中断响应后，如何调出中断服务程序?

14)DMA方式传送数据前，主机应向DMA接口输送哪些参数?

15)比较中断I/O和DMA的一统点。

16)比较DMA与通道的异同点。

17)中断系统中设计中断允许和中断屏蔽的作用分别是什么?两者是否可以合二为一?

解：(1)接口是两个不同部件或系统之间的连接部分，可以是两个硬设备(可以都是计算机，也可以都是外部设备)之间的连接，也可以是软件系统中两个独立程序块之间的连接。

具有的功能：1)寻址功能。2)数据输入/输出功能。3)匹配主机与外设的速度差距。4)实现数据格式转换或逻辑电平转换。5)传送主机命令。6)反映设备的工作状态。

(2)主机通过接口连接I/O设备，接口实现主机与外设的连接和信息的交换。

(3) 主机与外部设备信息交换的控制方式有:程序查询控制方式、程序中断控制方式、直接存储器存取控制方式(DMA)、通道方式、外围处理机方式。

特点：程序查询控制方式接口设计简单，但是CPU与外设只能串行工作，由于CPU的速度比外设的速度要高得多，所以在信息传送过程中，CPU的大量时间是花费在查询和等待上，从而使系统效率大大降低。

程序中断控制方式：允许外部设备用“中断”信号中止CPU正在执行的程序。具体他说，当接口电路需要与CPU进行数据交换（输入、输出等）时，便由接口电路向CPU发出一个中断请求信号，CPU响应这一中断请求，并调用中断服务程序完成一个或多个字节的信息交换。这种方式不需要接口软件主动查询，而是由接口电路主动通知CPU，即在设备准备数据阶段，CPU与外设能并行工作，使得接口软件的效率比较高。

直接存储器存取控制方式：数据传输的基本单位是数据块；所传输的数据是从设备直接送入内存的,或者相反；整块数据的传送是在控制器的控制下完成的；

通道方式：CPU发出启动通道的指令，通道就开始工作。I/O通道控制I/O控制器工作，I/O控制器又控制I/O设备。这样，一个通道可以连接多个I/O控制器，而一个I/O控制器又可以连接若干台同类型的外部设备。

外围处理机方式: 通常用于大、中型计算机系统中。由于PPU基本上独立于主机工作，其结构更接近一般处理机，甚至就是一般的通用微小型计算机。它可以完成IOP的功能，还可以完成码制变换、格式处理、数据块检错、纠错等操作。

发表于 更新于 分类于 ，

分治策略

分治法遵循三个基本步骤：

1）分解（Divide）：将原问题分为若干个规模较小、相互独立，性质与原问题一样的子问题；

2）解决（Conquer）：若子问题规模较小、可直接求解时则直接解；否则“递归”求解各个子问题，即继续将较大子问题分解为更小的子问题，然后用同一策略继续求解子问题。

3）合并（Combine）：将子问题的解合并成原问题的解。

递归式求解的三种方法

通常遇到的输入规模为n的递归式，形式如下：

$$T(n) = aT(n/b) + f(n)$$

该式描述的是：它将规模为n的问题分解为a个子问题，每个子问题规模为n/b，其中a和b都是正常数。a个子问题递归地进行求解，每个花费时间T(n/b)。函数f(n)包含了问题分解和子问题解合并的代价。例如，描述Strassen算法的递归式中，a=7，b=2，f(n) = Θ(n2) 。

接下来分析求解上述式子的三种方法

代入法

实质上就是数学归纳法，先对一个小的值做假设，然后推测更大的值得正确性。

​ 1.猜测解的形式；

​ 2.用数学归纳法求出解中的常数，并证明解是正确的。

示例

T(n) = 2T(n/2) + n

  • step one: 猜测
    上述等式可以转换为 T(n)/n = 2T(n/2)/n + 1
    令 S(n) = T(n)/n
    则S(n) = S(n/2) + 1
    而这种形式与以下的等式很像(这是关键步骤)
    lgn = lg (n/2) + 1 (此处lg2 = 1)
    因此可以推测 T(n) / n = clgn (c是常数)

因此猜出其解为 T(n) = O(nlgn)

  • step two: 数学归纳法证明这个解的合理性
    直接代入去运算

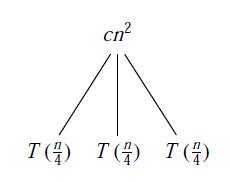
递归树法

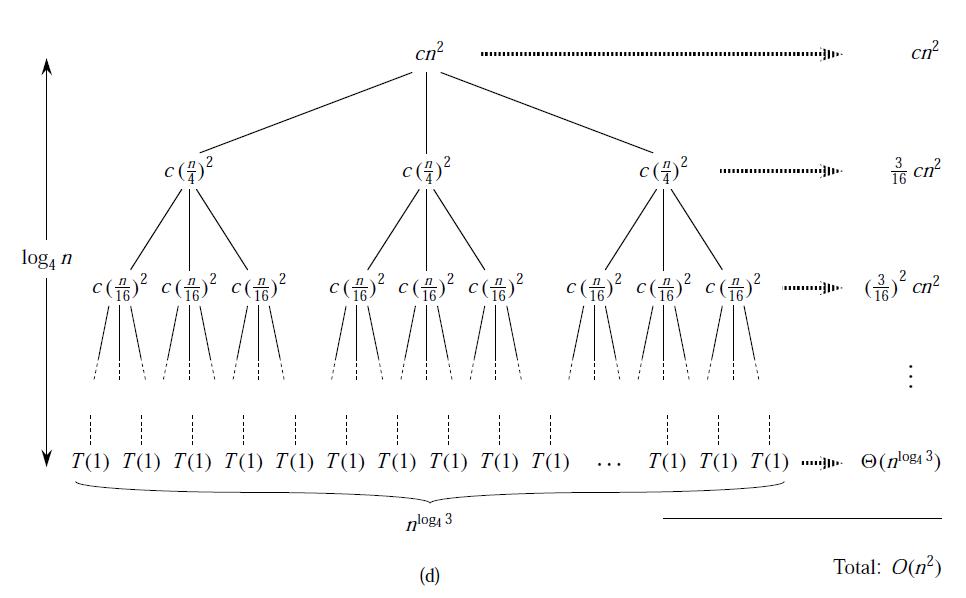
利用递归树方法求算法复杂度，其实是提供了一个好的猜测，简单而直观。在递归树中，每一个结点表示一个单一问题的代价，子问题对应某次递归函数调用。我们将树中每层中的代价求和，得到每层代价，然后将所有层的代价求和，得到所有层次的递归调用总代价。简单来说就是将递归的一层一层分析出来，再累加求和。

递归树最适合用来生成好的猜测，然后可用代入法来验证猜测是否正确。当使用递归树来生成好的猜测时，常常要忍受一点儿“不精确”，因为关注的是如何寻找解的一个上界。

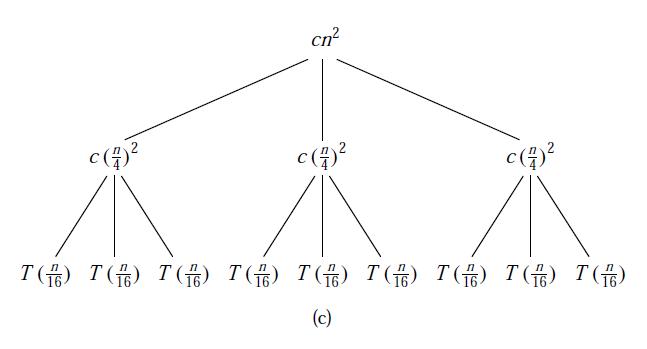
示例

在递归树中，每一个结点都代表一个子代价，每层的代价是该层所有子代价的总和，总问题的代价就是所有层的代价总和。所以，我们利用递归树求解代价，只要知道每一层的代价和层数即可。

这些，都需要直观的找出规律，以上图为例，当递归调用到叶子T(1)时所用到的递归次数就是整棵递归树的深度。我们从图中可以得到第i层的结点的代价为n/(4^i)，当n/(4^i)=1即i = log4(n)时，递归到达了叶子，故整棵递归树的深度为log4(n)。总代价是所有层代价的总和。

主方法（最普适）

定理4.1（主定理） 令 a≥1 和 b>1 是常数，f(n) 是一个函数，T(n) 是定义在非负整数上的递归式：
$T(n) = aT(n/b) + f(n)$
那么T(n)有如下渐进界：

  1. 若对某个常数 ε>0 有 f(n) = O(nlogb^a^-ε)，则 T(n) = Θ(nlogb^a^) 。
  2. 若 f(n) = Θ(nlogba)，则 T(n) = Θ(nlogb^a^lgn) 。
  3. 若对某个常数 ε>0 有 f(n) = Ω(nlogb^a^+ε)，且**对某个常数 c<1 和所有足够大的 n 有 af(n/b) ≤ cf(n)**，则 T(n) = Θ(f(n)) 。

将余项f(n)与函数 nlogb^a^ 进行比较， 直觉上来说两个函数的较大者决定了递归式的解，如情况一是 nlogba 较大，情况3是 f(n) 较大。而情况2是两者一样大，这种情况需要乘上一个对数因子。

这里要注意主方法不能求解的地方，所有的大于和小于都是多项式意义上的大于和小于，对于有些递归式夹在三种情况的间隙中，是无法用主方法来求解的。下面解释一下什么是多项式意义上的小于和大于：

f(x)多项式大于g(x):存在实数e>0,使得f(x)>g(x)n^e^
f(x)多项式小于g(x):存在实数e>0,使得f(x)<g(x)n^e^

举个例子，有递归式T(n) = 2T(n/2)+nlgn。

对于这个递归式，我们有 a = 2，b = 2， f(n) = n，因此 nlogb^a^ = nlog2^2^ = Θ(n^1^) 。

但是nlogn仅仅渐进大于n

因为对于任意c>0,均有logn < n^c^(由洛必达法则可知)。

示例

T(n) = 9T(n/3) + n

对于这个递归式，我们有 a = 9，b = 3， f(n) = n，因此 nlogb^a^ = nlog3^9^ = Θ(n^2^) 。而 f(n) = n 渐进小于 Θ(n^2^)，所以可以应用于主定理的情况1，从而得到解 T(n) = Θ(n^2^) 。

T(n) = T(2n/3) + 1

其中，a = 1， b = 3/2， f(n) = 1，因此 nlogb^a^ = nlog3/2^1^ = n^0^ = 1 。由于 f(n) = Θ(1) ，与Θ(nlogb^a^)恰好相等，可应用于情况2，从而得到解 T(n) = Θ(lgn) 。

T(n) = 3T(n/4) + nlgn

我们有 a = 3，b = 4，f(n) = nlgn，因此nlogb^a^ = nlog4^3^ = O(n^0.793^) 。由于 f(n) = Θ(nlgn) = Ω(n) = Ω(n^0.793+0.207^)，因此可以考虑应用于情况3，其中 ε = 0.207。但需要检查是否满足条件：当 n 足够大时，存在 c<1 使 af(n/b) ≤ cf(n) 。

  • 令 3f(n/4) ≤ cf(n) 有
    3n/4lg(n/4) ≤ cnlgn
    3/4(lgn - lg4) ≤ clgn
    (3/4 - c)lgn ≤ 3/4lg4

容易发现，当 c ≥ 3/4 时，上式对于足够大的 n 恒成立。因此可以使用主定理的情况3，得出递归式的解为 T(n) = Θ(nlgn) 。

最大子数组问题

已知数组A，在A中寻找“和最大”的非空连续子数组。——称这样的连续子数组为最大子数组(maximum subarray)

方法一：暴力求解

暴力求解的时间复杂度为O（n^2^）

方法二：分治求解

分治求解的核心在于递归。所以需要考虑最大子数组如何满足递归的要求。

首先，将数组分成均分为两个部分。那么最大子数组可能存在的位置可能存在的情况有三种：

  1. 最大子数组在左边的数组中
  2. 最大子数组在右边数组中
  3. 最大子数组跨越了左右两个子数组

递归的结束：左右子数组的元素为1时，就可以结束递归了。

递归层需要做的事情：计算左右子数组的最大子数组和横跨左右子数组的最大数组。
在求解横跨左右子数组的最大数组时，可以从mid出发，分别向左和向右找出“和最大”的子区间，mid分别是左右区间的终点和起点。然后合并这两个区间即可得到跨越中点时的A[low … high]的最大子数组。

递归的返回值：返回MAX（左右子数组的最大子数组，横跨左右子数组的最大数组）

性能分析

对A[low..mid]和A[mid+1..high]两个子问题递归求解，每个子问题的规模是n/2，所以每个子问题的求解时间为T(n/2)，两个子问题递归求解的总时间是2T(n/2)。

FIND-MAX-CROSSING-SUBARRAY的时间是Θ(n)。

所以T(n)=Θ(nlgn）

示例

Leetcode 53.最大子序和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public int maxSubArray(int[] nums) {
        int l = nums.length;
        if(l==0)
        return 0;
        return maxSubArraySum(nums,0,l-1);
    }
    public int maxSubArraySum(int[] nums,int l,int r)
    {
        
        //递归的结束：当只有子数组只有一个元素的时候
        if(l==r)
        return nums[l];
        int mid=(r+l)/2;
        int temp  = Math.max(maxSubArraySum(nums,mid+1,r),maxCrossingSum(nums,l,mid,r));
        return Math.max(maxSubArraySum(nums,l,mid),temp);
    }
    public int maxCrossingSum(int[] nums,int l,int mid ,int r)
    {
        int sum=0;
        int leftsum=Integer.MIN_VALUE;
        //从mid的左边走，一直走到最大子数组的位置
        for(int i=mid;i>=l;i--)
        {
            sum+=nums[i];
            if(sum>=leftsum)
            leftsum=sum;
        }
        sum=0;
        int rightsum=Integer.MIN_VALUE;
        for(int i=mid+1;i<=r;i++)
        {
            sum+=nums[i];
            if(sum>rightsum)
            rightsum=sum;
        }
        return leftsum+rightsum;
    }
}

Strassen矩阵乘法

矩阵乘法是种极其耗时的运算。

以C = A • B为例，其中A和B都是 n x n 的矩阵。根据矩阵乘法的定义，计算过程如下：

1
2
3
4
5
6
7
8
9
SQUARE-MATRIX-MULTIPLY(A, B)
n = A.rows
let C be a new nxn matrix
for i = 1 to n
    for j = 1 to n
        c[i][j] = 0
        for k = 1 to n
            c[i][j] += a[i][k] * b[k][j]
return C

由于存在三层循环，它的时间复杂度将达到O(n3)。

这是一个很可怕的数字。但是，凭着科学家们的智慧，这个数正在一步步下降。本文介绍经典的Strassen算法，该算法将时间复杂度降低到O(nlg7) ≈ O(n2.81)。别小看这个细微的改进，当n非常大时，该算法将比平凡算法节约大量时间。

分治法

Strassen算法基于分治的思想，因此我们首先考虑一个简单的分治策略。

每个 n x n 的矩阵都可以分割为四个 n/2 x n/2 的矩阵：

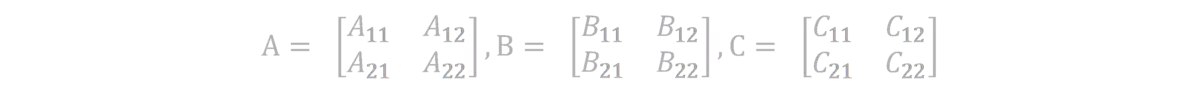
因此可以将公式C = A • B改写为

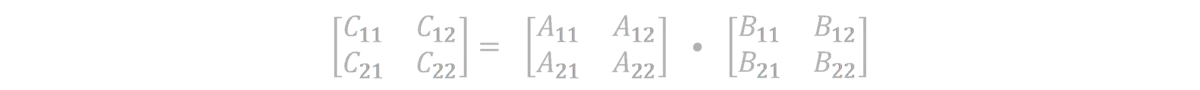
于是上式就等价于如下四个公式：

（式3-3）
C11 = A11 • B11 + A12 • B21
C12 = A11 • B12 + A12 • B22
C21 = A21 • B11 + A22 • B21
C22 = A21 • B12 + A22 • B22

注：任意两个子矩阵块的乘可以沿用同样的规则：如果子矩阵的阶大于2，则将子矩阵分成更小的子矩阵，直到每个子矩阵只含一个元素为止。从而构造出一个递归计算过程。

每个公式需要计算两次矩阵乘法和一次矩阵加法，使用T(n)表示 n x n 矩阵乘法的时间复杂度，那么我们可以根据上面的分解得到一个递推公式。

T(n) = 8T(n/2) + Θ(n^2^)

其中，8T(n/2)表示8次矩阵乘法，而且相乘的矩阵规模降到了n/2。Θ(n^2^)表示4次矩阵加法的时间复杂度以及合并C矩阵的时间复杂度。

要想计算出T(n)并不复杂，可以采用画递归树的方式计算，结果是T(n) = Θ(n^3^)

可见，简单的分治策略并没有起到加速运算的效果。

Strassen算法

让我们回头观察前面使用分治策略的时候为什么无法提高速度。

因为分解后的问题包含了8次矩阵相乘和4次矩阵相加，就是这8次矩阵相乘导致了速度不能提升。于是我们想到能不能减少矩阵相乘的次数，取而代之的是矩阵相加的次数增加。Strassen正是利用了这一点。

现在，我们来看一下Strassen算法的原理。

仍然把每个矩阵分割为4份，然后创建如下10个中间矩阵：

S1 = B12 - B22
S2 = A11 + A12
S3 = A21 + A22
S4 = B21 - B11
S5 = A11 + A22
S6 = B11 + B22
S7 = A12 - A22
S8 = B21 + B22
S9 = A11 - A21
S10 = B11 + B12

接着，计算7次矩阵乘法：

P1 = A11 • S1
P2 = S2 • B22
P3 = S3 • B11
P4 = A22 • S4
P5 = S5 • S6
P6 = S7 • S8
P7 = S9 • S10

最后，根据这7个结果就可以计算出C矩阵：
C11 = P5 + P4 - P2 + P6
C12 = P1 + P2
C21 = P3 + P4
C22 = P5 + P1 - P3 - P7

我们可以把P矩阵和S矩阵展开，并带入最后的式子计算，会发现恰好是公式3中的四个式子。也就是说，Strassen为了计算公式3，绕了一大圈，用了更多的步骤，成功的把计算量变成了7个矩阵乘法和18个矩阵加法。虽然矩阵加法增加了好几倍，而矩阵乘法只减小了1个，但在数量级面前，18个加法仍然渐进快于1个乘法。这就是该算法的精妙之处。

同样地，我们可以写出Strassen算法的递推公式：

T(n) = 7T(n/2) + Θ(n2)

使用递归树或主方法可以计算出结果：

T(n) = Θ(nlg7) ≈ Θ(n2.81)

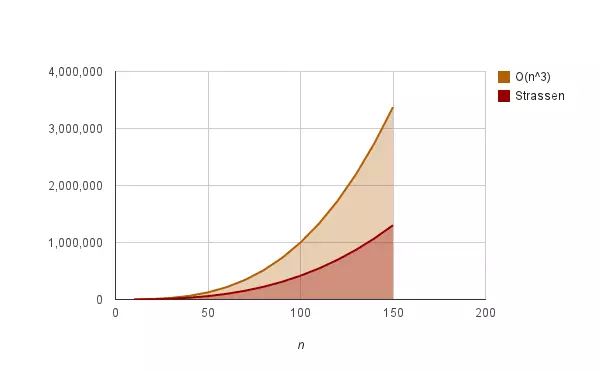
下图展示了平凡算法和Strassen算法的性能差异，n越大，Strassen算法节约的时间越多。

性能比较

最近点对问题

发表于 更新于 分类于 ，

CPU的组成和功能

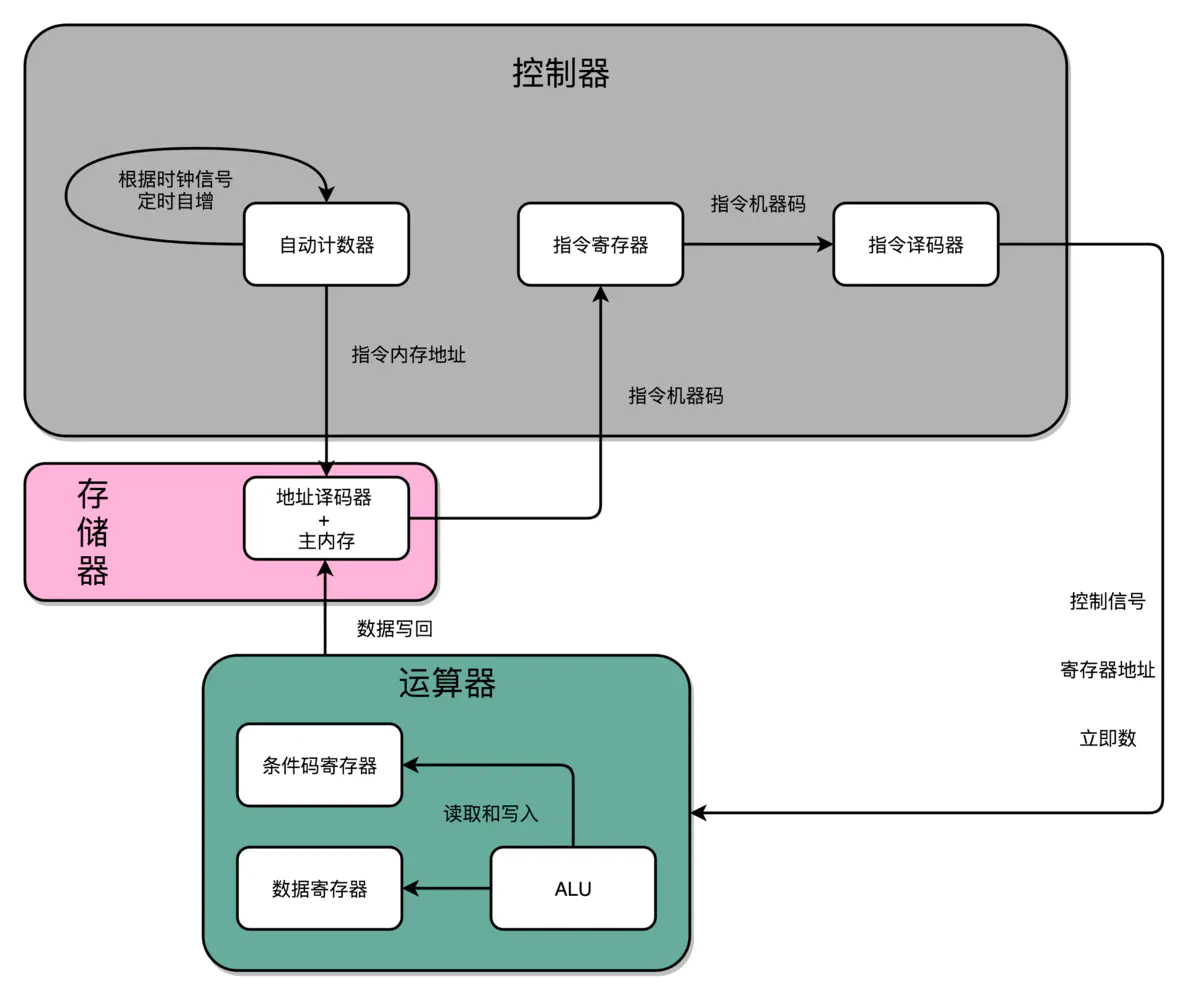
cpu=运算器+控制器。

运算器：数据加工。

控制器：

  • 程序控制: 程序中指令执行顺序控制
  • 操作控制: 将机器指令翻译成执行部件所需操作控制信号
  • 时序控制: 控制操作信号的产生时间、持续时间
  • 异常控制: 异常处理，外设交互

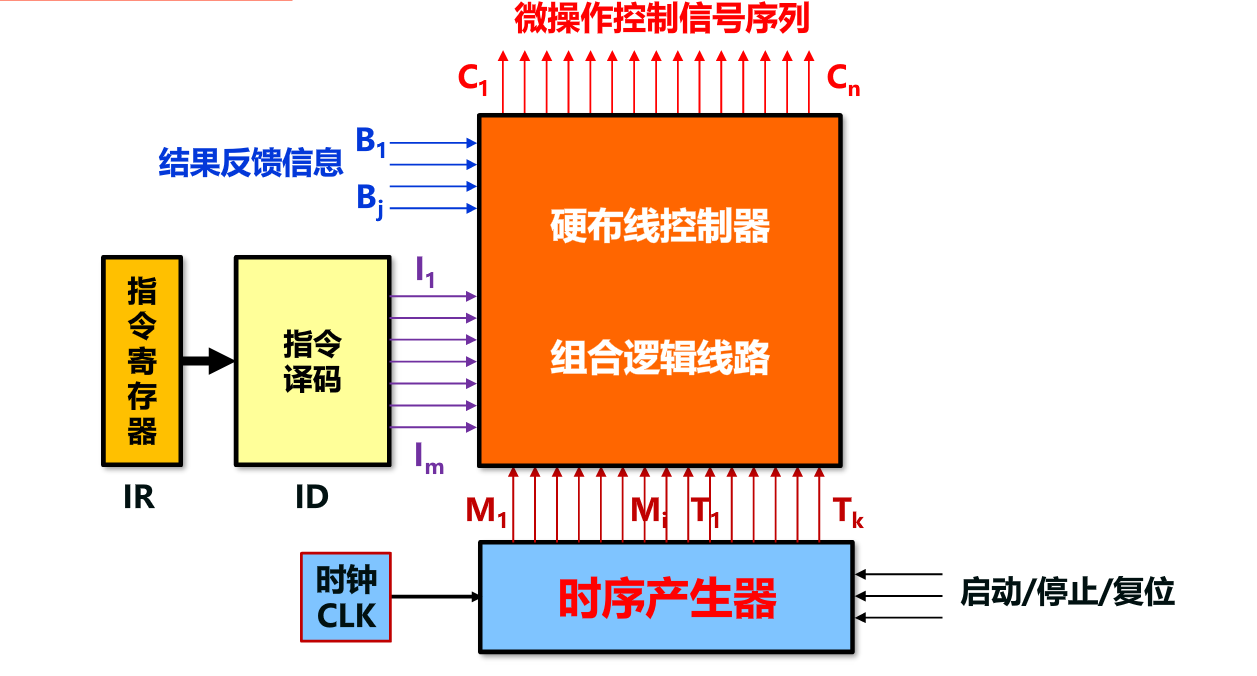
控制器

控制器：程序计数器、指令寄存器、指令译码器、时序产生器和操作控制器组成。

取指令，将机器指令译码并生成执行部件所需的控制信号序列，控制信号送至各执行部件控点，引起逻辑门开闭，建立正确的数据通路，从而完成指令功能。

  • 硬布线控制器 (时序逻辑型) (硬件实现)
  • 微程序控制器 (存储程序型) (软件实现)

指令周期

在指令的执行周期完成后，处理器会判断是否出现中断请求，只有在出现中断请求时才会进入中断周期。

数据通路

执行部件间传送信息的路径（数据流）

  • 共享通路（总线）
  • 专用通路

在总线结构中，可同时进行的数据传输数量取决于总线的数量

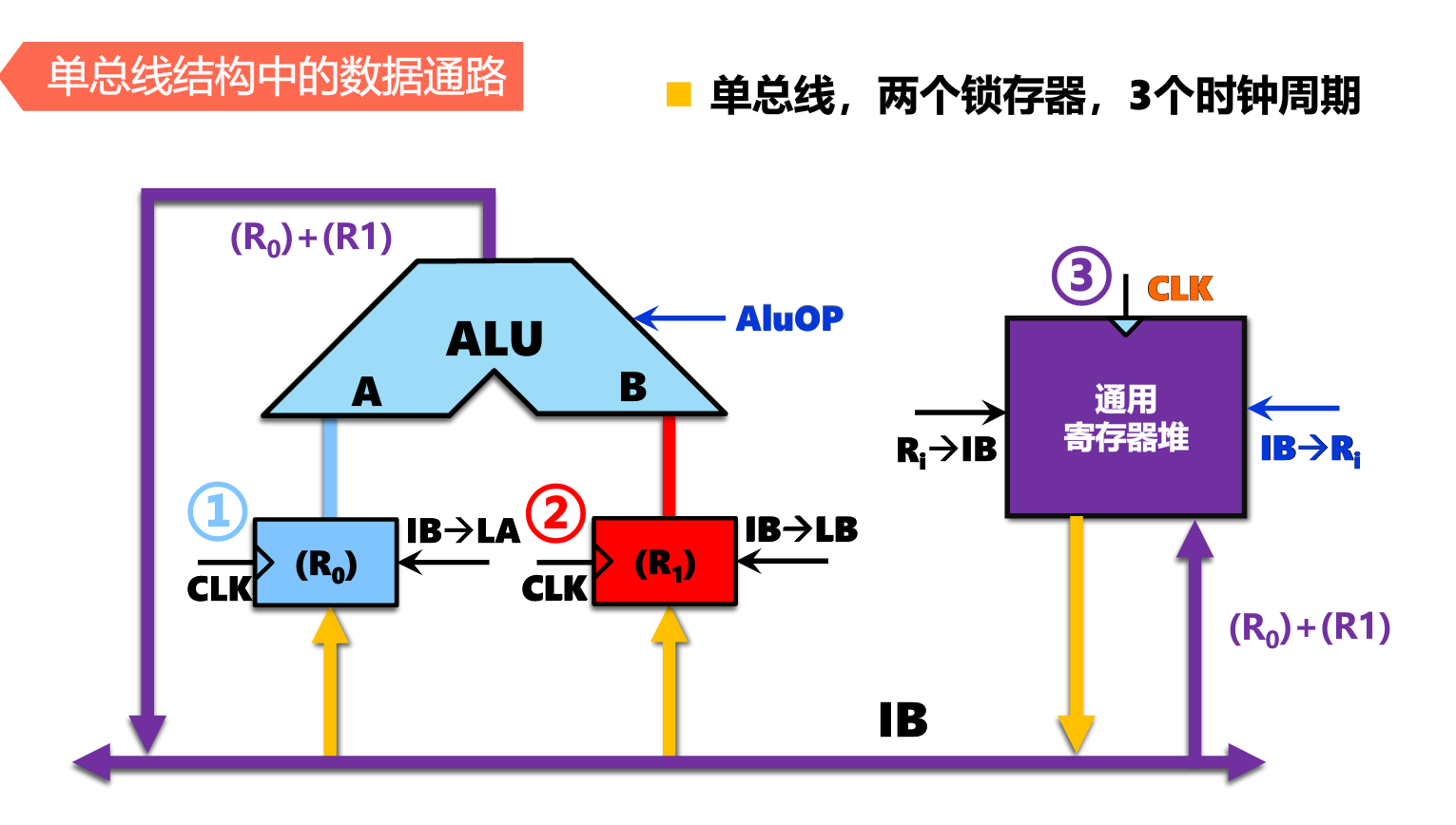
单总线结构

总线上可以有多个模块同时接收数据，但是某一时刻只能有一个模块向总线发送数据。因此，接入到总线上的部件需要进行输出控制，以防止总线上的数据冲突。

双总线结构

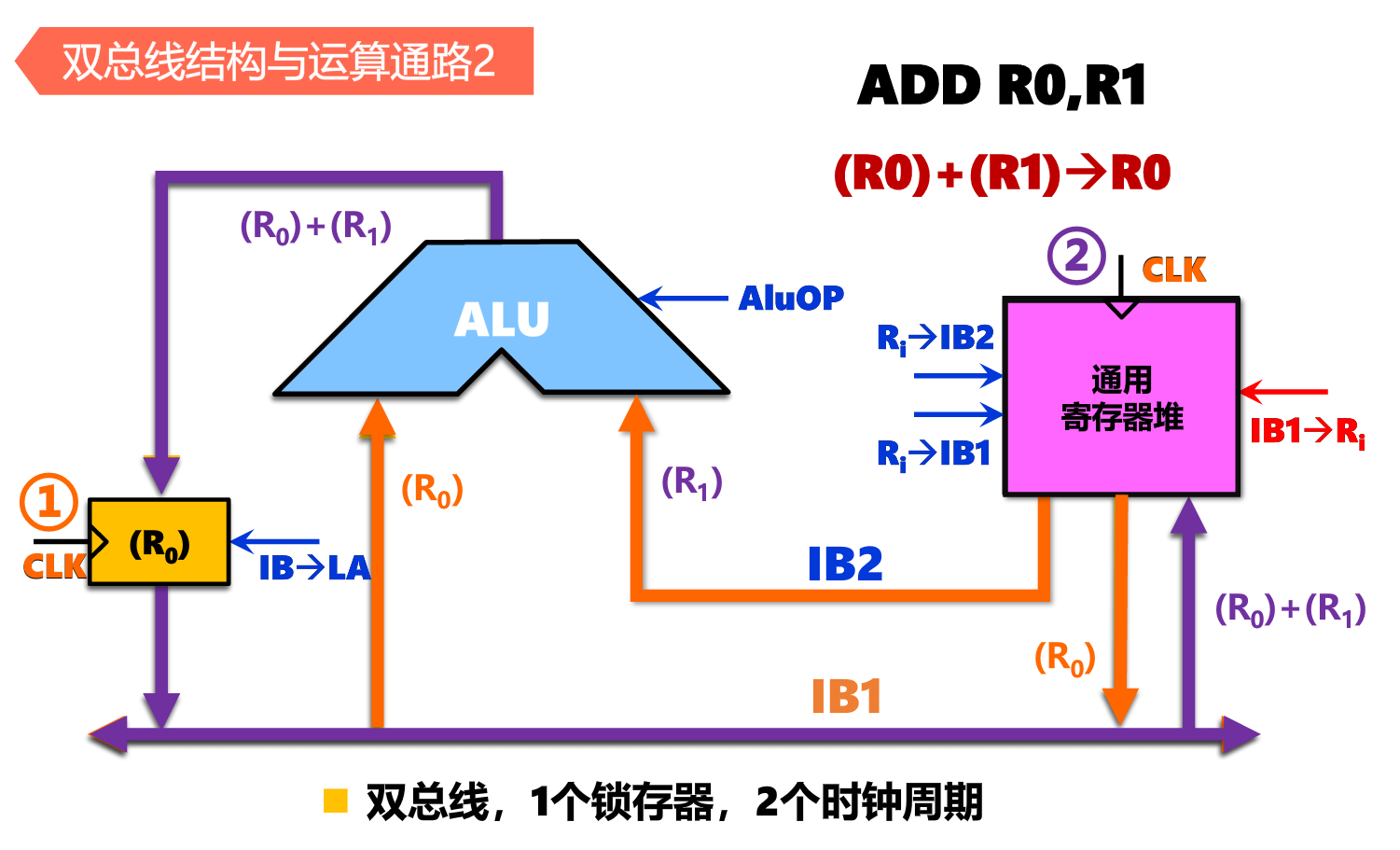
三总线结构

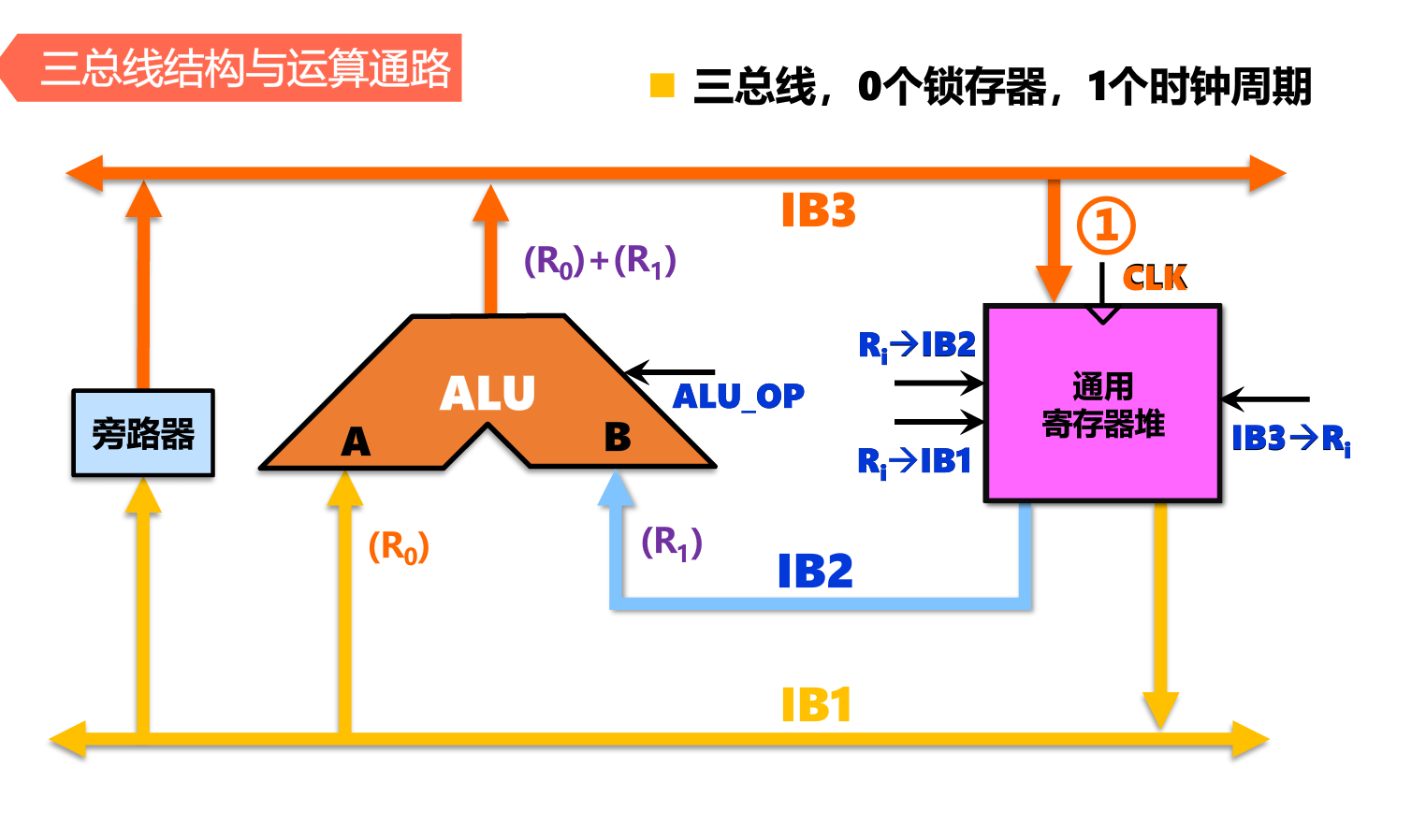
指令周期与时序（重要）

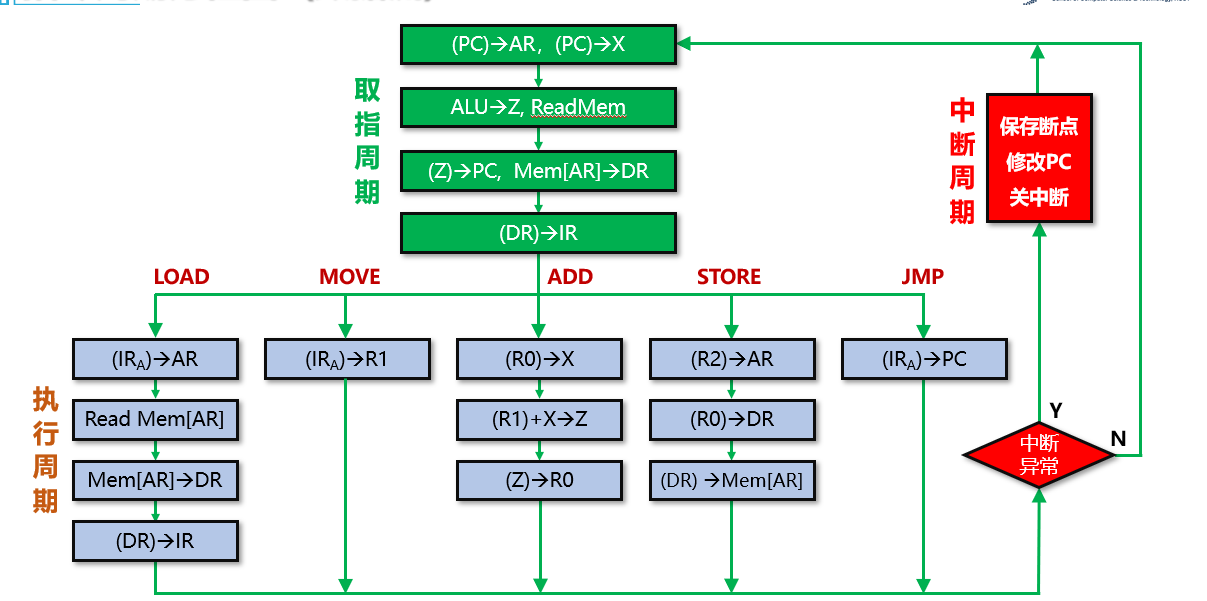
指令周期

  • 定长指令周期：传统的三级时序—–以最慢的指令周期同步
  • 变长指令周期：指令需要多少时间就给多少时间

取指令、执行指令反复循环

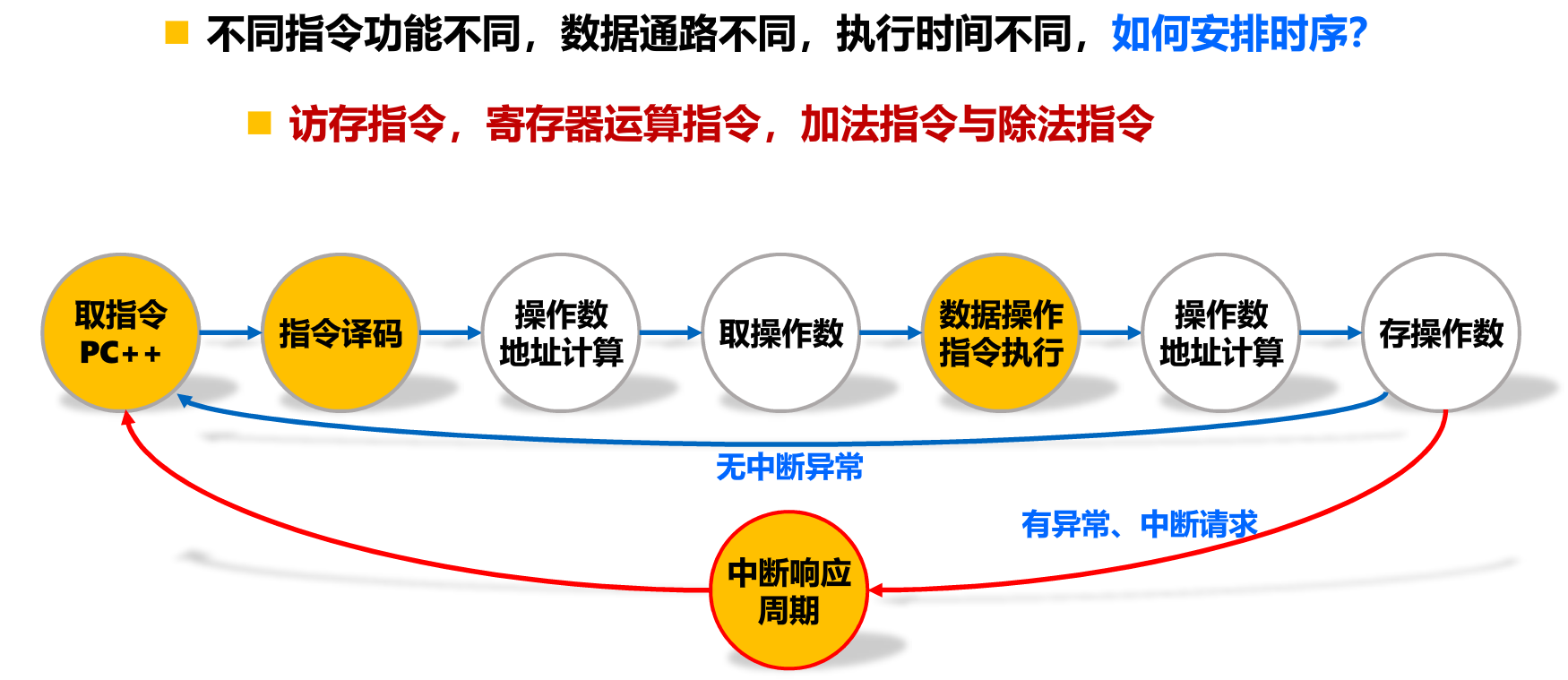
  • 时钟周期（震荡周期、节拍脉冲） ——能完成依次微操作
  • 机器周期（CPU周期）= 多个时钟周期 ——–从主存读出一条指令的最短时间（也就是访问一次内存的最短时间）

指令周期可划分如下阶段

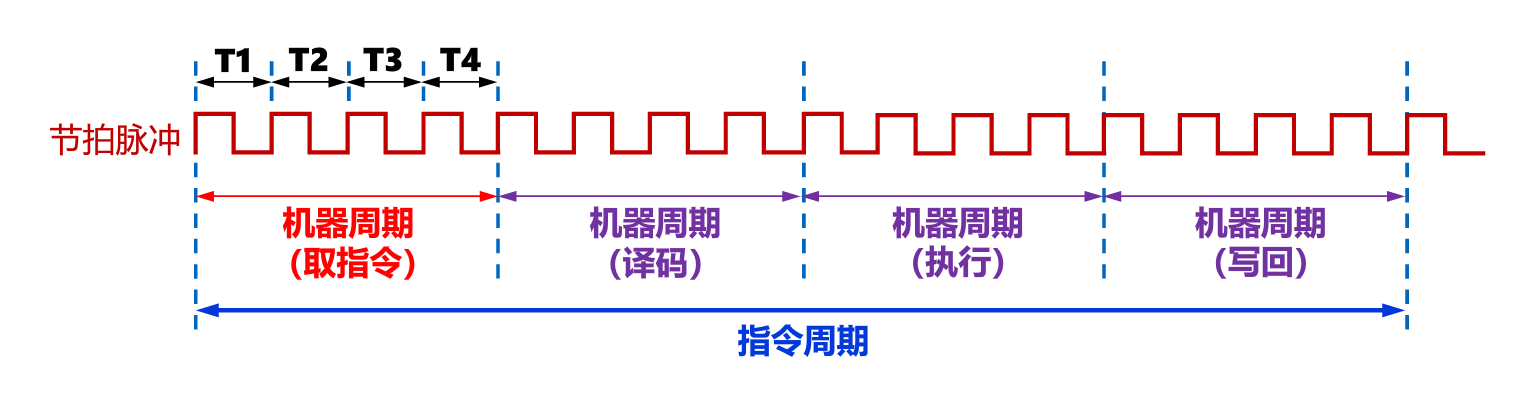
取值周期

取值周期就是按PC内容取出指令，并计算后续指令的地址：
有跳转指令的就计算跳转后的指令的地址；没有就顺序执行。

译码/取操作数周期

识别指令类型，并根据指令地址码字段的值访问相应的寄存器或主存单元。

这部分包括了操作数地址计算和取操作数的阶段。

执行周期

控制器向算术逻辑运算单元和数据通路中的其他部件发送操作控制命令，对前面准备好的操作数进行操作，将操作的状态信息保存在PSW中。如果出现程序转移，则在执行周期内决定转移地址

写回

将运算结果写到寄存器或存储器中。

PS

实际的指令周期还包括了中断周期（完成现行程序与中断程序的切换）、总线周期（完成总线操作与总线控制权的转移）、IO周期（完成输入输出操作）。

指令周期数据流示例

可以分析分析与不同总线的数据通路之间的运行的周期数。

时序

硬布线控制中采用的时序体制是三级时序体制。微程序控制器采用的是两级时序体制。

时序产生器与控制器–同步控制

时序产生器循环产生周期电位、节拍电位，供控制器对信号进行时间调制。简单来说就是对各种信号进行时间同步。

现代时序系统—异步控制

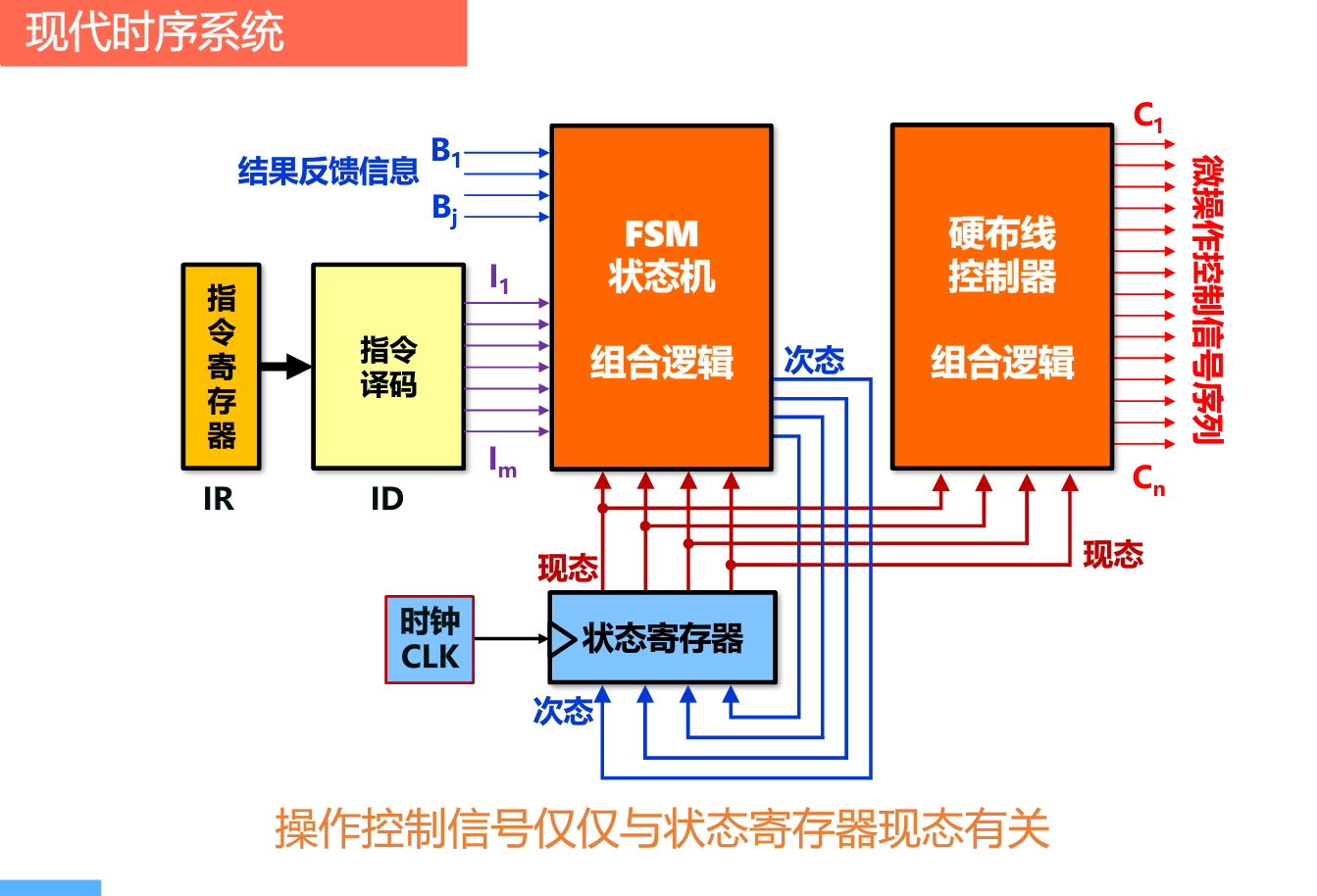
控制方式

  • 同步控制方式—–使用的是定长指令周期
  • 异步控制方式—–使用的是变长指令周期
  • 混合控制方式—–使计算机处于同步和异步交替工作方式

硬布线控制器

基本原理

将控制器看成产生固定时序控制信号的逻辑电路。

单周期硬布线控制器

使用的是同步控制

固定指令周期硬布线控制器设计步骤

1、设计三级时序产生器：所有指令固定机器周期数、节拍数
2、列出所有机器指令的指令周期流程图，明确每个节拍的控制信号
3、找出产生同一微操作控制信号的条件
4、写出各微操作控制信号的布尔表达式
5、化简
6、实现

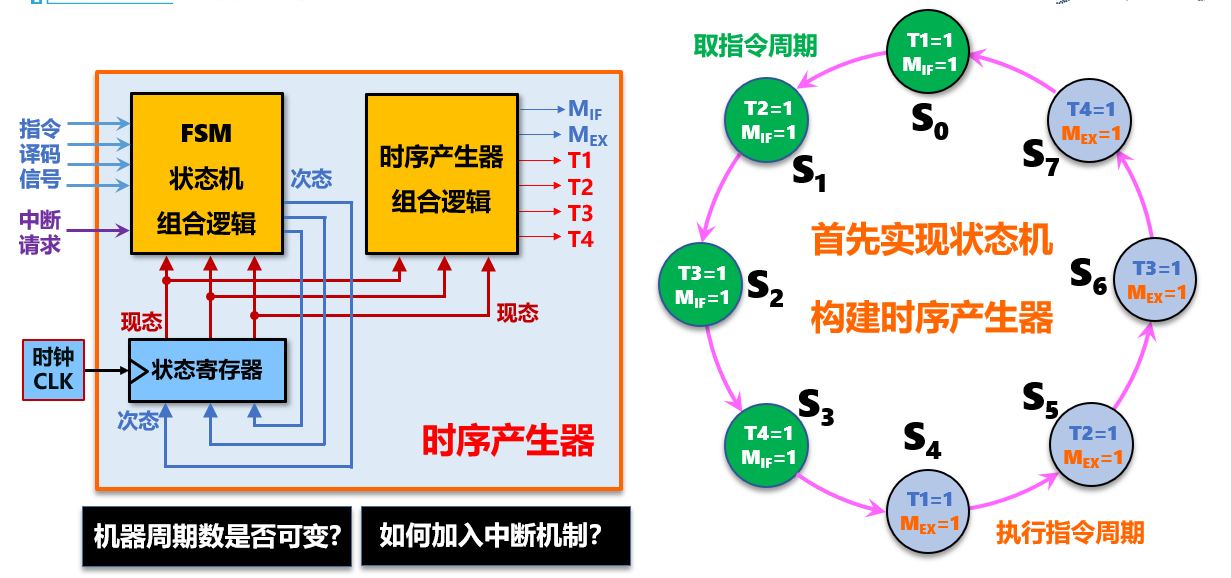
多周期硬布线控制器

核心是设计时序产生器状态机

使用的是异步控制

  • 一条指令多个时钟周期
  • 一个时钟周期一个状态
  • 一个状态对应一组并发信号

可变周期硬布线控制器设计步骤

1、列出所有机器指令的指令周期流程图，明确每个节拍的控制信号
2、绘制指令执行状态转换图
3、根据状态转换图构建状态机真值表，实现有限状态机组合逻辑
4、实现控制器组合逻辑电路

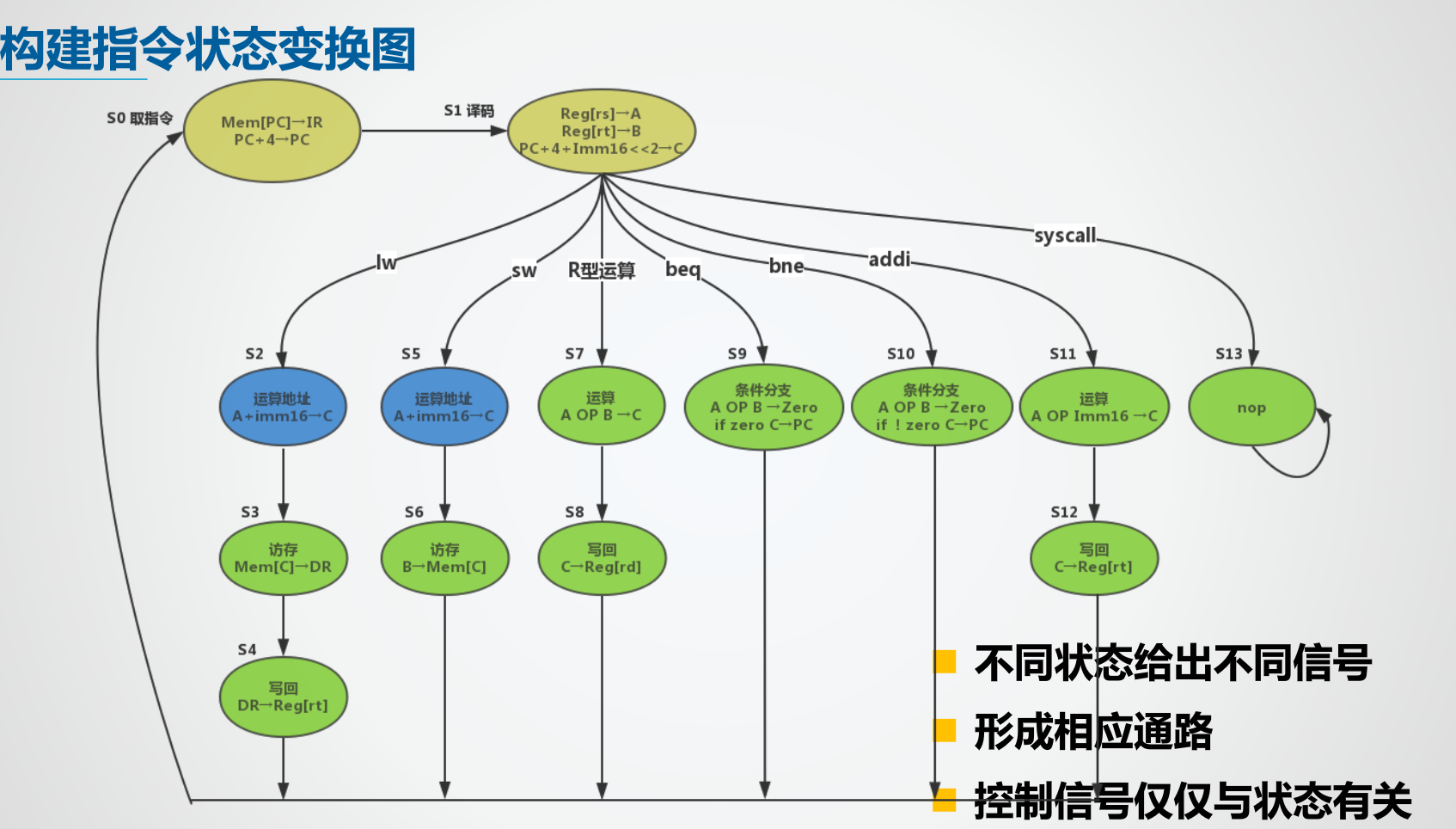
指令结束阶段可能会进入中断

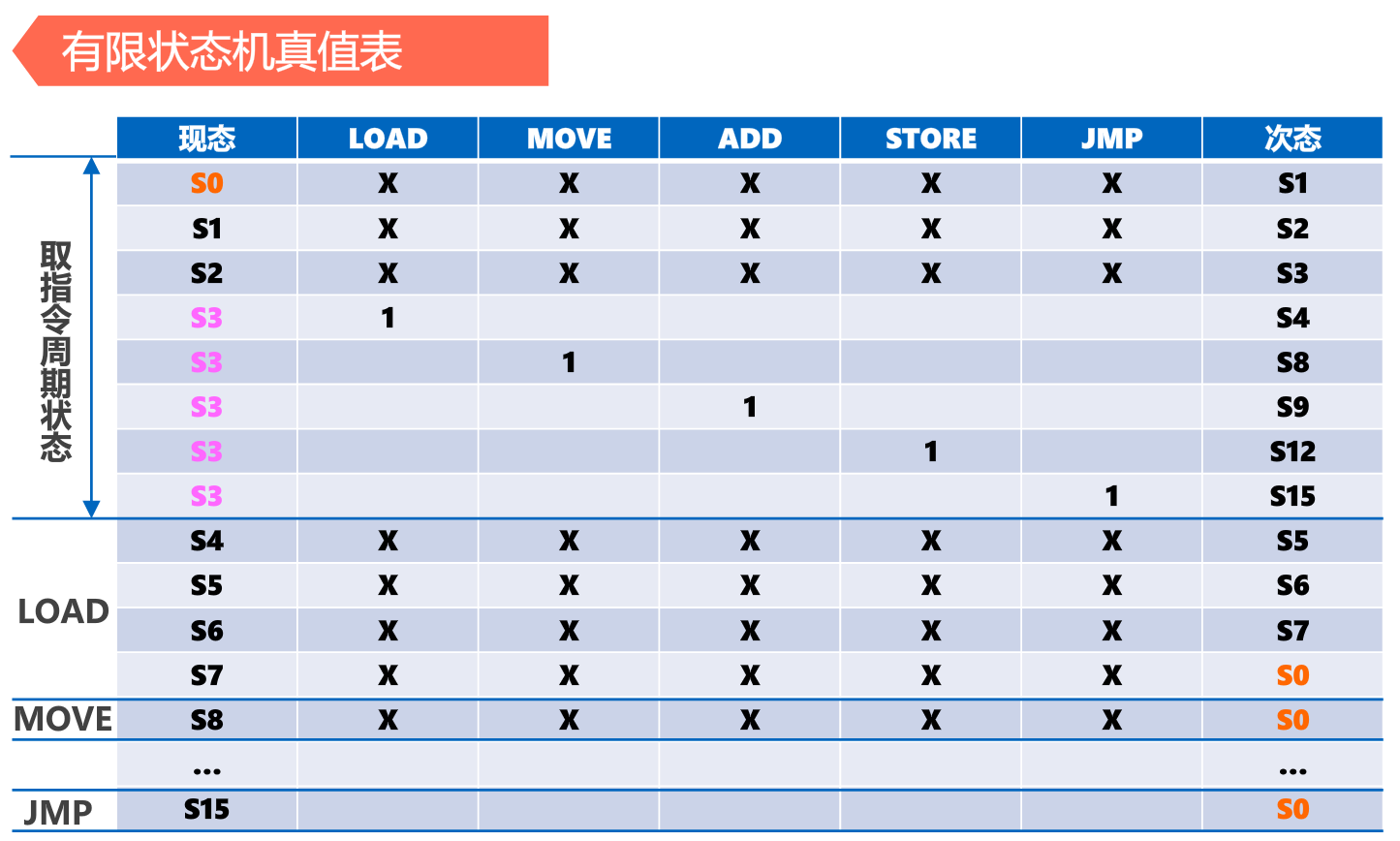
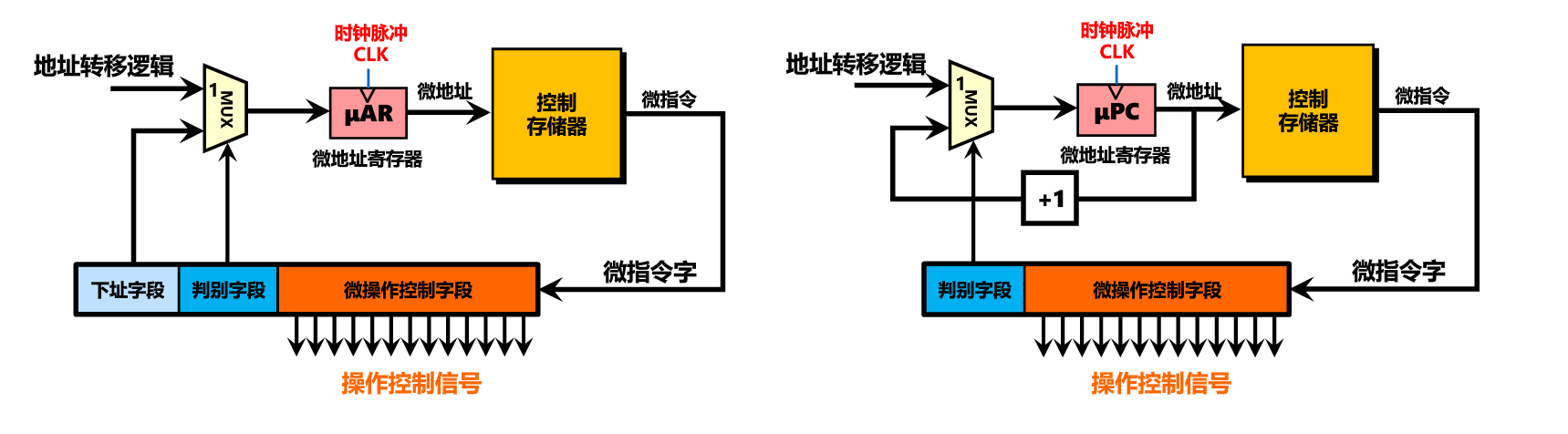
微程序控制器

使用的是 存储逻辑

  • 将并发信号事先存储为微指令
  • 一条指令对应多条微指令
  • 状态等同与存储器地址

微程序控制器是利用软件方法来设计硬件的技术。将完成指令所需要的控制信号按格式编写成微指令，存放到控制存储器。

  • 一条机器指令对应一段微程序（多条微指令）
  • 指令取指执行—>微程序的执行—–>执行多条微指令—–>依次生成控制信号

微命令和微操作

微程序–>微指令–>微命令

微命令：控制部件向执行部件发出的各种控制命令

微操作：执行部件收到微命令后所进行的操作

微命令是可以在CPU周期内并行执行的，但是微程序是只能串行执行。

操作控制字段是微指令主体，每一位都是一个微指令。

微程序中多条微指令的先后关系由微指令格式中的测试字段和下地址字段给出。

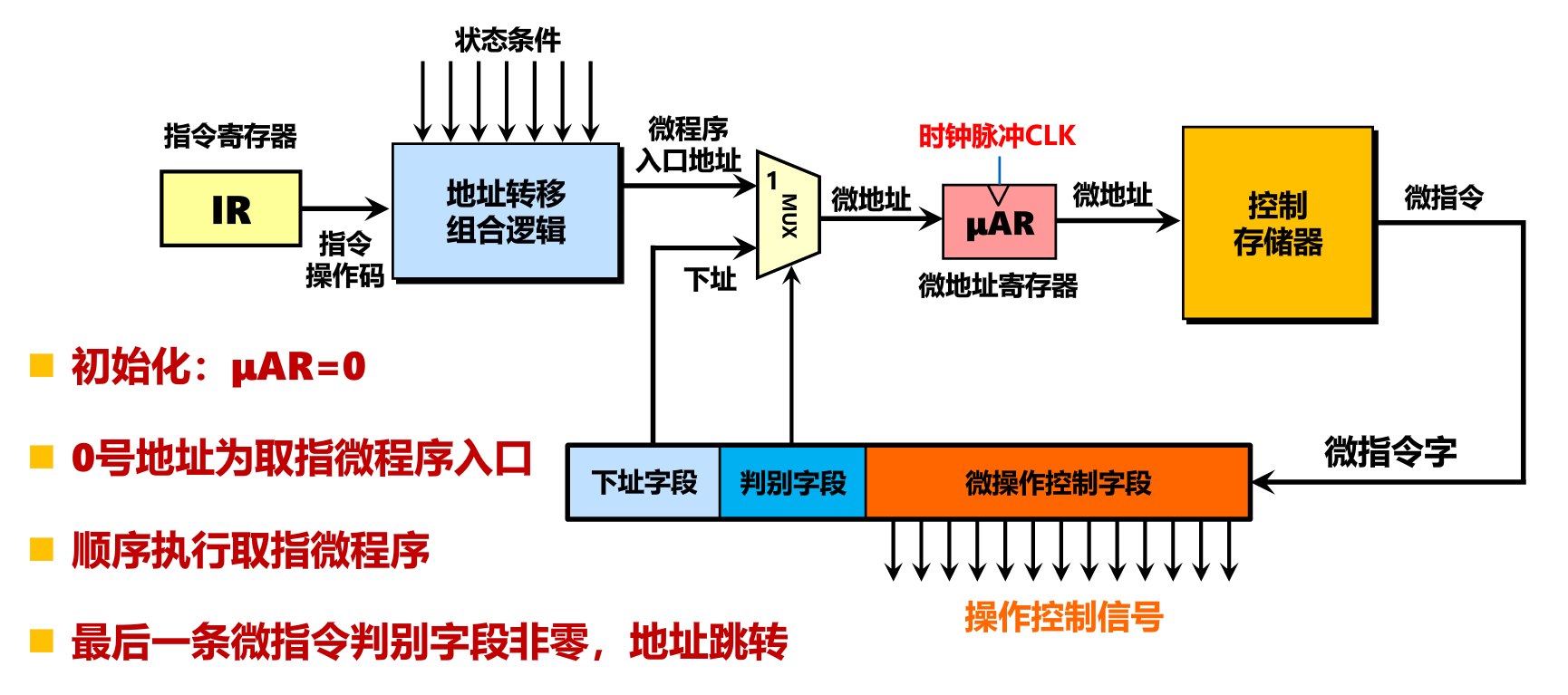
微程序设计

微指令格式

分为水平型和垂直型。

水平型微指令

在一个微周期中同时给出多个微命令的微指令。编码方式如下“微指令编码方式”

垂直型微指令

类似汇编语言，把微指令代码化。

基本上淘汰了。

微指令编码方式

直接表示法

将微指令操作控制字段的每一个二进制位定义成一个微命令，用1或者0表示相应的微命令的有无。

缺点：字长太长

解决方法：

  • 改直接表示为编码表示
  • 去掉下址字段，采用PC=PC+1的方式生成微指令
  • 改水平微指令为垂直微指令（牺牲并行性）

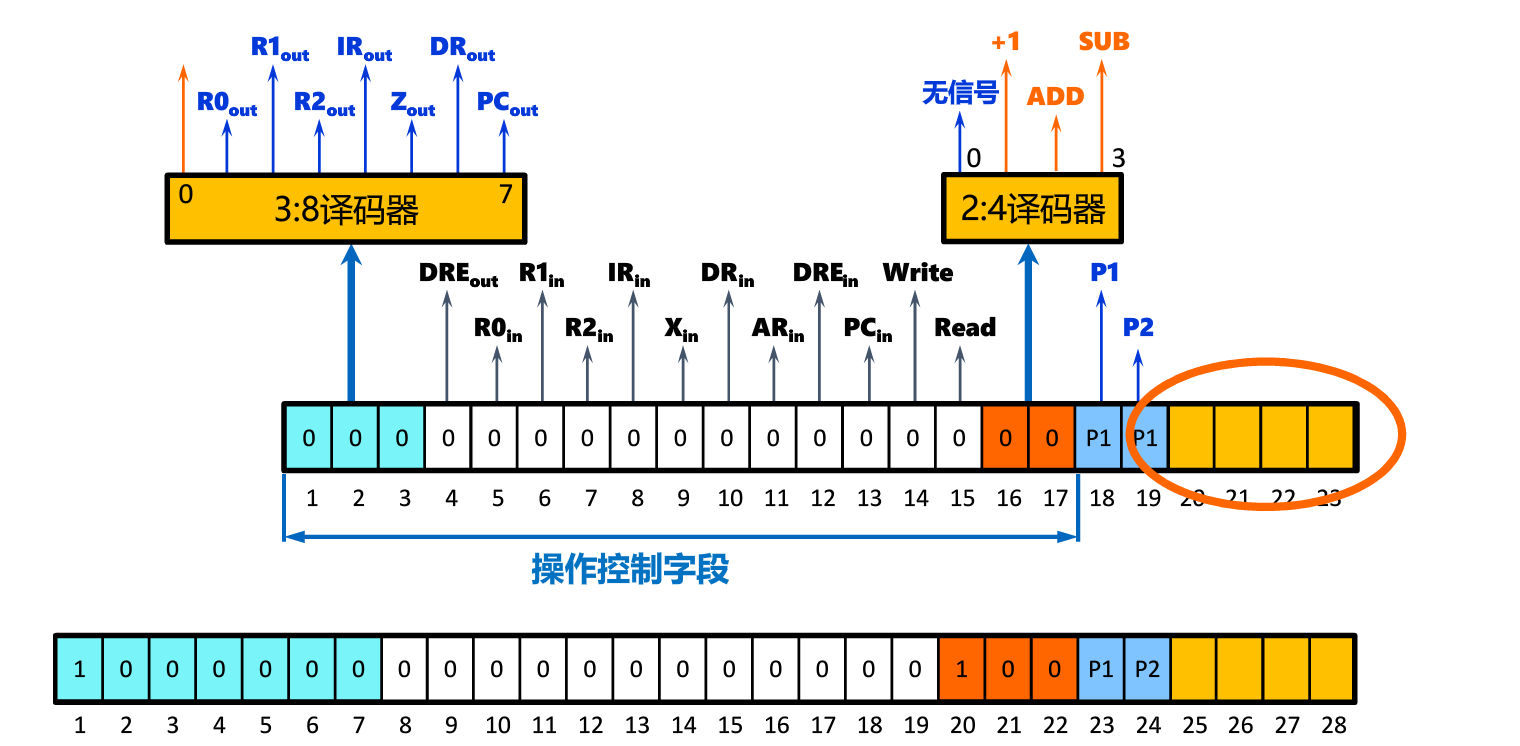
此时没有下址字段，故PC的生成方式如下图所示：

字段直接译码法

将微指令格式中的操作控制字段分成诺干组，每组中包含诺干个互斥性微命令，将相容性微命令安排在不同组。（将互斥性微命令编码是因为他们之间是不可能同时出现的）

注意：要预留一个信号表示什么指令都不给

PS

一些名词的含义

指令周期：取指令并执行一条指令所需要的时间，一般由若干个机器周期组成，包括从取指令、分析指令到执行完所需的全部时间。

数据通路：数据在功能部件之间传送的路径。

时钟周期：由CPU时钟定义的定长时间间隔，是CPU工作的最小时间单位，也称节拍脉冲或T周期。

同步控制：选取部件中最长的操作时间作为统一的时间间隔标准，使所有部件都在这个时间间隔内启动并完成操作。

异步控制：系统不设立统一的时间间隔标准(基准时钟除外)，各部件按各自的时钟工作，分别实现各自的时序控制，时间衔接通过应答通讯方式(又称握手方式)实现。

联合控制：同步控制与异步控制相结合。对大多数节拍数相近的指令，采用同步控制；而对少数节拍数多不固定的指令，采用异步控制。

单周期处理器：所有指令在一个时钟周期内完成的处理器。

多周期处理器：每条指令的执行分成多个阶段，每个时钟周期完成一个阶段的工作。

微操作：执行部件收到微命令后所进行的操作。

相容性微命令：能同时并行执行的微命令。

互斥性微命令：不能并行执行的微操作。

微指令：由微指令产生的一组实现一定微操作功能的微命令的组合。

微程序：实现一条指令功能的若干条微指令的集合。

微程序控制器：采用微程序设计方法设计的控制器。指令执行过程中所需要的所有控制信号以微指令的方式存在在控制存储器中，指令执行时，逐条读出微指令，以产生执行执行过程中所需要的控制信号。

控制存储器：微程序控制器中用于存放解释所有指令微程序的存储器。

硬布线控制器：又称为组合逻辑控制器，指令执行所需要的控制信号直接由逻辑门电路和触发器等构成的电路产生，与微程序控制器相比，具有结构复杂但速度快的特点。

一些问题

1)中央处理器的基本功能是什么?从实现其功能的角度分析，它应由哪些部件组成?

答：五方面的功能：

指令执行顺序的控制。即控制程序中的指令按事先规定的顺序自动地执行，从而保证程序执行过程中，指令在逻辑上的相互关系不被改变。

指令的操作控制。即产生指令执行过程中所需要的信号，以控制执行部件按指令规定的操作运行。

时间控制，即对每个控制信号进行定时，以便按规定的时间顺序启动各操作。对于任何一条指令而言，如果操作控制信号的时间不正确，则指令的功能也就不能正确实现。

数据加工处理。即对数据进行算术、逻辑运算，或将数据在相关部件之间传送。

异常和中断处理。如处理运算中的异常及处理外部设备的中断服务请求等。

组成：中央处理器主要由控制器和运算器两部分构成。控制器的主要功能包括：取指令、计算下一条指令的地址、对指令译码、产生相应的操作控制信号、控制指令执行的步骤和数据流动的方向。运算器是执行部件，由算术逻辑单元和各种寄存器组成。

2)CPU内部有哪些寄存器?它们的功能分别是什么?

答：**(1)** **指令寄存器(IR)**：IR用于保存指令。从主存储器取出的指令存放在IR中，直到新的指令从主存中取出为止。

(2) 程序计数器(PC) ：PC保存将要执行的指令地址，故又称指令地址寄存器。CPU取指令时，将PC的内容送到主存地址寄存器，然后修改PC的值形成下一条将要执行的指令地址

(3) **地址寄存器(AR)**：AR用来保存当前CPU所要访问的主存单元地址，无论CPU是取指令还是存取数据，都必须先将要访问的主存单元地址送AR，直到读/写操作完成。

(4)**通用寄存器组(GR)**：通用的含义是指寄存器的功能有多种用途，GR可作为ALU的累加器、变址寄存器、地址指针、指令计数器、数据缓冲器，用于存放操作数(包括源操作数、目的操作数及中间结果)和各种地址信息等。

(5) 数据缓冲寄存器(DR)

DR作为CPU和主存之间的数据缓冲寄存器用于存放操作数、运算结果或中间结果，以减少访问主存的次数；也可存放从主存中读出的数据，或准备写入主存的数据。

(6) 程序状态字寄存器(PSW)

PSW用于保存由算术运算指令、逻辑运算指令、测试结果等建立的各种条件标志。常见的状态信息包括进位标志(C)、溢出标志(V)、结果为负数标志(S)及结果为零标志(Z)等。

**3)**什么是取指周期?取指周期内应完成哪些操作?

答：取指周期就是从开始取指令到取指令完成所需要的时间。取指周期要完成两方面的操作，一是将PC的值送存储器地址寄存器MAR，并完成储单元去取指令；二是如何形成后续指令地址：

·顺序执行指令时，将PC内容加当前指令所占用的主存单元数(以字节为单位)；

·当出现转移时，根据寻址方式、转移条件、转移的目标地址等内容计算得到。

**4)**指令有几种执行方式?说明各自的特点。

答：指令的执行方式有顺序执行方式、重叠执行方式和流水执行三种方式。

顺序执行方式：是一种串行执行方式，取出一条指令的操作全部结束后才能开始下一条指令的指令周期，这种方式控制简单，程序的执行速度慢。

重叠执行方式：是一种局部并行方式，通常将当前指令的执行阶段与下一条指令的取指阶段重叠进行，这种方式控制较复杂，但可以提高程序的执行速度；

流水执行方式：是一种并行执行方式，它将指令的执行分多个阶段（每个阶段的任务由特定的功能部件完成），一般而言，在该执行方式下，指令间的并行程度比重叠执行方式要高，控制更为复杂，可以更快地提高程序的执行速度。

**5)**计算机为什么要设置时序系统?说明指令周期、机器周期、和时钟周期的含义。

答：指令执行过程中的所有操作必须按照一定的次序完成，而且这些操作持续的时间也有严格的限制，因此，在计算机系统中需要设置时序系统，对指令执行过程中的所有控制信号进行时间控制，以保证指令功能的正确实现。

通常将一条指令从取出到执行完成所需要的时间称为指令周期，包括取指周期和执行周期，指令周期通过右若干和机器周期组成，所包含的机器周期的数量随指令功能和寻址方式的不同而不同。

机器周期分成若干个节拍电位时间段，通常以CPU完成一次微操作所需要的时间为基础来定义节拍电位的时间；由CPU时钟定义的定长时间间隔，是CPU工作的最小时间单位，也称节拍脉冲或T周期。

  1. 组合逻辑控制器与微程序控制器各有什么特点?

答：硬布线控制器又称为组合逻辑控制器，这种控制器中的控制信号直接由各种类型的逻辑门电路和触发器等构成，与微程序控制器相比，具有结构复杂但速度快的特点。

微程序控制器的设计采用了存储技术和程序设计技术，使复杂的控制逻辑得到简化。通过过读出存放在微程序控制器中微指令产生指令执行过程中所需要的控制信号，所以，与硬布线控制器相比，微程序控制器的速度较慢。

  1. 说明程序与微程序，指令与微指令的异同

答：微程序是多条微指令系列的集合,用于实现指令的功能,属于机器指令级别，对用于的透明性不强，存放在CPU内的控制存储器中；程序则是为了完成某一应用功能所编写的指令（包括机器语言指令或高级语言指令）集合，属于高级语言级别，对用户的透明性好，运行时存放在计算机的主存中。

指令是指挥计算机执行某种功能的命令，是构成程序的基本单位，由操作码和地址字段构成；而微指令则用于微程序控制器中产生指令执行过程中所需要的微命令，是构成微程序的基本单位，由操作控制字段、判别测试字段和下地址字段等组成。

**8)**微命令有哪几种编码方法?它们是如何实现的?

答：微指令的微命令有三种编码方法，分别是直接表示方法、字段直接译码法和混合控制法。

直接表示法的基本思想是：将微指令操作控制字段的每个二进制位定义为一个微命令，用“1”或“0”表示相应的微命令的“有”或“无”。

字段直接译码法的基本思想是：将微指令格式中的操作控制字段分成若干组，每组中包含若干个互斥性微命令，将相容性的微命令安排在不同组。

混合控制法：将直接表示法与字段直接译码法混合使用，以便在微指令字长、并行性及执行速度和灵活性等方面进行折衷，发挥它们的共同优点。

9)简述微程序控制器和硬布线控制器的设计方法?

答： 微程序控制器设计方法：

1)分析指令执行的数据通路，列出每条指令在所有寻址方式下的执行操作流程和每一步所需要的控制信号；

2)对指令的操作流程进行细化，将每条指令的每个微操作分配到具体的机器周期的各个时间节拍信号上；

(3)设计微指令格式、微命令编码方法和程序组织方式；

(4)编制每条指令的微程序；并按照所设计的微程序组织方式存放到控存中；

(5)对微命令进行同步控制，并送数据通路的相关控制点。

硬布线控制器设计方法：

1)分析指令执行的数据通路，列出每条指令在所有寻址方式下的执行操作流程和每一步所需要的控制信号；

2)对指令的操作流程进行细化，将每条指令的每个微操作分配到具体的机器周期的各个时间节拍信号上，即对操作控制信号进行同步控制。

3)对每一个控制信号进行逻辑综合，得到每个控制信号的逻辑表达式。

4)最后采用逻辑门或PLA或ROM实现逻辑表达式的功能，各控制信号送数据通路的相关控制点。

发表于 更新于 分类于 ，

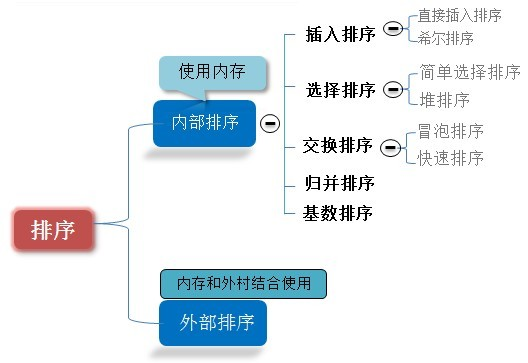
概叙

术语说明：

  • 稳定 ：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
  • 不稳定 ：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；
  • 内排序 ：所有排序操作都在内存中完成；
  • 外排序 ：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；

当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序。

快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；

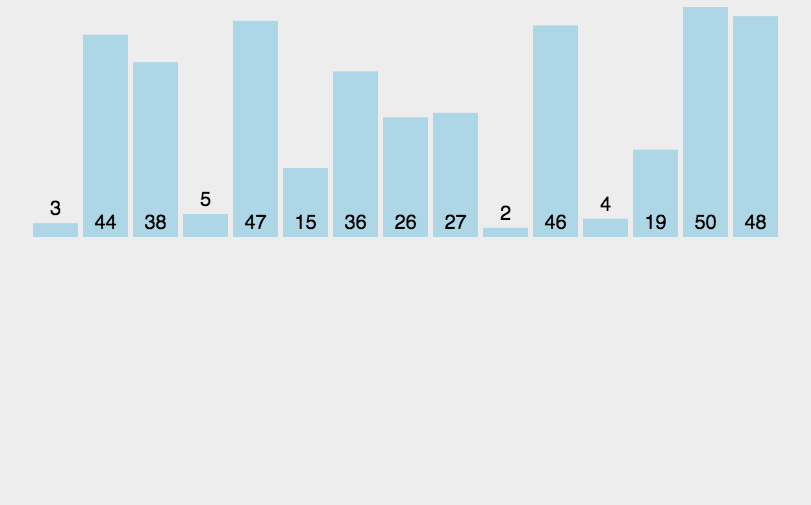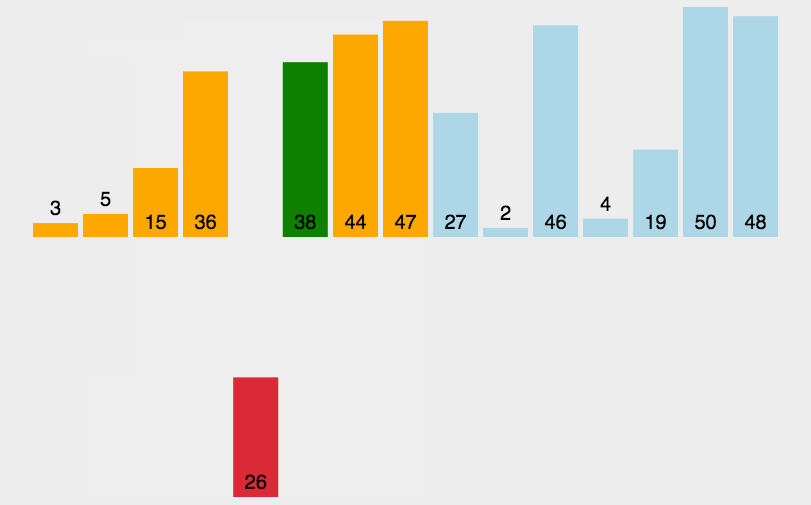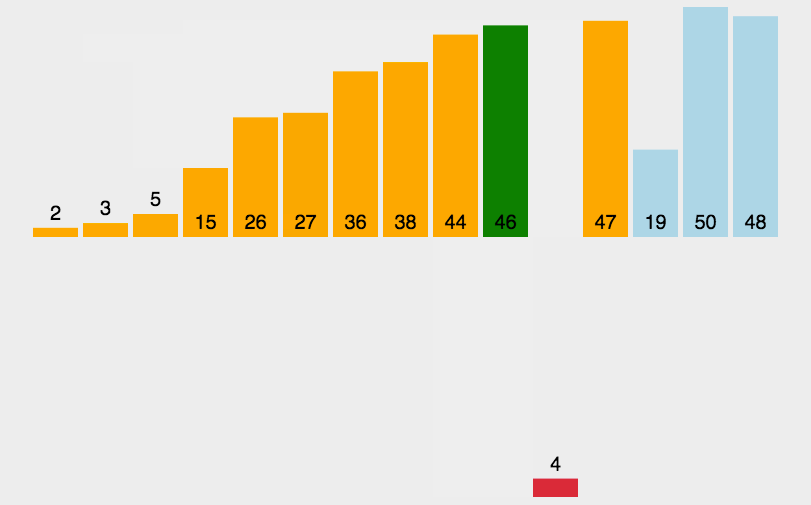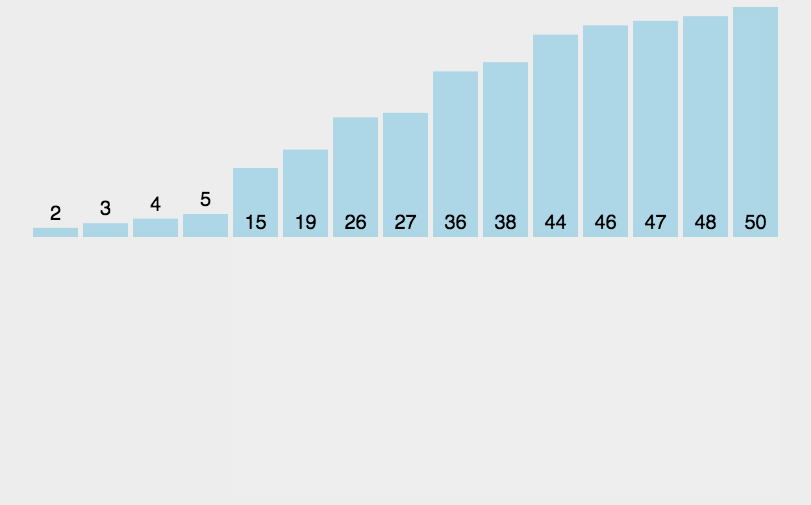
1.插入排序—直接插入排序(Straight Insertion Sort)

插入排序简单来说就是不断从后面将数据插入前面已经排好序的过程。

由此可知：前面的队列一定是排好序的。在插入的过程中可能会导致前面排好序的数据往后移，腾出位置。

动画演示：

2.归并排序（Merge Sort）

简单来说，归并排序就是将一个无序的序列分解成诺干个有序的子序列，然后依次归并。

一般采取的是递归的方式进行设计。

递归的结束标志是：当分解的序列只有一个元素时。

递归层需要做的是：将子序列排序。

递归层返回的是：排好序的子序列

递归请见：

动画演示：

看不明白？再看一个。

3、堆排序（Heap Sort）

堆排序（Heapsort） 是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

  • 算法描述
  • 步骤1：将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；
  • 步骤2：将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
  • 步骤3：由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。
  • 演示

算法分析

  • 最佳情况：T(n) = O(nlogn)
  • 最差情况：T(n) = O(nlogn)
  • 平均情况：T(n) = O(nlogn)

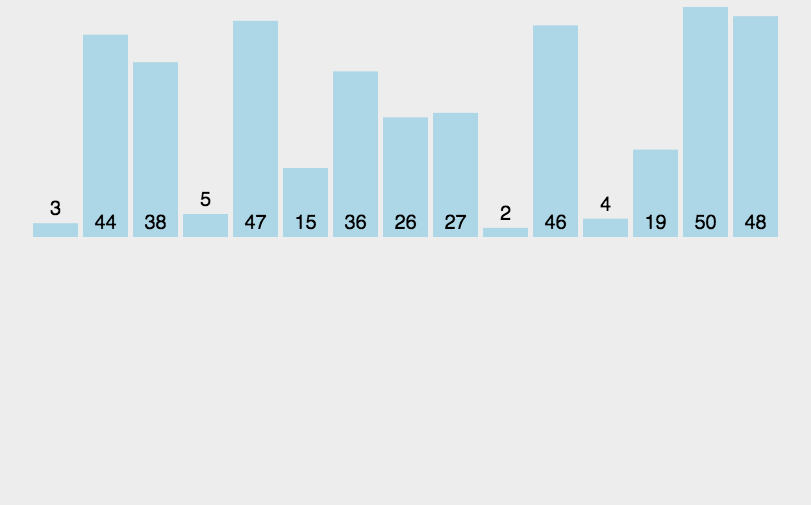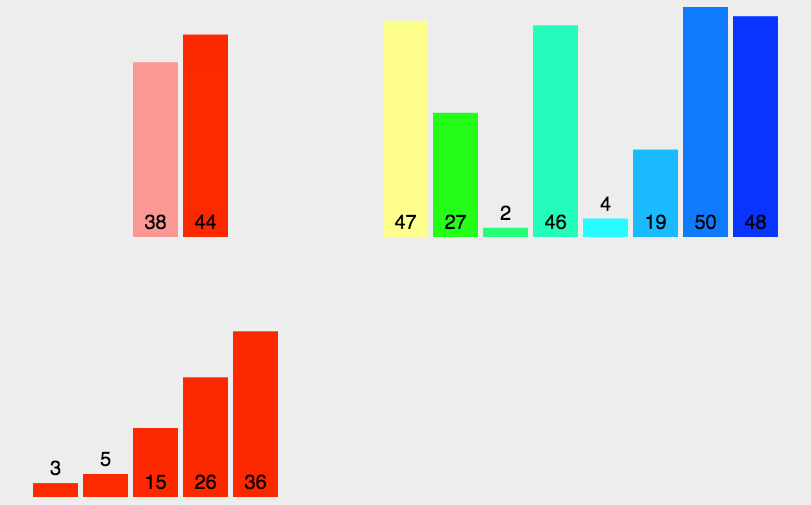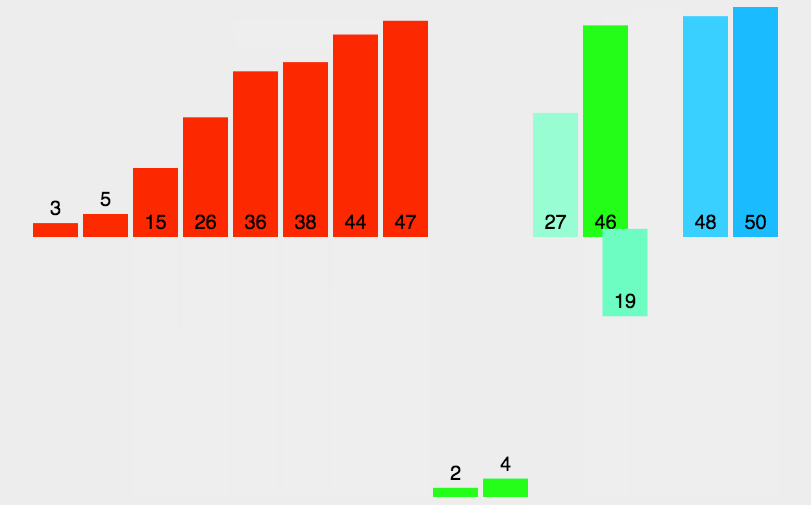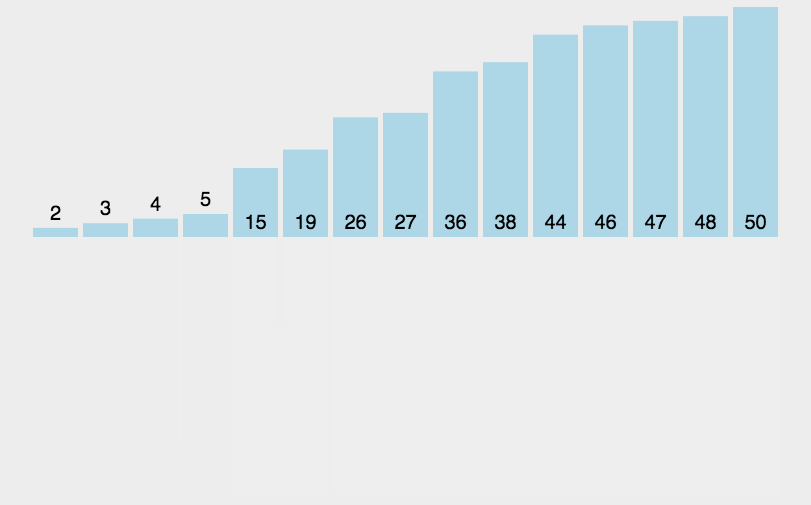
4、快速排序（Quick Sort）

快速排序 的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

  • 算法描述

    快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

    • 步骤1：从数列中挑出一个元素，称为 “基准”（pivot ）；
    • 步骤2：重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
    • 步骤3：递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

  • 示例

概括来说为 挖坑填数+分治法

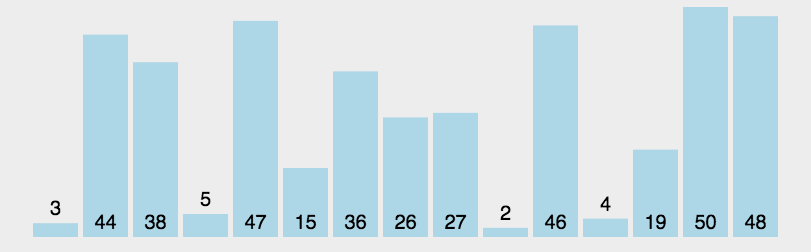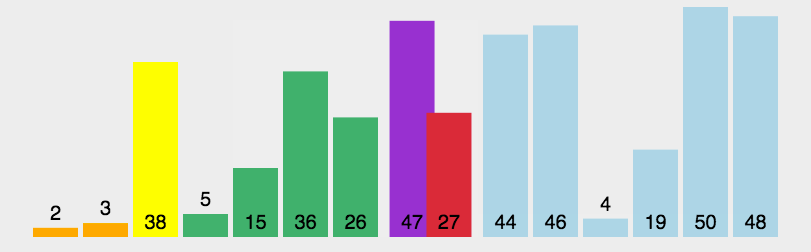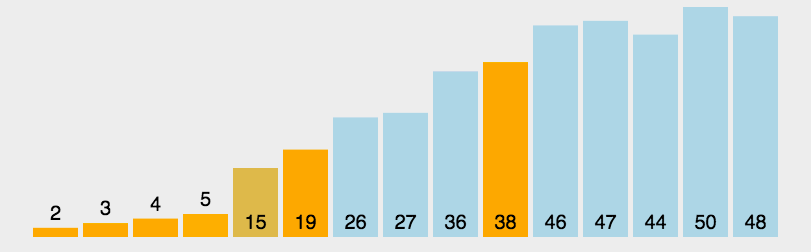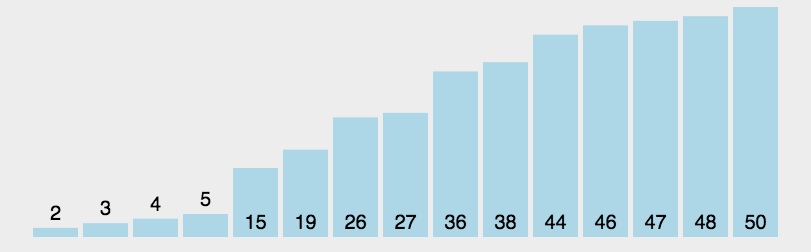
下面举例来进行说明，主要有三个参数，i为区间的开始地址，j为区间的结束地址，X为当前的开始的值

第一步，i=0,j=9,X=72（X可以理解成此时a[0]是挖了一个洞，东西放在X哪里。这个洞可以填入其他数据）

0 1 2 3 4 5 6 7 8 9
72 6 57 88 60 42 83 73 48 85

第二步，从j开始由后向前找，找到比X小的第一个数a[8]=48,此时：a[0]=a[8]；i++
进行替换。这样a[0]这个坑被填上了，但是a[7]这个坑多出来了。

0 1 2 3 4 5 6 7 8 9
48 6 57 88 60 42 83 73 72 85

第三步，从i开始由前往后找，找到比X大的第一个数a[3]=88,（此处找比X大的数是因为在后半截的数据均要比72才算实现目的）此时：a[8]=a[3]；j–
a[8]的坑被填上了，但是a[3]的坑又出现了。

0 1 2 3 4 5 6 7 8 9
48 6 57 88 60 42 83 73 88 85

此时：i=3；j=7；X=72（因为经过上几轮的比较，我们可以得出前3个数均比72小，后3个数都比72大，不予考虑）

再重复上面的步骤，先从后向前找，再从前向后找。

第四步，从j=7开始由后向前找，找到比X小的第一个数a[5]=42，a[3] = a[5]; i++;

0 1 2 3 4 5 6 7 8 9
48 6 57 42 60 42 83 73 88 85

第五步，从i=5开始由前往后找，i=j=5，所以退出，将X填入a[5]

0 1 2 3 4 5 6 7 8 9
48 6 57 42 60 72 83 73 88 85

一轮结束。

接下来对两个子区间[0,4]和[6,9]重复上面的操作即可

总结：

1．i =L; j = R; 将基准数挖出形成第一个坑a[i]。

2．j–由后向前找比它小的数，找到后挖出此数填前一个坑a[i]中。

3．i++由前向后找比它大的数，找到后也挖出此数填到前一个坑a[j]中。

4．再重复执行2，3二步，直到i==j，将基准数填入a[i]中

  • 动图演示

算法分析

  • 最佳情况：T(n) = O(nlogn)
  • 最差情况：T(n) = O(n2)
  • 平均情况：T(n) = O(nlogn)

排序算法的下界

排序，涉及到被排序的序列和排序的方法。（比较）排序算法时间的下界对被排序的序列和排序方法做了以下限制

  • 没有关于被排序序列的先验信息，譬如序列内数据的分布、范围等，即认为序列内元素在一个开区间内均匀分布。同时，序列内元素互异。（可以从两个方面理解元素互异的限制，其一是对于随机的序列而言，两元素相同的概率约为0；其二是比较排序中没有对相同元素的特殊处理）

  • 排序方法中仅仅利用了比较运算来确定元素的顺序。不失一般性，假设每次比较仅取2个元素，比较其大小。

    （比较）排序算法的算法时间复杂度等价为确定输入序列的排列方式需要多少次比较操作。

选择，插入，归并，快速排序算法，在确定排序顺序时都仅仅依赖于对排序关键字对进行比较，它们确定决策时的依据均是”如果这个元素的排序关键字比另一个元素的排序关键字小，那么就进行相应操作，否则，进行其他操作或者什么也不做”，这些排序算法就是比较排序。

基于比较排序的下界

将比较排序定义为仅仅通过比较元素对来确定排序顺序，

Ω符号给出了下界，因此称“对于任意大的n，任何比较排序算法在最坏情况下至少需要cnlgn次比较操作（对于某个常量c成立)”由于每次比较至少需要花费常量时间，对于n个元素的基于比较的排序操作，能够得出一个时间为Ω(nlgn)的下界。

关于此下界的说明：

1.它仅仅指最坏情况。在最坏情况下，该排序必定需要Ω（nlgn)次比较操作。

2.Ω(nlgn)这一下界不依赖于任何算法，只要该算法是一个比较排序。

决策二叉树

决策树：用于证明排序算法的下界，是一个二叉树，每个节点是元素之间一组可能的排序，比较的结果是树的边，下图表示将a，b，c排序的算法

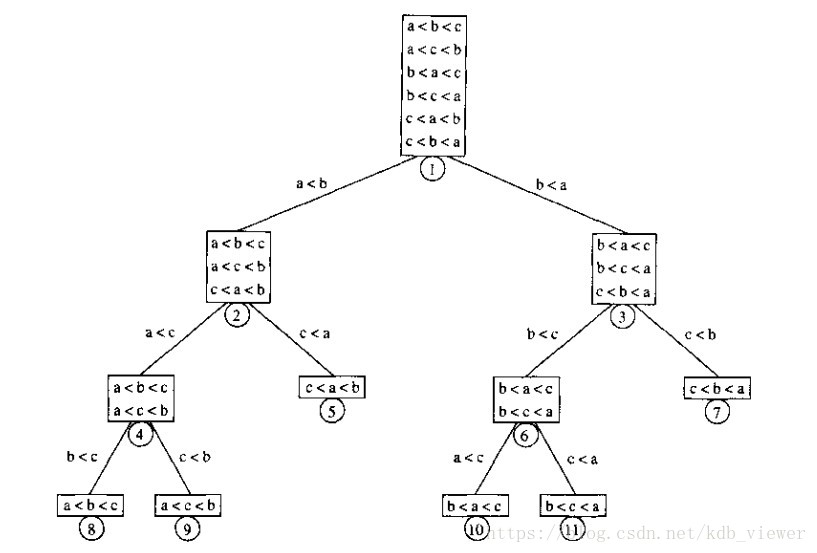
定理：任何只用到比较的算法最坏情况下需要Ω（nlgn)次比较！！

证明：假设高度为h，具有l个可达叶结点的决策树。输入n!种可能的排列都是叶结点，所以n!<=l。且l<=2^h^

两边取对数即可得证。

推论：堆排序和归并排序都是渐近最优的比较排序算法

以比较为基础的有序检索算法最坏情况下的时间下界：

定理 ：设A(1:n)含有n(n≥1)个不同的元素，且有A(1) < A(2) < …< A(n)。

以以比较为基础的算法去判断给定的x是否有，则，最坏情况下，任何这样的算法所需的最小比较次数FIND(n)有：

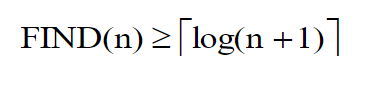
1）任何一种以比较为基础的有序检索算法，在最坏情况下的计算时间都不低于Ο(logn)。因此，不可能存在最坏情况比二分检索数量级还低的算法。

2）二分检索是解决检索问题的最优的最坏情况算法

参考文章：https://blog.csdn.net/MobiusStrip/article/details/83785159

发表于 更新于 分类于 ，

指令系统

  • 指令要求计算机完成什么功能？ - - - -设置操作码
  • 指令要求计算机处理什么数据？ - - - -设置数据源/目
  • 计算机怎样得到要处理的数据？ - - - -设置寻址方式

不同地址数量的指令

分为三地址指令、双地址指令、单地址指令、零地址指令

①三地址指令：一般地址域中A1、A2分别确定第一、第二操作数地址,A3确定结果地址。下一条指令的地址通常由程序计数器按顺序给出。

②二地址指令：地址域中A1确定第一操作数地址和结果地址，A2确定第二操作数地址。

③单地址指令：地址域中A 确定第一操作数地址。固定使用某个寄存器存放第二操作数和操作结果。因而在指令中隐含了它们的地址。

④零地址指令：在堆栈型计算机中，操作数一般存放在下推堆栈顶的两个单元中,结果又放入栈顶,地址均被隐含，因而大多数指令只有操作码而没有地址域。
三地址指令 操作码op address1 address2 address3 （address1） op （address2）-> (address3)
双地址指令 操作码op address1 address2 （address1）op （address2）-> （address1）or（address2）
单地址指令 操作码op address1 （address1）op ->（address1） （address1）op（ACC）-> （address1）

零地址指令：

  1. 机器指令无地址码
  2. 空操作、停机操作、中途返回

寻址方式及指令寻址

顺序寻址

CPU中设置有PC计数器。注意PC+1中的1是一条指令的长度，不是一个字节。

跳跃寻址

就是JMP。

操作数寻址方式

立即数寻址

地址码字段就是操作数本身。

优点：因为将数据和指令一并送入CPU内部的寄存器中，执行指令速度快。便于程序设计。，不需要访问内存

缺点：数据大小受字段位数限制。

MOV AX .2000H

寄存器寻址

操作数已经在CPU的内部寄存器中。

优点：执行速度快。不需要访问内存

缺点：能访问的数据大小一般与计算机字长有关。也受寄存器数量限制

MOV AX ,BX

直接寻址

地址码字段直接给出操作数在内存的地址。

特点：提供了访问主存的操作。

缺点：速度慢。地址字段的位数决定了访问空间大小

MOV AX ,[2000H]

间接寻址

地址码字段给出的是操作数地址的地址。第一次访问主存：获得操作数的地址。第二次访问主存：获得操作数。

明显用速度换访问空间。

MOV AX ,[SOMETHING] //something在内存中。

寄存器间接寻址

地址码字段给出的是寄存器编号。也是两次访问：第一次访问寄存器：获得操作数地址。第二次访问主存：获得操作数。

例如：MOV AL , [BX]

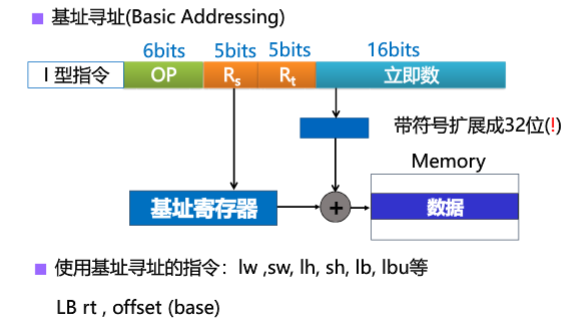
相对寻址

可用于跳转指令。

有效地址为程序计数器PC中的内容+指令中的形式地址。

注意：因为在执行指令的时候，PC会变。这里取的PC的值是下一条将要执行指令的地址。

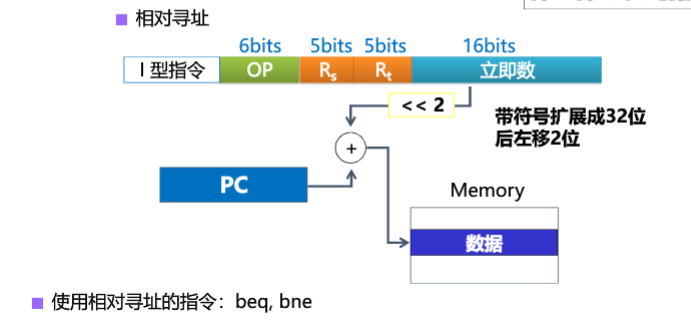
基址寻址

指定一个基址寄存器，与本指令地址无关。

例如：MOV AX ,32[B]

变址寻址

MOV AX , 32[SI]

可以用在循环中。

和基址寻址的不同点是SI是可以修改的。基址B是不可修改的。

指令格式设计

  • 根据指令数量的要求是否支持操作码扩展，确定操作码字段的位数
  • 根据对操作数的要求确定地址码字段的个数
  • 根据寻址方式的要求，为每个地址码字段确定寻址方式字段位数
  • 确定采用定长指令还是变长指令

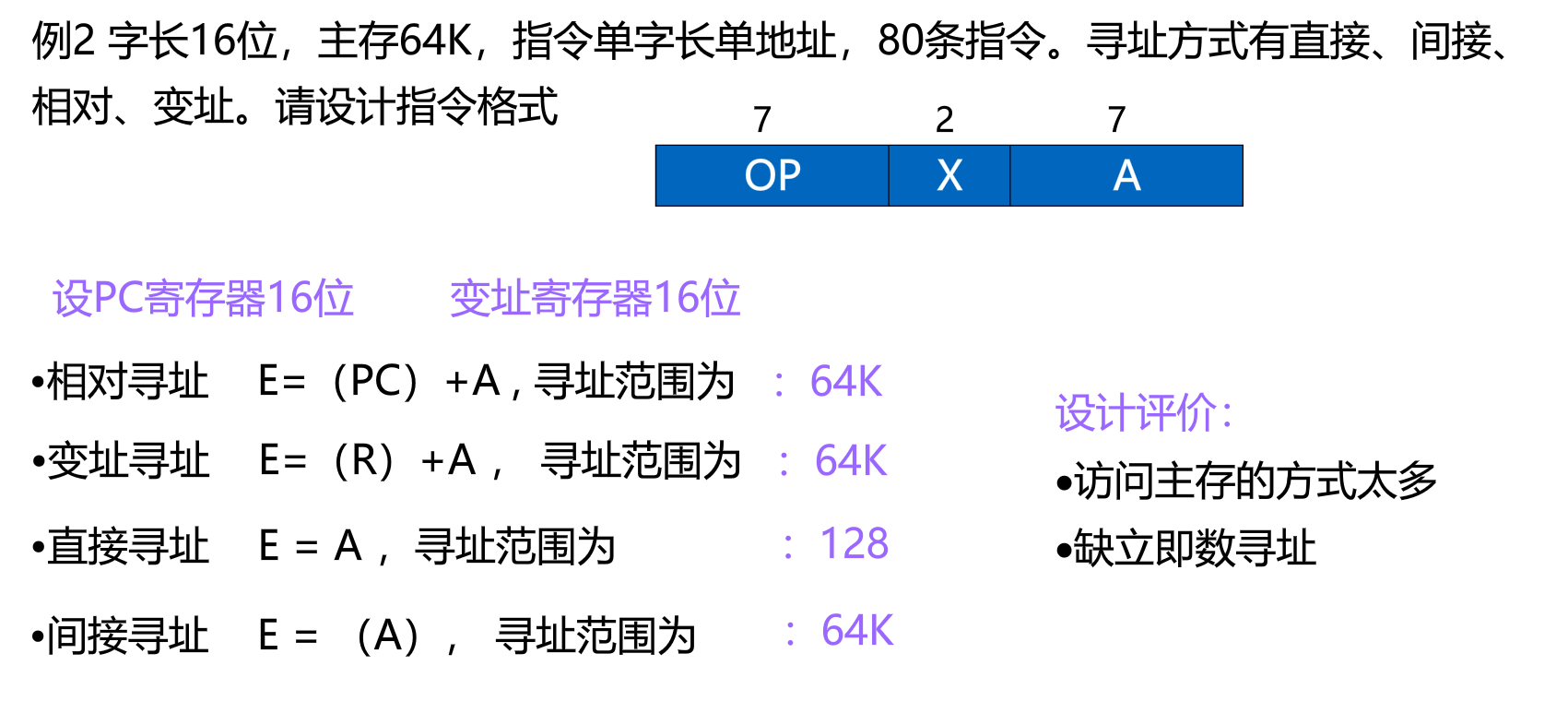
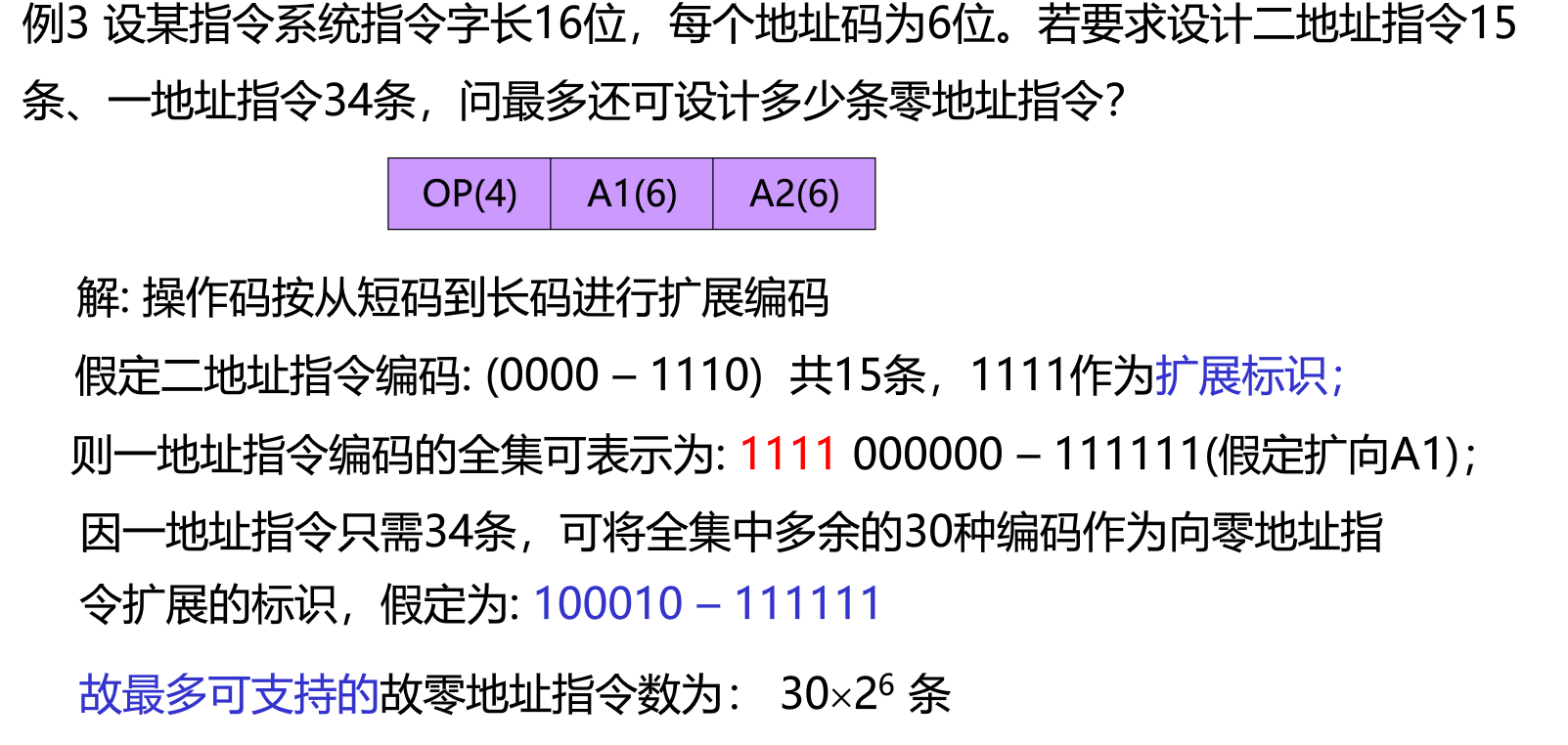
例题：

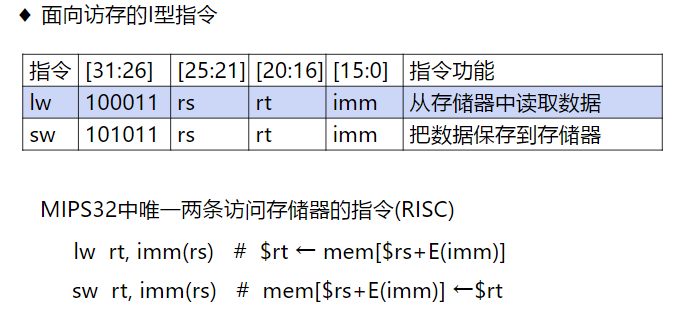
MIPS指令概述

只有三种指令格式

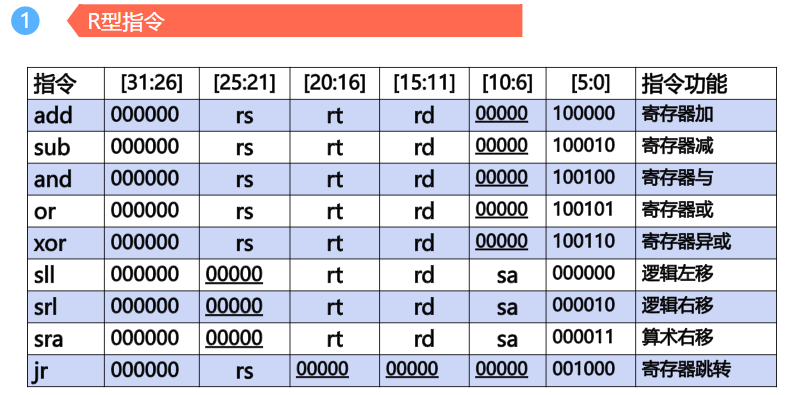
  • R型指令

操作数只能来自寄存器，运算结果也只能存入寄存器。是RR型指令

如果表示移位运算，则表示对Rt的内容进行移位，所移位数有shamt确定。

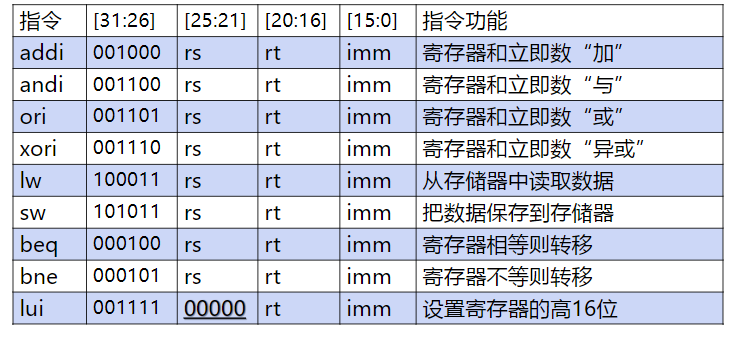
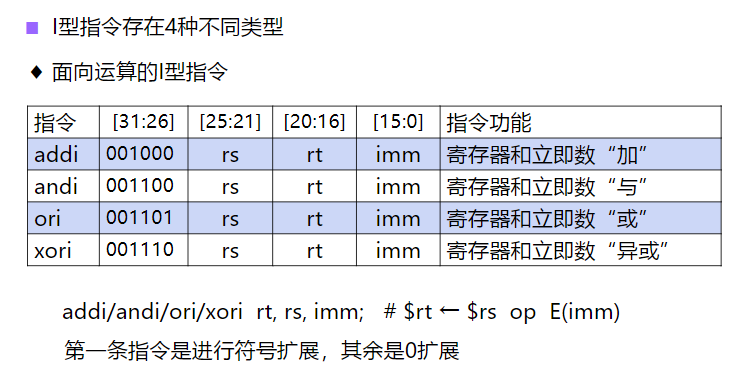
  • I型指令

立即数指令。

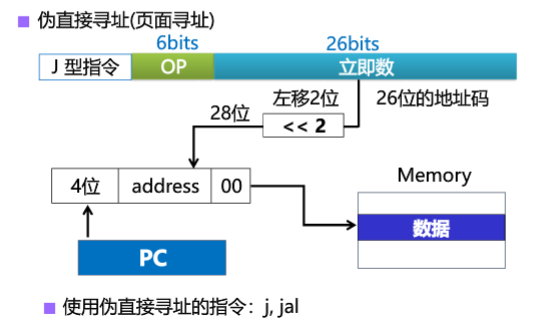
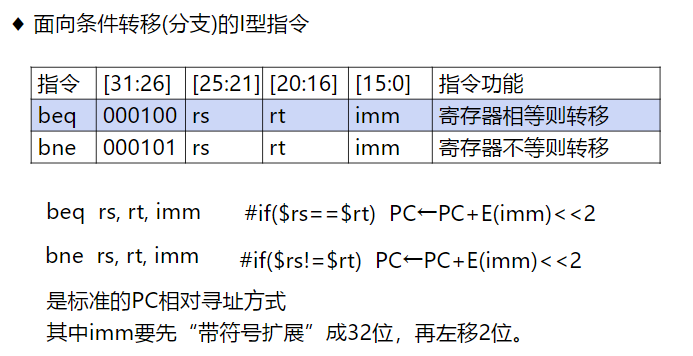
  • J型指令

无条件转移指令。无条件转移的目标地址有PC高4位与26位直接地址左移后的值拼接而成。

注意：不单设寻址方式说明字段。

每一条指令都只有一种寻址方式。

寻址方式

立即数寻址

目标寄存器在右边，源寄存器在左边 和汇编语言恰好相反？？？

image-20191224210907954

寄存器直接寻址

基址寻址

相对寻址

MIPS指令详解

R型指令

三种不同类型

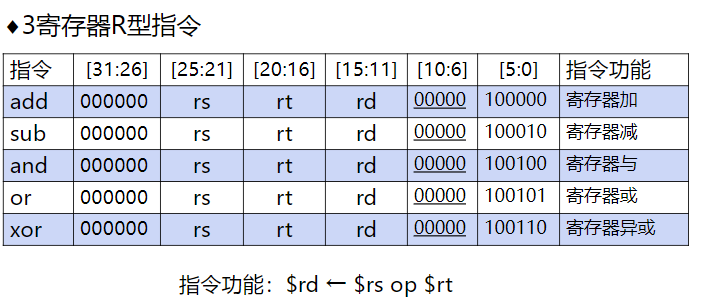
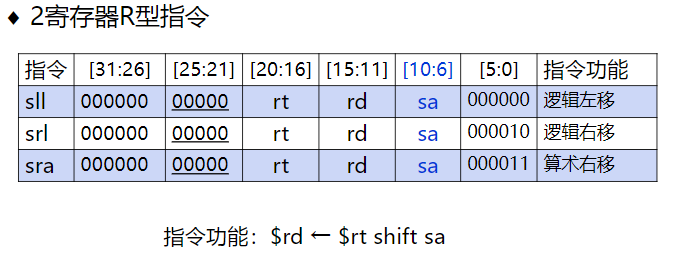
I型指令

J型指令

发表于 更新于 分类于 ，

运算方法和运算器

定点数运算及溢出检测

在机器当中采用补码进行运算。

补码加法：[X＋Y]补= [X]补＋[Y]补 （mod M）

补码减法：[X−Y]补 = [X]补＋[−Y]补 = [X]补−[Y]补

1、这就意味着对所有的数进行运算，都要将其变成补码的形式后再进行运算。
2、得到的答案也是补码，再进行补码转原码。

在硬件的角度考虑：要想使用加法器去实现减法操作，就需要求出[−Y]补

求补公式：[−Y]补= [ [Y]补 ]补

数溢出的概念及其判断方法

溢出：运算结果超出了某种数据类型的表示范围。

溢出和进位的区别：

  1. 溢出是错误，进位不是错误（进位是在运算范围内！溢出就是计算错误）
  2. 溢出是有符号数相加发生的错误: 如 两个正数相加=负数，两个负数相加=正数； 进位是无符号数运算结果超出范围。

溢出是针对有符号数而言的。只有当正+正=负或者负+负=正的时候就表示溢出。如两个操作数符号相同而运算结果的符号与之相反时OV（溢出位）=1，反之，OV=0。

进位是针对无符号数而言的。它的进位就相当于有符号数中的溢出.

通俗一点说就是，即使有符号数相加/相减导致了CF=1也没什么意义，不能说明结果的正确与否。

1、CF的判断

①加法

十进制角度，如果两无符号数相加，结果大于2^n^-1（n为位数），则CF=1，否则CF=0；

二进制角度，如果两无符号数相加，最高位向前有进位，则CF=1，否则CF=0。

②减法

十进制角度，如果两无符号数相减，减数大于被减数（也即结果不在0—2^n^-1内），则CF=1，否则CF=0；

二进制角度，如果两无符号数相减，最高位向前游借位，则CF=1，否则CF=0。

2、OF的判断

①加法

十进制角度，如果两有符号数相加，结果不在-2^(n-1)~2^(n-1)-1内，则OF=1，否则OF=0；

二进制角度，如果两有符号数同号，而相加结果与之异号，则OF=1，否则OF=0。

②减法

十进制角度，如果有符号数相减结果在-2^(n-1)~2^(n-1)-1内，则OF=1，否则OF=0；

二进制角度，如果两个数异号，而相减结果与被减数符号相反，则OF=1，否则OF=0。

溢出的检测：

1、对操作数和运算结果的符号进行检测：正+正的运算结果的符号位一定是正

2、对最高数据位进位和符号位进位进行检测：
正+正的符号位不进位，但是当最高位数据位进位的时候就会顶到符号位上。
负+负的符号位进位，当最高位数据位进位恰好把符号位修改回来。但是最高位数据位不进位就会导致符号位错误。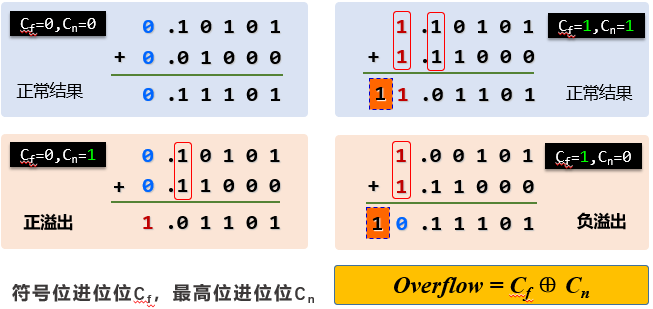

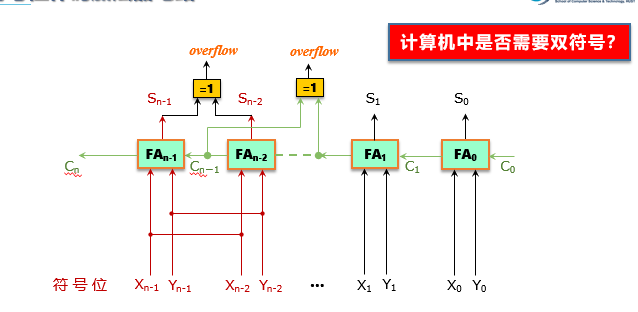
双符号位的溢出检测：

3、变形补码（也叫模4补码）：把两个数的符号位放在一起，即每个参与运算的数据都有两个符号位（00表示正数、11表示负数）

 一个符号位只能表示正、负两种情况，当产生溢出时，符号位的含义就会发生混乱。如果将符号位扩充为两位，其所能表示的信息量将随之扩大，既能检测是否溢出，又能指出结果的符号。在双符号位的情况下，把左边的符号位叫做真符因为它代表了该数真正的符号，两个符号位都作为数的一部分参加运算。这种编码又称为变形补码。
双符号位的含义如下：

  • S1S2=00 结果为正数，无溢出
  • S1S2=01 结果正溢
  • S1S2=10 结果负溢
  • S1S2=11 结果为负数，无溢出

​

无符号数运算的溢出判断（其实是没有溢出的问题，就是借位的问题）

1、无符号数加法的溢出可用ALU的进位表示

2、无符号数减法的溢出可用带加/减功能的ALU的进位取反后表示(意思是向最高位的上一位借位)

定点数补码加、减运算器设计

补码串行加法器

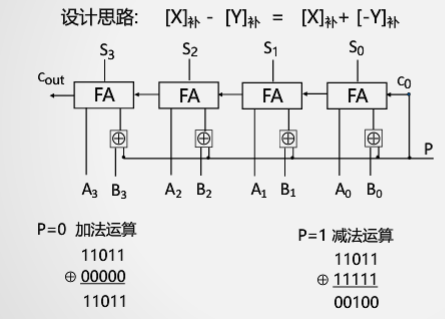
有符号溢出检测方是中第一种：正+正=负

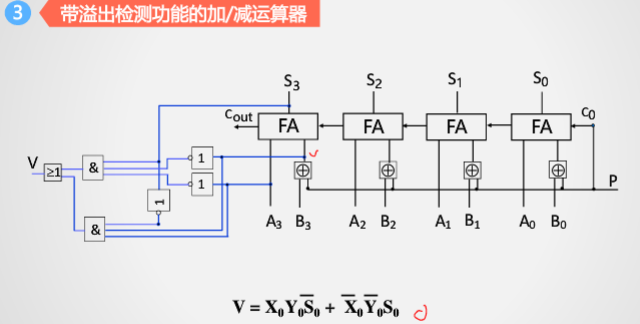
有符号溢出检测方法是第二种：符号位进位和最高位进位异或

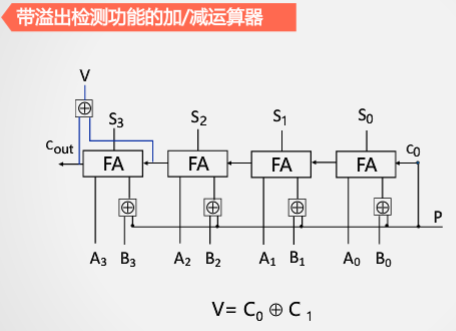
有符号溢出检测是第三种：双符号位

无符号溢出检测：无符号溢出就是数据放不下，故这里需要考虑的是最高位的进位

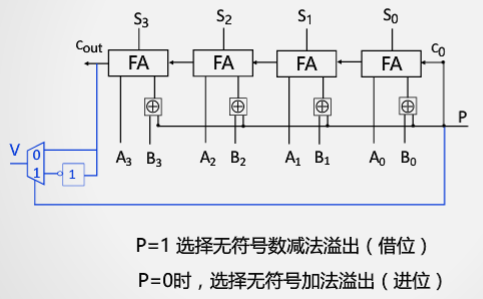
思考：有符号和无符号加法器有什么区别？

A：无符号加减法不存在溢出问题，只是将进位或借位存储在CF中。
机器不知道你进行的运算是否有符号，如果你进行的是有符号运算，你需要查看OF，否则不需要。
所以，溢出不溢出，是由程序员判断的，机器不知道。
但是无符号的“溢出”和有符号的不一样。

串行进位的效率

要等前一个数的进位。

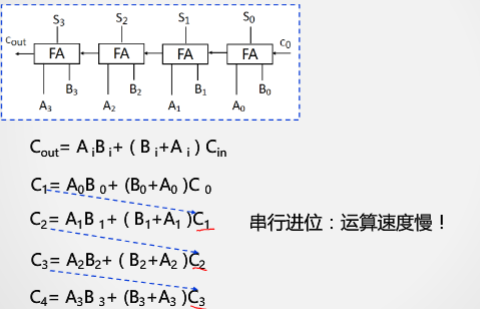
串行加法器的时间延迟

n个全加器延迟，考虑片内并行性，2n+1个门电路延迟。（一个全加器是3个门电路延迟）

并行进位加法器

把串行进位的进位位带入，就可以消除串行进位的进位位要等待的时间。加快运算

然后将带入的算式添加到并行进位运算器中：

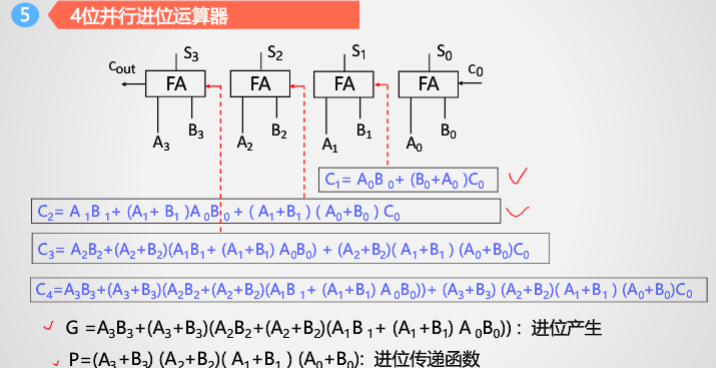
将多个并行加法器连接在一起，构建多位串行进位的并行进位加法器

将多位数的数据拆分，并行进行加法：A15-12等

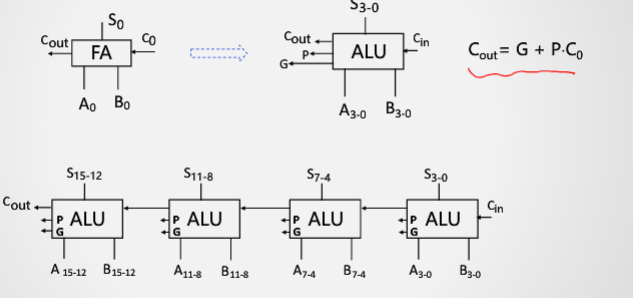
但是，这样存在一个问题：依旧需要串行等待。仿照上述方法，将进位打破

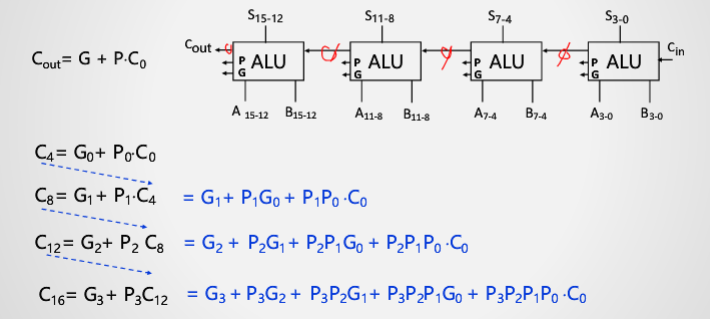
进行到这一步。只需要将P1到P3和G1到G3的值计算得到，就可以完全进行并行进位。

于是，得到的电路图为：

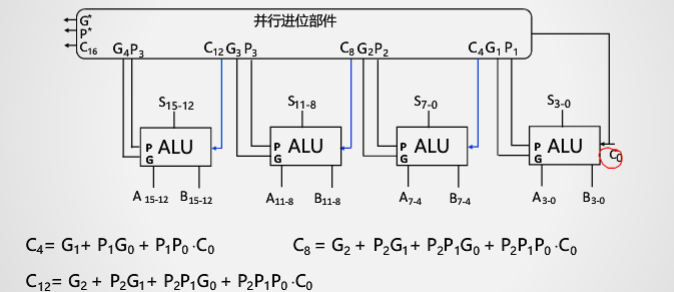
电路延迟示例

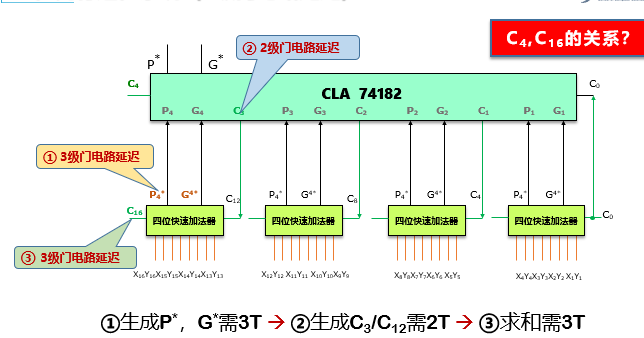
16位先行进位系统（8级门电路延迟）

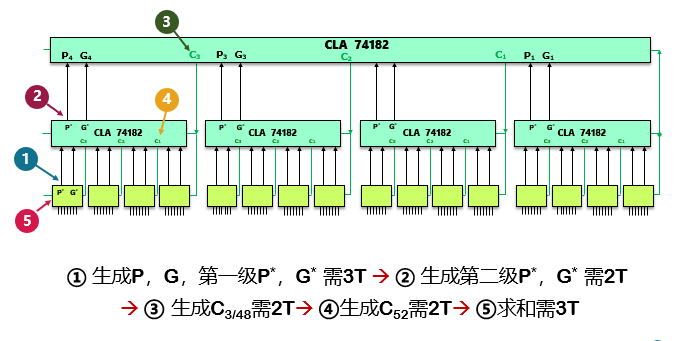
64位先行进位系统（12级门电路延迟）

image-20191228102314643

原码一位乘法

移位

只针对补码而言

**算术左移和逻辑左移的效果是一样的,效果都是*2
逻辑右移最高位补0,算术右移最高位补符号位.**算术右移的效果是/2

逻辑左移=算数左移，右边统一添0

逻辑右移，左边统一添0

算数右移，左边添加的数和符号有关

设计

从手工计算的二进制乘法，可以得到最右边一位是可以直接输出的，故可以每次左移一位，输出的最右边的一位放置在乘法数上（因为0.101在1进行乘法运算后就没用了，可以移动为00.10，于是最左边的0可以用来放置FA循环累加的部分积—最右边的数0）

补码一位乘法

补码和真值的转换公式

$$
设[X]补=X_0.X_1X_2……X_n\
当X>=0,X_0=0,[X]补=0.X_1X_2……X_n=\sum{i=1}^{n}X_i2^{-i}=X\
当X<0,X_0=1,[X]补=1.X_1X_2……X_n=2+X\
所以：\
X=1.X_1X_2……X_n-2=-1+0.X_1X_2……X_n=-1+\sum{i=1}^{n}X_i2^{-i}\
X=-X_0+\sum{i=1}^{n}X_i*2^{-i}
$$

补码的右移

在补码运算的机器中，一个数不论其正负，连同符号位向右移一位，符号位保持不变，就等于乘1/2.
$$
X=-X_0+\sum_{i=1}^{n}X_i2^{-i}\
1/2X=-1/2X_0+1/2\sum_{i=1}^{n}X_i2^{-i}\
=-X_0+1/2\sum_{i=0}^{n}X_i*2^{-(i+1)}\
补码形式：[1/2X]_补=X_0.X_0X_1X_2……X_n
$$

补码乘法规则

$[XY]_补 ≠ [X]_补[Y]_补$

$[XY]_补 = [X]_补Y$

原码乘法的主要问题是符号位不能参加运算，单独用一个异或门产生乘积的符号位。故自然提出能否让符号数字化后也参加乘法运算，补码乘法就可以实现符号位直接参加运算。

乘法运算器设计

原码一位乘法器设计

  • 作完加法，一定移位
  • n次加法
  • 符号位单独计算

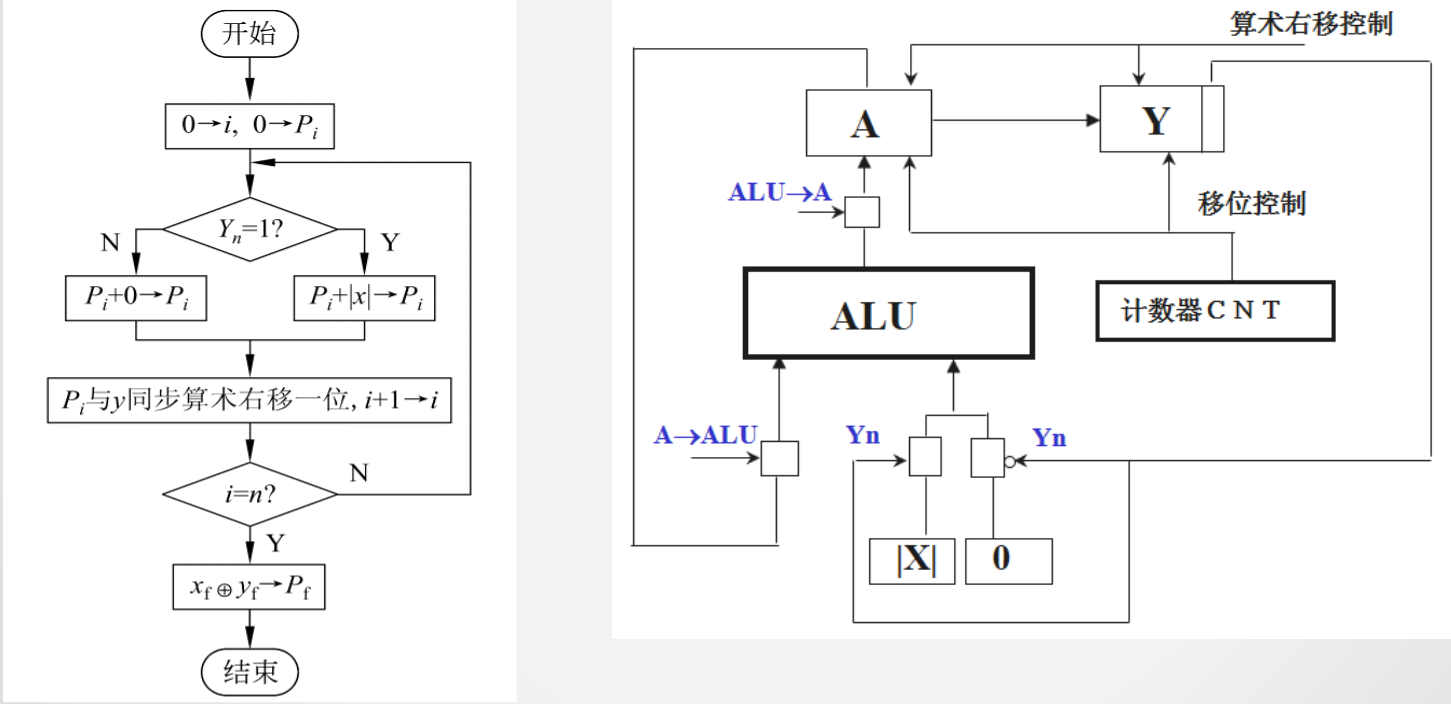
核心运算

累加 ∑ = ∑ + 0 ∑ = ∑ + X

逻辑右移 ∑ = ∑ / 2

分支合并

累加 ∑ = ∑+YnX 节约多路选择器

减少寄存器访问

∑ = (∑ +YnX)/2

先移位再锁存，提升速度

运算计数控制

简单状态机控制，计数器比较

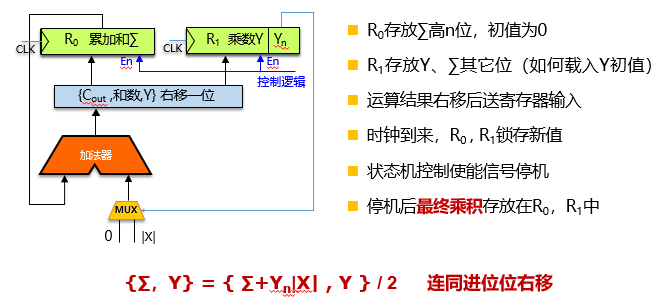
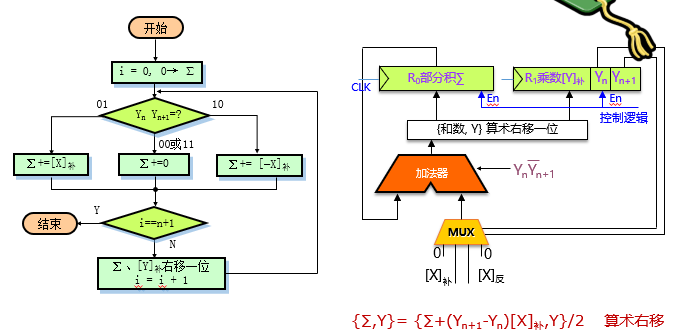
补码一位乘法设计

  • n+1次加法
  • 符号位参与运算
  • 不需要单独计算符号位

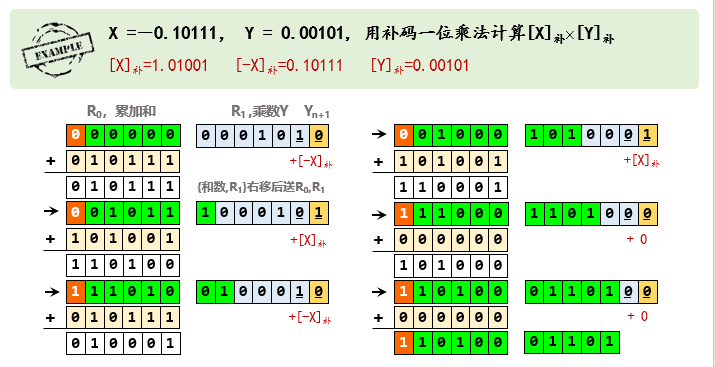
例子:

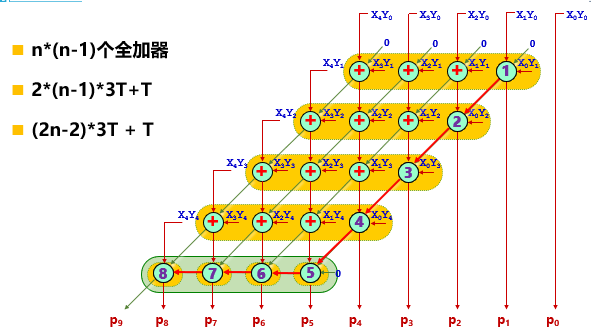
阵列乘法器设计

阵列乘法器的设计目的是为了避免原码一位乘法器中不断循环累加造成的时间浪费

阵列包括了：与门阵列和FA阵列

横向进位阵列乘法器时延分析：

每一行加法器都存在串行进位的关系
6必须等到5计算后才能接着计算（6接收的是5的运算值，把它当作x、y）

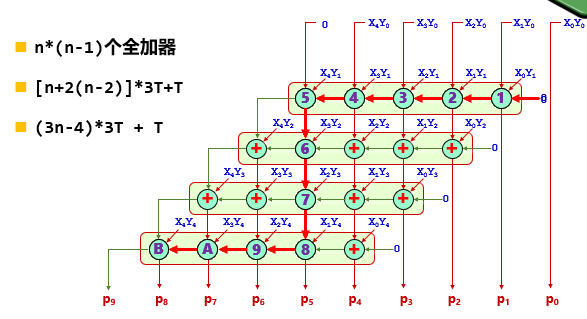
斜向进位阵列乘法器时延分析

将进位送入下一级后，同级的FA之间就不存在串行关系。原因在于：1的进位值对P2产生影响，故1的进位值送入左边还是下一级的2都不会对结果产生影响。

最后一行是串行FA。因为没有下一级送进位了，故只能串行送。

定点数除法

恢复余数除法（绝对值）

当余数为正数：够减，商上1，余数左移一位，再与除数做减法比较

当余数为负数：不够减，商上0
1、加除数恢复成原来的值，将余数左移一位，再与除数做减法比较

重复直至商满足要求。

因为要恢复余数，所以运算步数是不确定的。

上商是根据余数是否>0

加/减交替除法（不恢复余数法）

当余数小于0的时候，不需要恢复余数，余数左移+y。

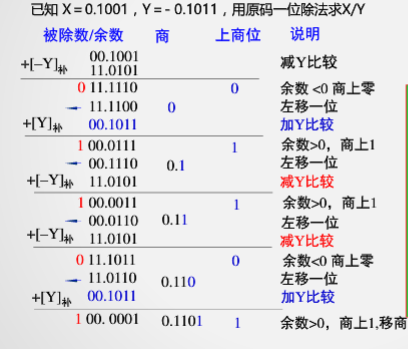
上商是根据左移出的哪位来上的。

浮点数加减运算

浮点数规格化：把一个浮点数转化成指定的格式。

尾数规格化：00.1xxxxx或者11.0xxxxx

步骤

1、对阶
将两个数的阶码转化成一样大小。这样有一个数的尾数将会发生改变

2、尾数的运算
将对阶后的尾数进行加减运算

3、尾数规格化处理
对加减运算后的尾数进行规格化处理，同时阶码也改变了

4、舍入
0舍1入。如果没有丢掉有效数字，就不需要舍入。

5、浮点数的溢出处理
因为是双符号数，溢出规则同双符号数的溢出规则。

上溢：超出所能表示的最大正数
下溢：超出所能表示的最小负数

发表于 更新于 分类于 ，

计算机数据表示

数制和编码

进制转换

真值和机器数

机器数是将符号”数字化”的数，是数字在计算机中的二进制表示形式。因为有符号占据一位，数的形式值就不等于真正的数值，带符号位的机器数对应的数值称为机器数的真值。 例如二进制真值数-011011，它的机器数为 1011011。

BCD码

BCD码(Binary-Coded Decimal)，亦称为二进码十进制数或二-十进制代码。用4位二进制数来表示1位十进制数中的0～9这10个数字，是一种二进制的数字编码形式，用二进制编码的十进制代码。BCD码这种编码形式利用了四个位元来储存一个十进制的数码，使二进制和十进制之间的转换得以快捷的进行。

  • 有权码：8421码，2421码，5421码
  • 无权码：余3码，余3循环码，格雷码

为什么使用BCD码：这种编码技巧最常用于会计系统的设计里，因为会计制度经常需要对很长的数字串作准确的计算。相对于一般的浮点式记数法，采用BCD码，既可保存数值的精确度，又可免去使计算机作浮点运算时所耗费的时间。此外，对于其他需要高精确度的计算，BCD编码亦很常用。

8421码

8421 BCD码是最基本和最常用的BCD码，它和四位自然二进制码相似，各位的权值为8、4、2、1，故称为有权BCD码。和四位自然二进制码不同的是，它只选用了四位二进制码中前10组代码，即用0000~1001分别代表它所对应的十进制数，余下的六组代码不用。如十进制数8的BCD码是1000。

5421码

  5421 BCD码是有权BCD码，从高位到低位的权值分别为5、4、2、1。

​ 数码6可以用0110和1100表示

2421码

  2421 BCD码为有权BCD码，从高位到低位的权值分别为2、4、2、1。

余3码

无权码，是对9的补码

  余3码是8421 BCD码的每个码组加3(0011)形成的。常用于BCD码的运算电路中。

字符与字符串

字符编码ASCII码

可以表示数字、大小写字母和一定数量的专用符号（#等）

汉字的编码

机器数及其特点

原码

原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:

[+1]原 = 0000 0001

[-1]原 = 1000 0001

反码

反码的表示方法是:

正数的反码是其本身

负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.

[+1] = [00000001]原 = [00000001]反

[-1] = [10000001]原 = [11111110]反

补码

补码的表示方法是:

正数的补码就是其本身

负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

补码的模是最高位所在的权重。例如32位字长的数据的补码的模就是2的32次方。

换言之：负数的补码=模+负数。

[+1] = [00000001]原 = [00000001]反 = [00000001]补

[-1] = [10000001]原 = [11111110]反 = [11111111]补

移码

移码通常用于表示浮点数的阶码。移码只用于表示整数。

移码的表示方法是：

数值位与补码相同，符号位与补码相反

总结

整数类型 原码 反码 补码 移码
正整数 0+本身 0+本身 0+本身 补码符号位取反
负整数 1+本身 1+各位取反 反码加1 补码符号位取反
小数类型 原码 反码 补码
正小数 0+小数位 0+小数位 0+小数位
负小数 1+小数位 1+小数位取反 反码加1

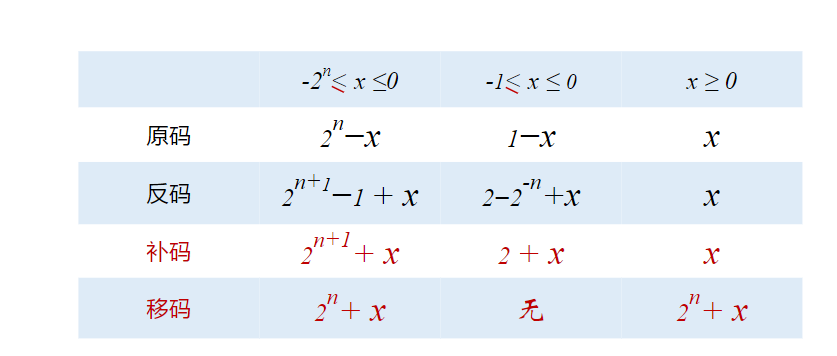
当0的反码有两种：00000或者11111。但是0的补码就只有一种00000（11111+1=00000）。

定点与浮点数据表示

定点

表示定点小数和整数。要求是小数点的位置是固定的，这样就可以不用在字长中表示小数点的位置，就可以利用字长表示更多的有效数字位。

缺点是：定点数的数据的表示范围有限。

以原码为例：

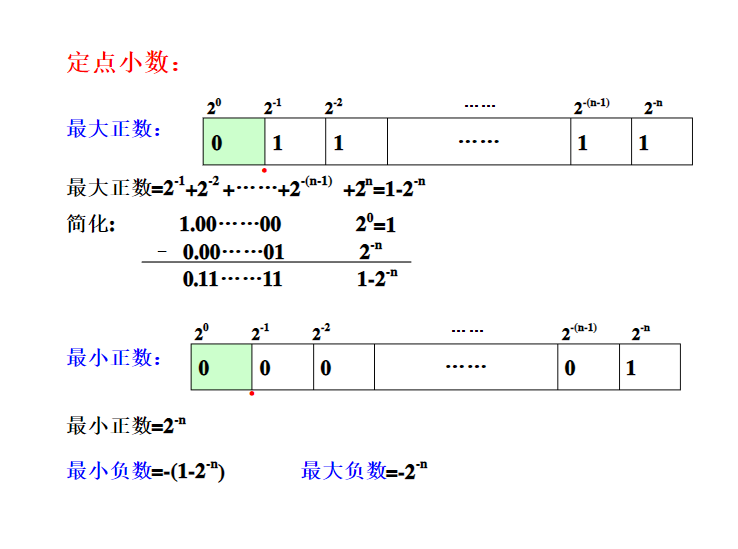
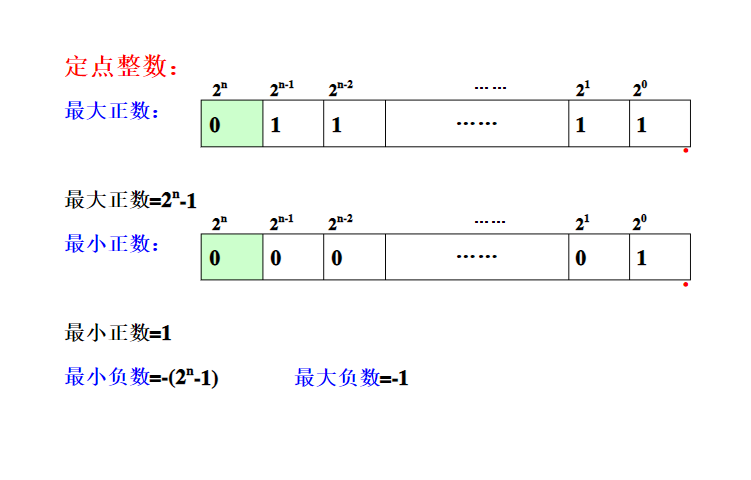
以补码为例：原码的定点小数最小负数为1.1111111其补码表示为1.000000（-1)

​ 原码的定点整数最小负数为11111111其补码表示为1000000（-2的n次方）

定点数的运算

浮点数

浮点数表示为：N = r^E^ × M

式子里面r是浮点数阶码的底在计算机中是隐含的，通常情况下r=2。E和M都是带符号的定点数，E叫做阶码，M叫做尾数。其中E的大小越大，能表示的数范围越大，M的位数越大，数的有效精度越高。

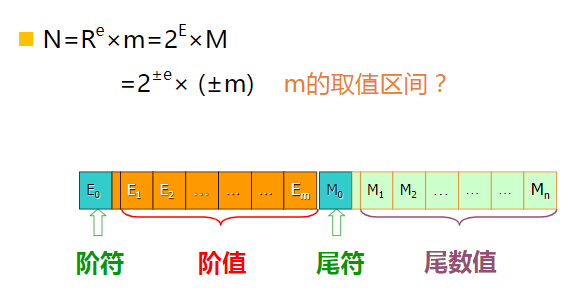
M<1；且同时给出了阶符和尾符。尾数值是小于1的。

IEEE754标准

在IEEE754标准中，此时移码与补码只差符号位的定理不符合

移码是在原码的基础上加的，原码的范围是-127到+127（有+0与-0）
阶码的范围是1到254，就是说阶码没有0与255的说法（无全0与全1）
IEEE754规定，全1是无穷大，而全1减127就是10000000也就是负0，原码的负0加127后表示的阶码是无穷大
IEEE754规定，全0是非规范数，那么全0是怎么加出来的呢，就是原码的10000001
-127·-1~-0·+0·+127
（-1变全0非规范数）·（-2变1）·（-127变126）·（+0变127）·（+127变254）·（-0变255无穷大）

注意只有一个符号位

浮点数省略了基数和阶码的符号位；注意：尾码的符号位由符号位S表示。

需要注意的是，规格化后的尾数是省略了1.的（M表示的就是1.M）

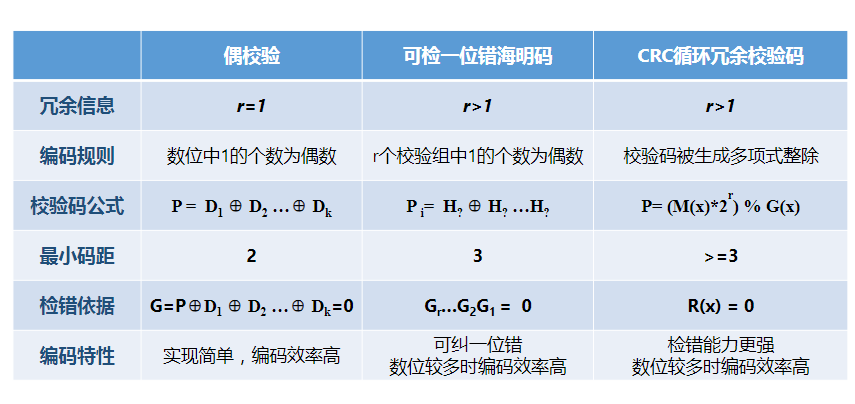
数据校验的基本原理

增加冗余码（校验位）

码距：同一个编码中，任意两个合法编码之间不同二进制位数的最小值。
例如：0011与0001的码距是1，一位错误时无法识别（都在编码中，无法识别是否错误）

校验码中增加冗余项是为了增大码距。

img

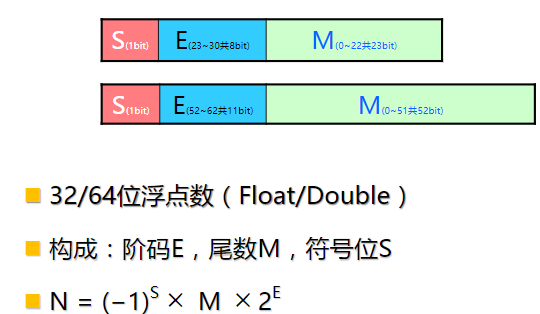
奇偶校验

奇校验：编码规则是整个校验码（包含有效信息和校验位）中的1的个数为奇数个。

同理：偶校验。

实现：校验位只有1位。编码效率高。

错误部分可检测出来。无纠错能力。其码距为2.

改进奇偶校验

1、双向奇偶校验
目标情况：
改进的奇偶校验——目标情况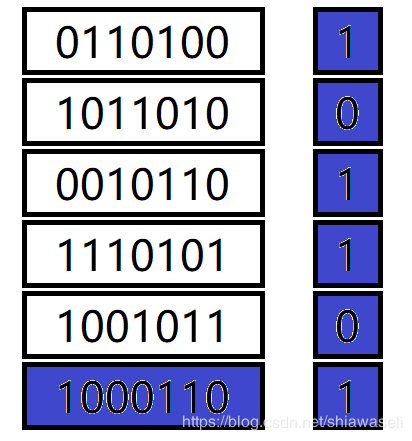
检错分析：
改进的奇偶校验——检错分析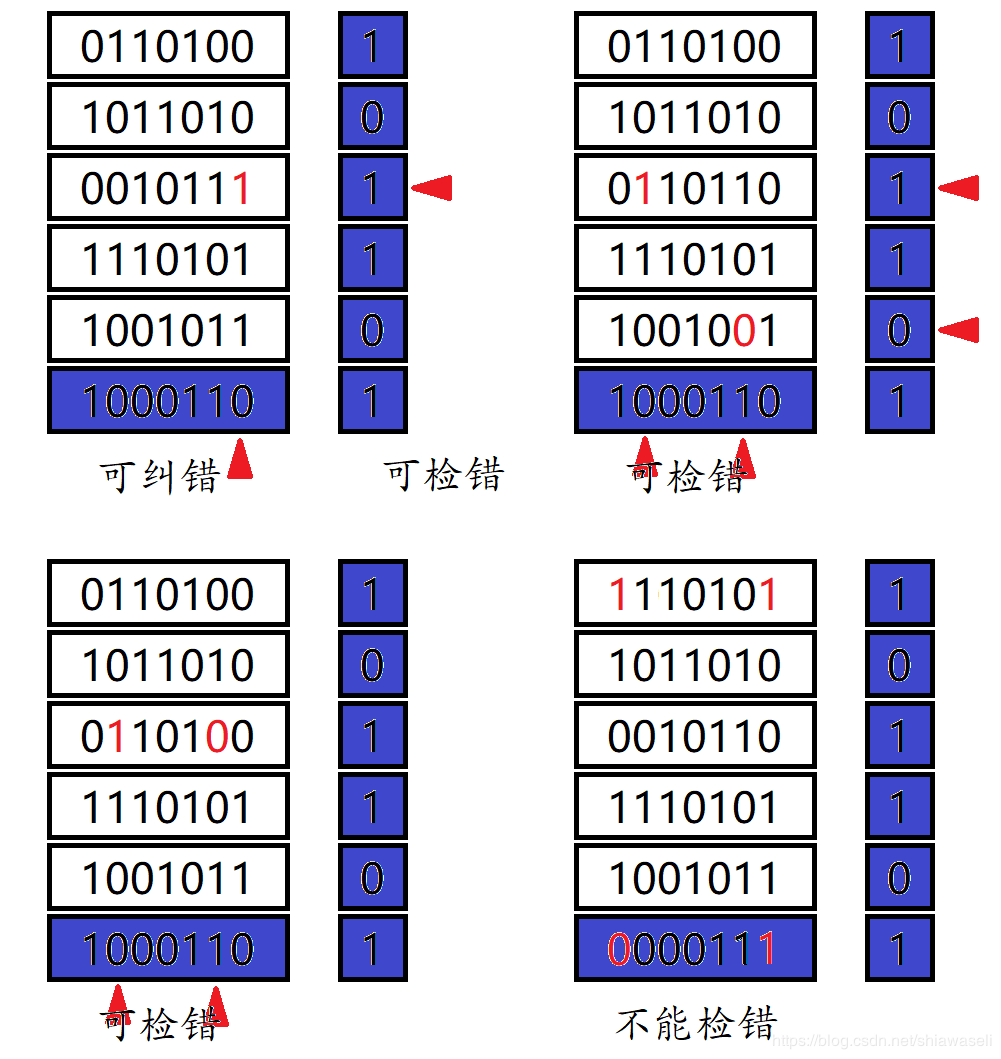
（1）可纠正 1 位错误
（2）可检测出某行（列）上的奇数个错误
（3）可检出部分偶数个错误的情况
（4）不能检测出错码分布在矩形 4 个顶点上的错误

一般在同步传输方式中常采用奇校验，异步传输方式中常采用偶校验

CRC校验

接受方提前获得生成多项式，对CRR校验后的数据进行模2除运算。如果余数不是0，就意味着出现了编码错误。

根据余数，还可以判断具体错误的位置。

设CRC码 N 位，其中数据位 k 位，校验位 r 位（冗余位）

​ N = k + r ≤ 2^r^ − 1 （2r个余数，0表示正确，N位中的每一位出错余数皆不同）

生成多项式

生成多项式特征

  • 任意位发生错误都应使余数不为0
  • 不同位发生错误余数不同
  • 余数左移一位继续作模2除，应使余数循环，循环周期 N=k+r ？

CRC校验原理

其实很简单的问题，其根本思想就是先在要发送的帧后面附加一个数（这个就是用来校验的校验码，但要注意，这里的数也是二进制序列的，下同），生成一个新帧发送给接收端。当然，这个附加的数不是随意的，它要使所生成的新帧能与发送端和接收端共同选定的某个特定数整除（注意，这里不是直接采用二进制除法，而是采用一种称之为“模2除法”）。到达接收端后，再把接收到的新帧除以（同样采用“模2除法”）这个选定的除数。因为在发送端发送数据帧之前就已通过附加一个数，做了“去余”处理（也就已经能整除了），所以结果应该是没有余数。如果有余数，则表明该帧在传输过程中出现了差错。

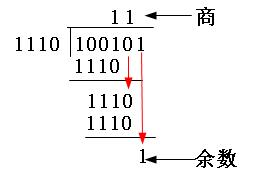
“模2除法”与“算术除法”类似，但它既不向上位借位，也不比较除数和被除数的相同位数值的大小，只要以相同位数进行相除即可。模2加法运算为：1+1=0，0+1=1，0+0=0，无进位，也无借位；模2减法运算为：1-1=0，0-1=1，1-0=1，0-0=0，也无进位，无借位。相当于二进制中的逻辑异或运算。也就是比较后，两者对应位相同则结果为“0”，不同则结果为“1”。如100101除以1110，结果得到商为11，余数为1，如图5-9左图所示。如11×11=101，如图5-9右图所示。

CRC校验码计算示例：
现假设选择的CRC生成多项式为G（X） = X4 + X3 + 1，要求出二进制序列10110011的CRC校验码。下面是具体的计算过程：
①将多项式转化为二进制序列，由G（X） = X4 + X3 + 1可知二进制一种有五位，第4位、第三位和第零位分别为1，则序列为11001
②多项式的位数位5，则在数据帧的后面加上5-1位0，数据帧变为101100110000，然后使用模2除法除以除数11001，得到余数。

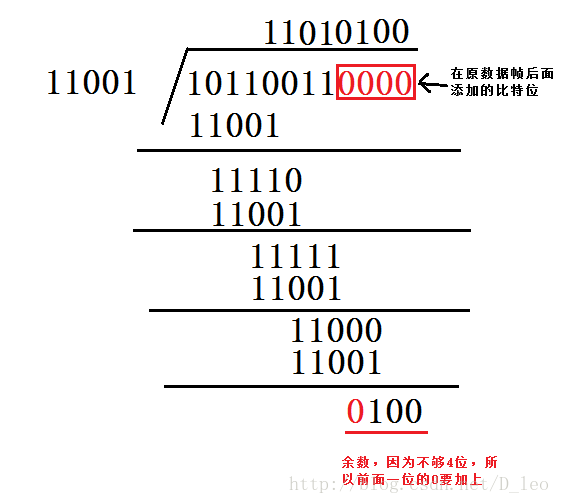
③将计算出来的CRC校验码添加在原始帧的后面，真正的数据帧为101100110100，再把这个数据帧发送到接收端。
④接收端收到数据帧后，用上面选定的除数，用模2除法除去，验证余数是否为0，如果为0，则说明数据帧没有出错。

CRC的纠错

在接收端收到了CRC码后用生成多项式为G(x)去做模2除，若得到余数为0,则码字无误。若如果有一位出错，则余数不为0，而且不同位出错，其余数也不同。可以证明，余数与出错位的对应关系只与码制及生成多项式有关，而与待测字（信息位）无关。【CRC码被G(x)整除，所得的余数与出错位之间有唯一的对应关系。根据这一关系便可立即确定出错位的位置。】

循环校验

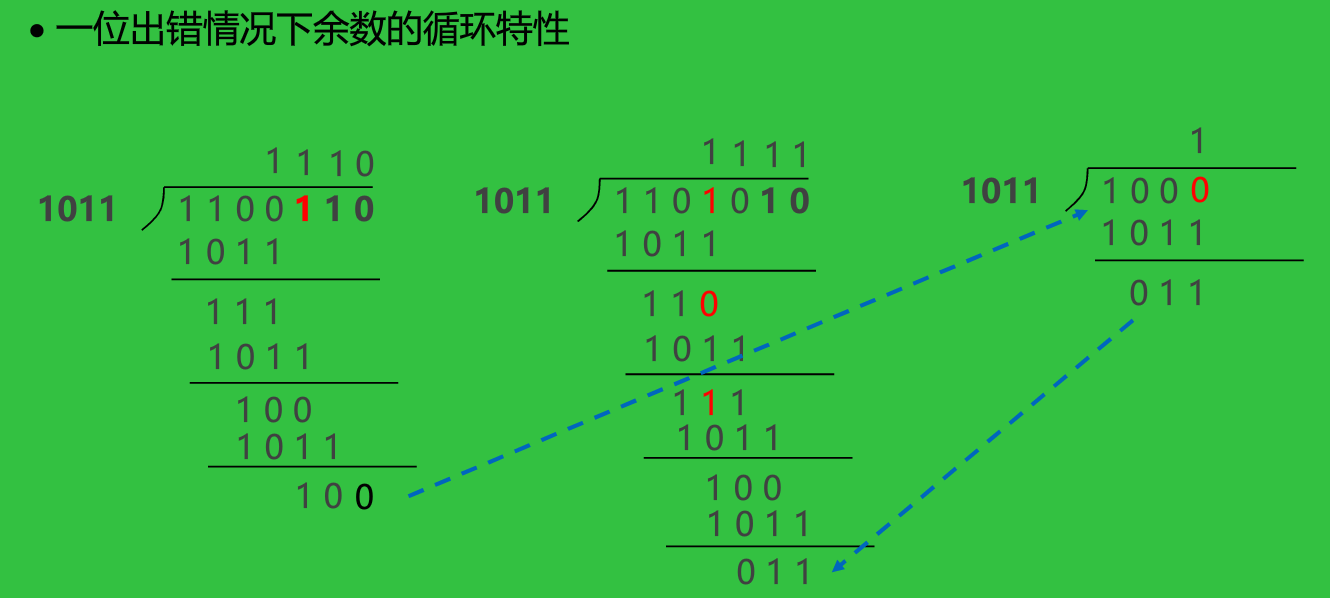
海明校验

海明码的检错、纠错基本思想是将有效信息按某种规律分成若干组，每组安排一个校验位进行奇偶性测试，然后产生多位检测信息，并从中得出具体的出错位置，最后通过对错误位取反（也是原来是1就变成0，原来是0就变成1）来将其纠正。

海明码的编码规则如下：

设有k个校验位Pk,Pk-1,…,P1,n个数据位为Dn-1,Dn-2,…,D1,D0,对应的海明码为Hn+k,Hn+k-1,…,H1,H0,那么：

（1）P1在海明码的位置，即Hj=Pi,且,数据位则依程序从低到高占据海明码中剩下的位置。

（2）海明码中任意一位都是由若干个校验码来检验的，其对应关系如下：被校验的海明位的下标等于所有参与校验该位的检验位的下标之和，而校验位由自身校验。

步骤：

1、计算检验位的位数

假设用N表示添加了校验码位后整个信息的二进制位数，用K代表其中有效信息位数，r表示添加的校验码位，它们之间的关系应满足：N=K＋r≤2^r^－1。（一位纠错功能）

原理是分成r组进程奇偶校验就会产生r位检错信息，可指出2^r^种状态。其中一种状态是无错，其余状态就可以指出哪位出错

如K=5，则要求2^r^-r≥5+1=6，根据计算可以得知r的最小值为4，也就是要校验5位信息码，则要插入4位校验码。如果信息码是8位，则要求2^r^-r≥8+1=9，根据计算可以得知r的最小值也为4。

2、确定校验码位置

校验码必须是在2^n^次方位置，如第1、2、4、8、16、32，……位（对应2^0^、2^1^、2^2^、2^3^、2^4^、2^5^，……，是从最左边的位数起的），这样一来就知道了信息码的分布位置，也就是非2^n^次方位置，如第3、5、6、7、9、10、11、12、13，……位（是从最左边的位数起的）。这种分组关系是因为任何数都可以分成2的幂次方相加的形式

假设现有一个8位信息码，即b1、b2、b3、b4、b5、b6、b7、b8，它需要插入4位校验码，即p1、p2、p3、p4，也就是整个经过编码后的数据码（称之为“码字”）共有12位。根据以上介绍的校验码位置分布规则可以得出，这12位编码后的数据就是p1、p2、b1、p3、b2、b3、b4、p4、b5、b6、b7、b8。

3、确定校验码

每个校验位的值代表了代码字中部分数据位的奇偶性（最终要根据是采用奇校验，还是偶校验来确定），其所在位置决定了要校验的比特位序列。总的原则是：第i位校验码从当前位开始，每次连续校验i（这里是数值i，不是第i位，下同）位后再跳过i位，然后再连续校验i位，再跳过i位，以此类推。最后根据所采用的是奇校验，还是偶校验即可得出第i位校验码的值。

校验码的具体计算方法如下：

p1（第1个校验位，也是整个码字的第1位）的校验规则是：从当前位数起，校验1位，然后跳过1位，再校验1位，再跳过1位，……。这样就可得出p1校验码位可以校验的码字位包括：第1位（也就是p1本身）、第3位、第5位、第7位、第9位、第11位、第13位、第15位，……。然后根据所采用的是奇校验，还是偶校验，最终可以确定该校验位的值。

p2（第2个校验位，也是整个码字的第2位）的校验规则是：从当前位数起，连续校验2位，然后跳过2位，再连续校验2位，再跳过2位，……。这样就可得出p2校验码位可以校验的码字位包括：第2位（也就是p2本身）、第3位，第6位、第7位，第10位、第11位，第14位、第15位，……。同样根据所采用的是奇校验，还是偶校验，最终可以确定该校验位的值。

p3（第3个校验位，也是整个码字的第4位）的校验规则是：从当前位数起，连续校验4位，然后跳过4位，再连续校验4位，再跳过4位，……。这样就可得出p4校验码位可以校验的码字位包括：第4位（也就是p4本身）、第5位、第6位、第7位，第12位、第13位、第14位、第15位，第20位、第21位、第22位、第23位，……。同样根据所采用的是奇校验，还是偶校验，最终可以确定该校验位的值。

p4（第4个校验位，也是整个码字的第8位）的校验规则是：从当前位数起，连续校验8位，然后跳过8位，再连续校验8位，再跳过8位，……。这样就可得出p4校验码位可以校验的码字位包括：第8位（也就是p4本身）、第9位、第10位、第11位、第12位、第13位、第14位、第15位，第24位、第25位、第26位、第27位、第28位、第29位、第30位、第31位，……。同样根据所采用的是奇校验，还是偶校验，最终可以确定该校验位的值。

4、实现校验和纠错

从表中可以得出以下两个规律：

  • 所有校验码所在的位是只由对应的校验码进行校验，如第1位（只由p1校验）、第2位（只由p2校验）、第4位（只由p3校验）、第8位（只由p4校验）、第16位（只由p5校验），……。也就是这些位如果发生了差错，影响的只是对应的校验码的校验结果，不会影响其它校验码的校验结果。这点很重要，如果最终发现只是一个校验组中的校验结果不符，则直接可以知道是对应校验组中的校验码在传输过程中出现了差错。
  • 所有信息码位均被至少两个校验码进行了校验，也就是至少校验了两次。查看对应的是哪两组校验结果不符，然后根据上表就可以很快确定是哪位信息码在传输过程中出了差错。

海明码校验的方式就是各校验码对它所校验的位组进行“异或运算”

G1=p1⊕b1⊕b2⊕b4⊕b5⊕……

G2=p2⊕b1⊕b3⊕b4⊕b6⊕b7⊕b10⊕b11⊕……

G3= p3⊕b2⊕b3⊕b4⊕b8⊕b9⊕b10⊕b11⊕……

G4= p4⊕b5⊕b6⊕b7⊕b8⊕b9⊕b10⊕b11⊕……

G5= p5⊕b12⊕b13⊕b14⊕b15⊕b16⊕b17⊕b18⊕b19⊕b20⊕b21⊕b11⊕b23⊕b24⊕b25⊕b26⊕……

正常情况下（也就是整个码字不发生差错的情况下），在采用偶校验时，各校验组通过异或运算后的校验结果均应该是为0，也就是前面所说的G1、G2、G3、G4，……均为0，因为此时1为偶数个，进行异或运算后就是0；而采用奇校验时，各组校验结果均应是为1。

现在举一个例子来说明，假设传输的海明码为==11==1==0==001==1==1101（一共12位，带高亮的4位就是校验码），从中可以知道它有四个校验组：G1、G2、G3、G4，然而到达接收端经过校验后发现只有G4=1（也就是只有这组校验结果不等于0），通过前面介绍的校验规律可以很快地发现是G4校验组中的p4校位码（也就是整个码字中的第8位）错了（因为只有一组校验结果出现差错时，则肯定只是对应的校验位出了差错），也就是最终的码字变成了：111000001101。

再假设G3、G4两个校验值都不为0，也就是都等于1。通过上表中比较G3、G4两个校验组（注意本示例中码字长度一共才12位，只需要比较前12位）中共同校验的码位可是以很快发现是b8，也就是第12位出现了差错，也就是最终的码字变成了：111000011100。

PS：指错字G1、G2、G3、G4=0000的时候不一定无错！！

如P1、b1、P2三位同时出错，G2和G1依旧是0。

原因是：海明校验还是基于奇偶校验的

ps：一位错和两位错不能由指错字区别！！！

如b1、b2同时出错，与仅b3出错的指错字是一样的：0110

海明码最高一个校验位，被称为总校验位，它的值，是通过对全部数据位和其它全部校验位（不含P13本身）执行偶校验计算求得的。

校验码总结

c语言中的数据存储方式

类型 长度/子节 取值范围 存储方式
char 1 -128~127 有符号二进制补码形式
[signed]char 1 -128~127
unsigned char 1 0~255
short[int] 2 -32768~32768
unsigned short[int] 2 0~65535
int 4 -2147483648~2147483647 定点有符号二进制补码形式
[signed]int 4 -2147483648~2147483647
unsigned int 1 0~4294967295
long[int] 2 -2147483648~2147483647
unsigned long[int] 4 -2147483648~2147483647
unsigned long [int] 4 0~4294967295
float 4 -3.410^38~3.410^38 浮点形式存储
double 8 -1.79810^308~1.79810^308 浮点形式存储
long double 8 -1.79810^308~1.79810^308 浮点形式存储

备注：
short int<=int<=long int<=long long int
float<=double<=long double

int型

  1. 占用4个字节，即：32b，有符号位：从左数第一位。
  2. 取值范围：-2^31^ ~ 2^31^-1。
    原因：0 代表 +0，-0 代表 -2^31^，故负数比整数多一个。
  3. 数据以补码的形式存放在内存中。
  4. 对于+0和-0在内存中的存储方式。

unsigned int型

  1. 占用4个字节，即：32b，无符号位。
  2. 取值范围：0 ~ 2^32^。
  3. 数据以补码的形式存放在内存中。

float型和double型

遵循IEEE745规范。

char型

在内存中以ASCII码的形式存储。

强制类型转换

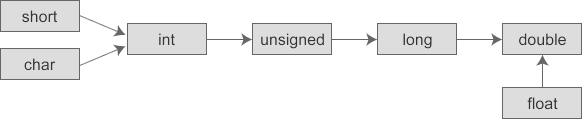
算术运算式中，低类型能够转换为高类型。【一般只是形式上有所改变， 而不影响数据的实质内容， 而较高类型的数据转换为较低类型时则可能有些数据丢失。】

​ a.若两种类型的字节数不同，转换成字节数高的类型

​ b.若两种类型的字节数相同，且一种有符号，一种无符号，则转换成无符号类型

(1) 浮点型与整型

将浮点数(单双精度)转换为整数时，将舍弃浮点数的小数部分， 只保留整数部分。 将整型值赋给浮点型变量，数值不变，只将形式改为浮点形式， 即小数点后带若干个0。注意：赋值时的类型转换实际上是强制的。

(2) 单、双精度浮点型

由于c语言中的浮点值总是用双精度表示的，所以float 型数据只是在尾部加0延长为double型数据参加运算，然后直接赋值。double型数据转换为float型时，通过截尾数来实现，截断前要进行四舍五入操作。

(3) char型与int型

int型数值赋给char型变量时，只保留其最低8位，高位部分舍弃。
char型数值赋给int型变量时， 一些编译程序不管其值大小都作正数处理，而另一些编译程序在转换时，若char型数据值大于127，就作为负数处理。对于使用者来讲，如果原来char型数据取正值，转换后仍为正值;如果原来char型值可正可负，则转换后也仍然保持原值， 只是数据的内部表示形式有所不同。

(4) int型与long型

long型数据赋给int型变量时，将低16位值送给int型变量，而将高16 位截断舍弃。(这里假定int型占两个字节)。

将int型数据送给long型变量时，其外部值保持不变，而内部形式有所改变。

(5) 无符号整数

将一个unsigned型数据赋给一个占据同样长度存储单元的整型变量时(如：unsigned→int、unsigned long→long，unsigned short→short) ，原值照赋，内部的存储方式不变，但外部值却可能改变。

将一个非unsigned整型数据赋给长度相同的unsigned型变量时， 内部存储形式不变，但外部表示时总是无符号的。

PS

名词解释

真值：正号和负号分别用“+”和“-”表示，数据位保持二进制值不变的数据表示方法。

数值数据：计算机所支持的一种数据类型，用于科学计算，常见的数值数据类型包括小数、整数、浮点数数等。

非数值数据：计算机所支持的一种数据类型，一般用来表示符号或文字等没有数值值的数据。

机器数：数据在机器中的表示形式，是正负符号数码化后的二进制数据。

变形补码：用两个二进制位来表示数字的符号位，其余与补码相同。即“00”表示正，“11”表示负。

规格化：将非规格化的数处理成规格化数的过程。规格化数规定尾数用纯小数表示，且真值表示时小数点后第一位不为0（以机器数表示时对小数点后第一位的规定与具体的机器数的形式有关）。

机器零：计算机保存数字的位有限，所能表示最小的数也有范围，其中有一个范围之中的数据无法精确表示，当实际的数据处在这个无法精确表示的数据范围时计算机就将该数作为机器零来处理，因此，计算机中的机器零其实对应的不是一个固定的数，而是一个数据表示范围。

BCD码：用4位二进制数来表示1位十进制数中的0~9这10个数码，即二进制表示的十进制数。

汉字内码：计算机内部存储、处理加工和传输汉字时所用的由0和1符号组成的代码。

码距：一组编码中对应位上数字位不同的最小个数。

奇偶校验：通过检测校验码中1的个数的奇/偶性是否改变来判断数据是否出错的一种数据校验方法。

海明校验：是一种基于多重奇校验且具有检测与纠正错误的校验方法。其基本原理是将有效信息按某种规律分成若干组，每组安排一个校验位进行奇偶测试，就能提供多位检错信息，以指出最大可能是哪位出错，从而将其纠正。

循环冗余校验：是数据通信领域中最常用的一种具有检测与纠正错误能力差错校验码，基利用生成多项式并基于模2运算建立编码规则。

检错：检测被传送的信息中是否发生差错。

纠错：纠正信息在传送或存储过程中所发生的错误。

简要问题

1)为什么计算机中采用二进制?

答：因为二进制具有运算简单和表示简单的优点，除此之外还有可靠和容易实现等特点。

具体来说，是因为：

（1）技术实现简单，计算机是由逻辑电路组成，逻辑电话通常只有两个状态，开关

的接通与断开，这两种状态正好可以用“1”和“0”表示。

（2）简化运算规则：两个二进制数和、积运算组合各有三种，运算规则简单，有利

于简化计算机内部结构，提高运算速度。

（3）适合逻辑运算：逻辑代数是逻辑运算的理论依据，二进制只有两个数码，正好

与逻辑代数中的“真”和“假”相吻合。

（4）易于进行转换，二进制与十进制数易于互相转换。

2)为什么计算机中采用补码表示带符号的整数?

答：采用补码运算具有如下两个特征：

（1）因为使用补码可以将符号位和其他位统一处理，同时，减法也可以按加法来处理，即如果是补码表示的数，不管是加减法都直接用加法运算即可实现。

（2）两个用补码表示的数相加时，如果最高位（符号位）有进位，则进位被舍弃。

这样的运算有两个好处：

（a）使符号位能与有效值部分一起参加运算，从而简化运算规则。从而可以简化运算器的结构，提高运算速度；（减法运算可以用加法运算表示出来。）

（b）加法运算比减法运算更易于实现。使减法运算转换为加法运算，进一步简化计算机中运算器的线路设计。

3)浮点数的表示范围和精确度分别由什么决定?字长一定时浮点数的表示范围与精确度之间有和关系?

答：浮点数的表示范围由阶码的位数决定，精确度由尾数的位数决定。

当机器字长一定时，分给阶码的位数越多，尾数占用的位数就越少，则数的表示范围越大。而尾数占用的位数减少，必然会减少数的有效数位，即影响数的精度。

4)汉字输入码、机内码和字型码在汉字处理过程中各有何作用？

答：汉字输入码、机内码和字型码，分别用于汉字的输入、汉字在计算机内的处理以及汉字的显示和打印。

具体来说，计算机要对汉字信息进行处理，首先要将汉字转换成计算机可以识别的二进制形式并输入到计算机，这是由汉字输入码完成的；汉字输入到计算机后，还需要转换成内码才能被计算机处理，显然，汉字内码也应该是二进制形式。如果需要显示和打印汉字，还要将汉字的内码转换成字形码。

5)在机内码中如何区分两个ASCII码字符和一个汉字?

答：将一个汉字看成是两个扩展ASCII码，使表示GB2312汉字的两个字节的最高位都为1，而每个ASCII码字符中每个字节的最高位为0。这样就能区别一个机内码到底对应一个汉字还是两个西文字符。

6)“8421码就是二进制数”。这种说法对吗？为什么？

答：这种说法是不对的。8421码是一种最简单的有权码，它选取4位二进制数的前10个代码0000～1001分别对应表示十进制数的10个数码。若按权求和，和数就等于该代码所对应的十进制数。

8421码是一种编码方式，用于十进位制与二进制数之间的转换。

而二进制数是用0和1两个数码来表示的数。二者是不同的概念，不能等同。

7)如何识别浮点数的正负？浮点数能表示的数值范围和数值的精确度取决于什么？

答：当采用一般浮点数格式表示浮点数时,阶码和尾数都各包含一位符号位。浮点数的正负由尾数的的符号位决定。当采用IEEE754格式时，通过数符就能判断出浮点数的正负。

浮点数能表示的数值范围和数值的精确度，分别取决于阶码的位数和尾数的位数。

8)简述CRC的纠错原理。

答：发送部件将某信息的CRC码传送至接收部件，接收部件收到CRC码后，仍用约定的生成多项式G(x)去除，若余数为0，表示传送正确；若余数不为0，表示出错，再由余数的值来确定哪一位出错，从而加以纠正。具体的纠错原理如下：

（1）不论错误出现在哪一位,均要通过将出错位循环左移到最左边的一位上时被纠正；

（2）不为零余数的具有循环特性。即在余数后面补一个零除以生成多项目式,将得到下一个余数,继续在新余数基础上补零除以生成多项式,继续该操作，余数最后能循环到最开始的余数。

（3）CRC就是利用不为零余数的循环特性,在循环计算余数的同时，将收到的CRC编码同步移动，当余数循环到等于最左边位出错对应的余数时，表明已将出错的位移到CRC码的最左边,对出错位进行纠错。

（4）继续进行余数的循环计算,并同步移动CRC编码,当余数又回到最开始的值时,纠错后的CRC码又回到了最开始的位置。至此，完成CRC的纠错任务。

发表于 更新于 分类于

创建进程

父进程创建子进程需要用到fork()函数。调用 fork 时，系统将创建一个与当前进程相同的新进程。通常将原有的进程称为父进程，把新创建的进程称为子进程。子进程是父进程的一个拷贝，子进程获得同父进程相同的数据，但是同父进程使用不同的数据段和堆栈段。子进程从父进程继承大多数的属性，但是也修改一些属性，下表对比了父子进程间的属性差异：

继承属性 差异
uid,gid,euid,egid 进程 ID
进程组 ID 父进程 ID
SESSION ID 子进程运行时间记录
所打开文件及文件的偏移量 父进程对文件的锁定
控制终端
设置用户 ID 和 设置组 ID 标记位
根目录与当前目录
文件默认创建的权限掩码
可访问的内存区段
环境变量及其它资源分配

fork调用的一个奇妙之处就是它仅仅被调用一次，却能够返回两次，在父进程中调用一次，在父进程和子进程中各返回一次。它可能有三种不同的返回值：
1）在父进程中，fork返回新创建子进程的进程ID；
2）在子进程中，fork返回0；
3）如果出现错误，fork返回一个负值；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <unistd.h>  
#include <stdio.h>   
int main ()   
{   
    pid_t fpid; //fpid表示fork函数返回的值  
    int count=0;  
    fpid=fork();   
    if (fpid < 0)   
        printf("error in fork!");   
    else if (fpid == 0) {  
        printf("i am the child process, my process id is %d/n",getpid());   
        printf("我是爹的儿子/n");//对某些人来说中文看着更直白。  
        count++;  
    }  
    else {  
        printf("i am the parent process, my process id is %d/n",getpid());   
        printf("我是孩子他爹/n");  
        count++;  
    }  
    printf("统计结果是: %d/n",count);  
    return 0;  
}

运行结果是：

1
2
3
4
5
6
i am the child process, my process id is 5574
 我是爹的儿子
 统计结果是: 1
 i am the parent process, my process id is 5573
 我是孩子他爹
 统计结果是: 1

在语句fpid=fork()之前，只有一个进程在执行这段代码，但在这条语句之后，就变成两个进程在执行了，这两个进程的几乎完全相同，将要执行的下一条语句都是if(fpid<0)……

在fork函数执行完毕后，如果创建新进程成功，则出现两个进程，一个是子进程，一个是父进程。在子进程中，fork函数返回0，在父进程中，fork返回新创建子进程的进程ID。我们可以通过fork返回的值来判断当前进程是子进程还是父进程。

引用一位网友的话来解释fpid的值为什么在父子进程中不同。“其实就相当于链表，进程形成了链表，父进程的fpid(p 意味point)指向子进程的进程id, 因为子进程没有子进程，所以其fpid为0.
fork出错可能有两种原因：
1）当前的进程数已经达到了系统规定的上限，这时errno的值被设置为EAGAIN。
2）系统内存不足，这时errno的值被设置为ENOMEM。
创建新进程成功后，系统中出现两个基本完全相同的进程，这两个进程执行没有固定的先后顺序，哪个进程先执行要看系统的进程调度策略。
每个进程都有一个独特（互不相同）的进程标识符（process ID），可以通过getpid（）函数获得，还有一个记录父进程pid的变量，可以通过getppid（）函数获得变量的值。
fork执行完毕后，出现两个进程。

有人说两个进程的内容完全一样啊，怎么打印的结果不一样啊，那是因为判断条件的原因，上面列举的只是进程的代码和指令，还有变量啊。
执行完fork后，进程1的变量为count=0，fpid！=0（父进程）。进程2的变量为count=0，fpid=0（子进程），这两个进程的变量都是独立的，存在不同的地址中，不是共用的，这点要注意。可以说，我们就是通过fpid来识别和操作父子进程的。
还有人可能疑惑为什么不是从#include处开始复制代码的，这是因为fork是把进程当前的情况拷贝一份，执行fork时，进程已经执行完了int count=0;fork只拷贝下一个要执行的代码到新的进程。

fork进阶知识

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <unistd.h>  
#include <stdio.h>  
int main(void)  
{  
   int i=0;  
   printf("i son/pa ppid pid  fpid/n");  
   //ppid指当前进程的父进程pid  
   //pid指当前进程的pid,  
   //fpid指fork返回给当前进程的值  
   for(i=0;i<2;i++){  
       pid_t fpid=fork();  
       if(fpid==0)  
           printf("%d child  %4d %4d %4d/n",i,getppid(),getpid(),fpid);  
       else  
           printf("%d parent %4d %4d %4d/n",i,getppid(),getpid(),fpid);  
   }  
   return 0;  
}  
1
2
3
4
5
6
7
8
运行结果是：
   i son/pa ppid pid  fpid
   0 parent 2043 3224 3225
   0 child  3224 3225    0
   1 parent 2043 3224 3226
   1 parent 3224 3225 3227
   1 child     1 3227    0
   1 child     1 3226    0

这份代码比较有意思，我们来认真分析一下：
第一步：在父进程中，指令执行到for循环中，i=0，接着执行fork，fork执行完后，系统中出现两个进程，分别是p3224和p3225（后面我都用pxxxx表示进程id为xxxx的进程）。可以看到父进程p3224的父进程是p2043，子进程p3225的父进程正好是p3224。我们用一个链表来表示这个关系：
p2043->p3224->p3225
第一次fork后，p3224（父进程）的变量为i=0，fpid=3225（fork函数在父进程中返向子进程id），代码内容为：

1
2
3
4
5
6
7
8
for(i=0;i<2;i++){  
    pid_t fpid=fork();//执行完毕，i=0，fpid=3225  
    if(fpid==0)  
       printf("%d child  %4d %4d %4d/n",i,getppid(),getpid(),fpid);  
    else  
       printf("%d parent %4d %4d %4d/n",i,getppid(),getpid(),fpid);  
}  
return 0;

p3225（子进程）的变量为i=0，fpid=0（fork函数在子进程中返回0），代码内容为：

1
2
3
4
5
6
7
8
for(i=0;i<2;i++){  
    pid_t fpid=fork();//执行完毕，i=0，fpid=0  
    if(fpid==0)  
       printf("%d child  %4d %4d %4d/n",i,getppid(),getpid(),fpid);  
    else  
       printf("%d parent %4d %4d %4d/n",i,getppid(),getpid(),fpid);  
}  
return 0;

所以打印出结果：

1
2
0 parent 2043 3224 3225
0 child 3224 3225  0

第二步：假设父进程p3224先执行，当进入下一个循环时，i=1，接着执行fork，系统中又新增一个进程p3226，对于此时的父进程，p2043->p3224（当前进程）->p3226（被创建的子进程）。
对于子进程p3225，执行完第一次循环后，i=1，接着执行fork，系统中新增一个进程p3227，对于此进程，p3224->p3225（当前进程）->p3227（被创建的子进程）。从输出可以看到p3225原来是p3224的子进程，现在变成p3227的父进程。父子是相对的，这个大家应该容易理解。只要当前进程执行了fork，该进程就变成了父进程了，就打印出了parent。
所以打印出结果是：

1
2
1 parent 2043 3224 3226
1 parent 3224 3225 3227

第三步：第二步创建了两个进程p3226，p3227，这两个进程执行完printf函数后就结束了，因为这两个进程无法进入第三次循环，无法fork，该执行return 0;了，其他进程也是如此。
以下是p3226，p3227打印出的结果：

1
2
1 child   1 3227  0
1 child   1 3226  0

细心的读者可能注意到p3226，p3227的父进程难道不该是p3224和p3225吗，怎么会是1呢？这里得讲到进程的创建和死亡的过程，在p3224和p3225执行完第二个循环后，main函数就该退出了，也即进程该死亡了，因为它已经做完所有事情了。p3224和p3225死亡后，p3226，p3227就没有父进程了，这在操作系统是不被允许的，所以p3226，p3227的父进程就被置为p1了，p1是永远不会死亡的，至于为什么，这里先不介绍，留到“三、fork高阶知识”讲。

fork高阶知识

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <unistd.h>  
#include <stdio.h>  
int main(void)  
{  
   int i=0;  
   for(i=0;i<3;i++){  
       pid_t fpid=fork();  
       if(fpid==0)  
           printf("son/n");  
       else  
           printf("father/n");  
   }  
   return 0;  
  
}

它的执行结果是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
father
 son
 father
 father
 father
 father
 son
 son
 father
 son
 son
 son
 father
 son

这里就不做详细解释了，只做一个大概的分析。

1
2
3
4
5
6
7
8
9
for    i=0     1      2
     father  father   father
                  	son
             son    	father
                   	son
      son    father   father
                   	son
             son    	father
                  	son

其中每一行分别代表一个进程的运行打印结果。
总结一下规律，对于这种N次循环的情况，执行printf函数的次数为2*（1+2+4+……+2N-1）次，创建的子进程数为1+2+4+……+2N-1个。数学推理见http://202.117.3.13/wordpress/?p=81
同时，大家如果想测一下一个程序中到底创建了几个子进程，最好的方法就是调用printf函数打印该进程的pid，也即调用printf(“%d/n”,getpid());或者通过printf(“+/n”);来判断产生了几个进程。有人想通过调用printf(“+”);来统计创建了几个进程，这是不妥当的。具体原因我来分析。
老规矩，大家看一下下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <unistd.h>  
#include <stdio.h>  
int main() {  
    pid_t fpid;//fpid表示fork函数返回的值  
    //printf("fork!");  
    printf("fork!/n");  
    fpid = fork();  
    if (fpid < 0)  
        printf("error in fork!");  
    else if (fpid == 0)  
        printf("I am the child process, my process id is %d/n", getpid());  
    else  
        printf("I am the parent process, my process id is %d/n", getpid());  
    return 0;  
}

执行结果如下：
fork!
I am the parent process, my process id is 3361
I am the child process, my process id is 3362
如果把语句printf(“fork!/n”);注释掉，执行printf(“fork!”);
则新的程序的执行结果是：
fork!I am the parent process, my process id is 3298
fork!I am the child process, my process id is 3299
程序的唯一的区别就在于一个/n回车符号，为什么结果会相差这么大呢？
这就跟printf的缓冲机制有关了，printf某些内容时，操作系统仅仅是把该内容放到了stdout的缓冲队列里了,并没有实际的写到屏幕上。但是,只要看到有/n 则会立即刷新stdout,因此就马上能够打印了。
运行了printf(“fork!”)后,“fork!”仅仅被放到了缓冲里,程序运行到fork时缓冲里面的“fork!” 被子进程复制过去了。因此在子进程度stdout缓冲里面就也有了fork! 。所以,你最终看到的会是fork! 被printf了2次！！！！
而运行printf(“fork! /n”)后,“fork!”被立即打印到了屏幕上,之后fork到的子进程里的stdout缓冲里不会有fork! 内容。因此你看到的结果会是fork! 被printf了1次！！！！
所以说printf(“+”);不能正确地反应进程的数量。
大家看了这么多可能有点疲倦吧，不过我还得贴最后一份代码来进一步分析fork函数。

信号量

linux的信号量机制

对于与信号量操作有关的接口，Linux下主要提供了以下几个函数，值得注意的是，在Linux下的C接口中，这些函数的操作对象都是信号量值组，也就是一个信号量值的链表

在Linux系统中，使用信号量通常分为以下4个步骤：

① 创建信号量或获得在系统中已存在的信号量，此时需要调用 semget() 函数。不同进程通过使用同一个信号量键值来获得同一个信号量。

② 初始化信号量，此时使用 semctl() 函数的SETVAL操作。当使用二维信号量时，通常将信号量初始化为1。

③ 进行信号量的PV操作，此时，调用 semop()函数。这一步是实现进程间的同步和互斥的核心工作部分。

④ 如果不需要信号量，则从系统中删除它，此时使用semctl()函数的 IPC_RMID操作。需要注意的是，在程序中不应该出现对已经被删除的信号量的操作。

1、semget()函数

它的作用是创建一个新信号量或取得一个已有信号量，原型为：

1
int semget(key_t key, int num_sems, int sem_flags);

第一个参数key是整数值（唯一非零），不相关的进程可以通过它访问一个信号量，它代表程序可能要使用的某个资源，程序对所有信号量的访问都是间接的，程序先通过调用semget()函数并提供一个键，再由系统生成一个相应的信号标识符（semget()函数的返回值），只有semget()函数才直接使用信号量键，所有其他的信号量函数使用由semget()函数返回的信号量标识符。如果多个程序使用相同的key值，key将负责协调工作。

第二个参数num_sems指定需要的信号量数目，它的值几乎总是1。

第三个参数sem_flags是一组标志，当想要当信号量不存在时创建一个新的信号量，可以和值IPC_CREAT做按位或操作。设置了IPC_CREAT标志后，即使给出的键是一个已有信号量的键，也不会产生错误。而IPC_CREAT | IPC_EXCL则可以创建一个新的，唯一的信号量，如果信号量已存在，返回一个错误。

semget()函数成功返回一个相应信号标识符（非零），失败返回-1.

2、semop()函数

它的作用是改变信号量的值，原型为：

1
int semop(int sem_id, struct sembuf *sops, size_t num_sem_ops);

sem_id是由semget()返回的信号量标识符。

sops是指向信号量操作数组。

sembuf结构的定义如下：

1
2
3
4
5
6
7
struct sembuf{
    short sem_num; // 除非使用一组信号量，否则它为0,多组信号量中表示信号量在组内的索引值
    short sem_op;  // 信号量在一次操作中需要改变的数据，通常是两个数，一个是-1，即P（等待）操作，
                   // 一个是+1，即V（发送信号）操作。
    short sem_flg; // 通常为SEM_UNDO,使操作系统跟踪信号，
                   // 并在进程没有释放该信号量而终止时，操作系统释放信号量
};

sem_flg 参数：

该参数可设置为 IPC_NOWAIT 或 SEM_UNDO 两种状态。只有将 sem_flg 指定为 SEM_UNDO 标志后，semadj （所指定信号量针对调用进程的调整值）才会更新。 此外，如果此操作指定SEM_UNDO，系统更新过程中会撤消此信号灯的计数（semadj）。此操作可以随时进行—它永远不会强制等待的过程。调用进程必须有改变信号量集的权限。
sem_flg公认的标志是 IPC_NOWAIT 和 SEM_UNDO。如果操作指定SEM_UNDO，当该进程终止时它将会自动撤消。

num_sem_ops表示的是操作数组sops中的操作个数，通常取值1。

semop函数成功返回信号量标识符，失败返回-1。

该函数所做的对于信号量的操作都是原子操作，即整个行为是一个整体，是不可打断的。所有操作是否可以立即执行取决于在个人sem_flg领域的IPC_NOWAIT标志的存在。

semop函数操作中的sem_op（+1或者-1）是基于semctl函数对信号量初始化的值的基础上的。例如semctl函数将信号量初始化为100，sem_op(+1)就是100+1。由此看出信号量初始化是很有必要的。

3、semctl()函数

该函数用来直接控制信号量信息，它的原型为：

1
int semctl(int sem_id, int sem_num, int command, ...);

函数的第一个参数 semid 为信号量集的标识符；
函数的第二个参数sem_num则是表示即将要进行操作的信号量的编号，即信号量集合的索引值，其中第一个信号量的索引值为0。

函数的第3个参数command代表将要在集合上执行的命令，其取值含义如下，通常用特定的宏代替：

IPC_STAT:获取某个信号量集合的semid_ds结构，并将其储存在semun联合体的buf参数所指的地址之中

IPC_SET:设置某个集合的semid_ds结构的ipc_perm成员的值，该命令所取的值是从semun联合体的buf参数中取到的

IPC_RMID:从内核删除该信号量集合

GETALL:用于获取集合中所有信号量的值，整数值存放在无符号短整数的一个数组中，该数组有联合体的array成员所指定

GETNCNT:返回当前正在等待资源的进程的数目

GETPID:返回最后一次执行PV操作（semop函数调用）的进程的PID

GETVAL:返回集合中某个信号量的值

GETZCNT:返回正在等待资源利用率达到百分之百的进程的数目

SETALL:把集合中所有信号量的值，设置为联合体的array成员所包含的对应值

SETVAL:将集合中单个信号量的值设置为联合体的val成员的值

command通常是下面两个值中的其中一个

SETVAL：用来把信号量初始化为一个已知的值。ps :这个值通过union semun中的val成员设置，其作用是在信号量第一次使用前对它进行设置。

IPC_RMID：用于删除一个已经无需继续使用的信号量标识符。

对于该函数，只有当command取某些特定的值的时候，才会使用到第4个参数，第4个参数它通常是一个union semum结构，定义如下：

1
2
3
4
5
union semun{    
    int val;    
    struct semid_ds *buf;    
    unsigned short *arry;    
};

对于第4个参数arg，
当执行SETVAL命令时用到这个成员，他用于指定要把信号量设置成什么值，涉及成员：val

在命令IPC_STAT/IPC_SET中使用，它代表内核中所使用内部信号量数据结构的一个复制 ，涉及成员：buf

在命令GETALL/SETALL命令中使用时，他代表指向整数值一个数组的指针，在设置或获取集合中所有信号量的值的过程中，将会用到该数组，涉及成员：array

例子：

github上的OS2例题。

共享内存

参考下文：

https://blog.csdn.net/guoping16/article/details/6584043

发表于 更新于 分类于 ，

补充点

引用（&）

&在C语言表示的是取地址符————用在函数传参中的指针赋值

在C++语言中引用是某一个变量的别名，对引用的操作与对变量直接操作完全一样。

1
2
int a;
int &ra=a;//定义引用ra,它是变量a的引用，即别名
  • &在此不是求地址运算，而是起标识作用。
  • 声明引用时，必须同时对其进行初始化。
  • 类型标识符是指目标变量的类型。
  • 引用声明完毕后，相当于目标变量名有两个名称————目标原名和引用名，且不能再把该引用名作为其他变量名的别名
  • 引用本身不占存储单元，本身不是一种数据类型
  • 不能建立数组的引用

引用的作用

  • 作为函数的参数，效果是和传递指针的效果是一样的
  • 使用引用传递函数的参数，由于在内存中没有产生实参的副本，它是直接对实参操作。

常引用

1
2
3
4
5
常引用声明方式：const 类型标识符 &引用名=目标变量名；
int a ;
const int &ra=a;
ra=1; //错误
a=1; //正确

不能通过引用对目标变量的值进行修改，从而使引用的目标成为const

引用作为返回值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream.h>
float temp; //定义全局变量temp
float fn1(float r); //声明函数fn1
float &fn2(float r); //声明函数fn2
float fn1(float r) //定义函数fn1，它以返回值的方法返回函数值
{
　temp=(float)(r*r*3.14);
　return temp;
}
float &fn2(float r) //定义函数fn2，它以引用方式返回函数值
{
　temp=(float)(r*r*3.14);
　return temp;
}
void main() //主函数
{
　float a=fn1(10.0); //第1种情况，系统生成要返回值的副本（即临时变量）
　float &b=fn1(10.0); //第2种情况，可能会出错（不同 C++系统有不同规定）
　//不能从被调函数中返回一个临时变量或局部变量的引用
　float c=fn2(10.0); //第3种情况，系统不生成返回值的副本
　//可以从被调函数中返回一个全局变量的引用
　float &d=fn2(10.0); //第4种情况，系统不生成返回值的副本
　//可以从被调函数中返回一个全局变量的引用
　cout<<a<<c<<d;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream.h>
int &put(int n);
int vals[10];
int error=-1;
void main()
{
put(0)=10; //以put(0)函数值作为左值，等价于vals[0]=10;
put(9)=20; //以put(9)函数值作为左值，等价于vals[9]=20;
cout<<vals[0];
cout<<vals[9];
}
int &put(int n)
{
if (n>=0 && n<=9 ) return vals[n];
else { cout<<"subscript error"; return error; }
}

引用和多态

1
2
3
4
class 　A;
class 　B：public A{……};
B 　b;
A 　&Ref = b; // 用派生类对象初始化基类对象的引用

Ref 只能用来访问派生类对象中从基类继承下来的成员，是基类引用指向派生类。如果A类中定义有虚函数，并且在B类中重写了这个虚函数，就可以通过Ref产生多态效果。

虚函数

抽象类是指包括至少一个纯虚函数的类。

C++允许用户使用虚函数 (virtual function) 来完成 运行时决议 这一操作，这与一般的 编译时决定 有着本质的区别

  • 在基类用virtual声明成员函数为虚函数。这样就可以在派生类中重新定义此函数，为它赋予新的功能，并能方便被调用。
    • 在派生类中重新定义此函数，要求函数名，函数类型，函数参数个数和类型全部与基类的虚函数相同，并根据派生类的需要重新定义函数体。
  • 在类外定义虚函数时，不必在定义virtual
  • c++规定，当一个成员函数被声明为虚函数后，其派生类的同名函数都自动成为虚函数。因此在派生类重新声明该虚函数时，可以加virtual，也可以不加，但习惯上一般在每层声明该函数时都加上virtual，使程序更加清晰。
  • 如果再派生类中没有对基类的虚函数重新定义，则派生类简单的继承起基类的虚函数。

实现机制

用虚表和虚指针

是每个类用了一个虚表，每个类的对象用了一个虚指针。虚表是和类对应的，虚表指针是和对象对应的。

虚表

  • 一个类的虚函数的地址表，这张表解决了继承、覆盖的问题，保证其容真实反应实际的函数

  • 没有覆盖父类的虚函数是毫无意义的。

多态

C++中的虚函数的作用主要是实现了多态的机制。

多态用虚函数来实现，结合动态绑定，此时的调用就不会在编译时候确定而是在运行时确定。不在单独考虑指针/引用的类型而是看指针/引用的对象的类型来判断函数的调用，根据对象中虚指针指向的虚表中的函数的地址来确定调用哪个函数

虚函数是在基类中定义的，目的是不确定它的派生类的具体行为。故可以理解成java的父类中待覆写的函数

混淆点

关于函数的调用机制

（1）调用过程：建立函数调用栈—保存调用函数的运行状态和返回地址—传参—进入被调函数。

（2）传参机制：传参不一定会压栈！fastcall(快调)一般会由寄存器传参，另外当参数不超过4个时一般也由寄存器传参，否则会压栈。压栈顺序一般是从右到左

传参方式

值传递（传副本）

形参只是实参的拷贝

在函数结束时，形参作为局部变量会被释放，对实参不会产生任何影响。若为类的对象会调用拷贝构造，这种深拷贝操作会影响到传参效率。（可理解为“单向接口”）

指针传递

指针本质上是一个变量，该变量的值是一个地址，指针在逻辑上是独立的，可以被改变。

传递的是实参的地址，所以函数内部对形参得操作会“同步更新”到实参。（可理解为“双向接口”）

引用传递

传递的是实参的别名，传参时形参被绑定到实参对象上，因此函数内部对形参的操作也都会“同步更新”到源实参。（可理解为“双向接口”）

引用传递和值传递的异同

相同点

  • 都是地址的概念

不同点

  • 指针是一个实体（替身）；引用只是一个别名（本体的另一个名字）

  • 引用只能在定义时被初始化一次，之后不可改变，即“从一而终”；指针可以修改，即“见异思迁”；

  • 引用不能为空（有本体，才有别名）；指针可以为空；

  • sizeof 引用，得到的是所指向变量的大小；sizeof 指针，得到的是指针的大小；

  • 指针 ++，是指指针的地址自增；引用++是指所指变量自增；

  • 引用是类型安全的，引用过程会进行类型检查；指针不会进行安全检查；

关于static用法

静态局部变量！=全局变量，二者生命周期相同，但作用域不同，静态局部变量只对函数体内部可见。

static修饰全局变量：限定该变量只在该文件中可用。

static修饰外部函数：往往在函数声明中加static修饰，限定该函数只在该文件可用（若在头文件中声明，则限定只在其对应的源文件中可用）

类中static修饰的成员。静态成员与类的对象实体无关，是该类的共享变量。

关于extern用法

C/C++头文件中的函数声明默认为extern，即外部可用（其他源文件只需包含头文件即可使用）。和static修饰的效果相反。

带extern的变量仅仅是声明而不是定义！用extern使变量可以在多文件中共享，主要有两种做法：

  • 在源文件中定义，其他需要使用该变量的源文件用extern声明。（表示该变量在其它文件中定义，即一次定义，多次extern声明）
  • 在源文件中定义，其对应的头文件中extern声明，其他需要使用该变量的源文件包含该头文件即可。（更加标准的做法）

内联

用途：定义或声明函数时返回值前加上inline修饰能避免函数调用带来的时间和空间开销，提高效率，适用于反复执行的核心代码。内部实现机制其实是编译时按函数体展开代码，避免了函数调用的一系列压栈出栈过程。

限制：

​ （1）不能出现复杂的控制结构语句；

​ （2）递归函数不能用作内联函数；

​ （3）内联函数体不宜代码过长，只适合数行的小函数。

注：1.内联和宏定义均属于代码替换机制，但前者安全性更好，宏只是预处理做简单的符号替换而不会做类型检查。内联可以完全替代宏，反之不能。

​ 2.inline关键字只是一种“建议”，是否采用内联机制取决于编译器。

重载

用途：C++特有机制。让同一种算法针对不同类型使用相同的函数名，提高代码可读性，重载的函数至少在参数个数或类型上有所区别，仅返回值区别不能重载！

1
2
void func(int);和int func(int);//编译器无法区分
int abs(int);和double abs(double);//C++通过名字粉碎技术自动匹配

ps:重写是面向对象中子类对父类虚函数的重新实现

底层const修饰的参数以及常量成员函数也可以重载。

友元

  • 友元(frend)机制允许一个类将对其非公有成员的访问权授予指定的函数或者类
  • 友元的声明以friend开始，它只能出现在类定义的内部

友元函数

友元函数是一个不属于类成员的函数，但它可以访问该类的私有成员。————友元函数视作好像是该类的一个成员

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>

using namespace std;

class A
{
public:
    friend void set_show(int x, A &a);      //该函数是友元函数的声明
private:
    int data;
};

void set_show(int x, A &a)  //友元函数定义，为了访问类A中的成员
{
    a.data = x;
    cout << a.data << endl;
}
int main(void)
{
    class A a;

    set_show(1, a);

    return 0;
}

友元类

友元类的所有成员函数都是另一个类的友元函数，都可以访问另一个类中的隐藏信息（包括私有成员和保护成员）。

关于友元类的注意事项：

(1) 友元关系不能被继承。
(2) 友元关系是单向的，不具有交换性。若类B是类A的友元，类A不一定是类B的友元，要看在类中是否有相应的声明。
(3) 友元关系不具有传递性。若类B是类A的友元，类C是B的友元，类C不一定是类A的友元，同样要看类中是否有相应的申明。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>

using namespace std;

class A
{
public:
    friend class C;                         //这是友元类的声明
private:
    int data;
};

class C             //友元类定义，为了访问类A中的成员
{
public:
    void set_show(int x, A &a) { a.data = x; cout<<a.data<<endl;}
};

int main(void)
{
    class A a;
    class C c;

    c.set_show(1, a);

    return 0;
}

友元成员函数

使类B中的成员函数成为类A的友元函数，这样类B的该成员函数就可以访问类A的所有成员了。

vector用法

vector 是向量类型，它可以容纳许多类型的数据，如若干个整数，所以称其为容器。

vector是一个类模板，而不是类型。

动态联编与静态联编

c++一般的子类和父类继承关系的时候，都是使用的是静态联编（和之前学习的指针的用法一致）参考：https://blog.csdn.net/neiloid/article/details/6934129

参考：https://blog.csdn.net/neiloid/article/details/6934129

参考：https://blog.csdn.net/gaoxin1076/article/details/8298279

联编是指一个计算机程序自身彼此关联的过程,在这个联编过程中,需要确定程序中的操作调用(函数调用)与执行该操作(函数)的代码段之间的映射关系;按照联编所进行的阶段不同,可分为静态联编和动态联编;

仔细读读红色字体的那部分句子。我们就能很清楚的明白什么是联编了。给大家举个最通俗易懂的例子好了：

A类中有fun这个函数， B类中也有fun这个函数，现在我在类外的main函数里面调用fun 函数。

那么main函数就是函数调用，调用fun函数，

而A类中的fun函数和B类中的fun函数就是执行该操作的代码段

所以现在联编就是实现两者的映射关系。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class A
{	
	void func() {cout<<"It's A"<<endl;

};

class B
{	
	void func() {cout<<"It's B"<<endl;

};
int main()
{
	func();
}

联编就是决定将main函数中的func（）的函数调用映射到A中的func函数还是B中的func函数的过程。

2.静态联编 和 动态联编 的定义

知道了什么事联编，那么再来理解动态联编 和静态联编也就不难了

静态联编:
是指联编工作是在程序编译连接阶段进行的,这种联编又称为早期联编;因为这种联编是在程序开始运行之前完成的;
在程序编译阶段进行的这种联编又称静态束定;在编译时就解决了程序中的操作调用与执行该操作代码间的关系,确定这种关系又被称为束定;编译时束定又称为静态束定;

拿上面的例子来说，静态联编就是在编译的时候就决定了main函数中调用的是A中的func还是B中的func。一旦编译完成，那么他们的映射关系就唯一确定了。

动态联编:
编译程序在编译阶段并不能确切地知道将要调用的函数,只有在程序执行时才能确定将要调用的函数,为此要确切地知道将要调用的函数,要求联编工作在程序运行时进行,这种在程序运行时进行的联编工作被称为动态联编,或动态束定,又叫晚期联编;C++规定:动态联编是在虚函数的支持下实现的;

动态联编在编译的时候还是不知道到底应该选择哪个func函数，只有在真正执行的时候，它才确定。

静态联编和动态联编都是属于多态性的,它们是在不同的阶段进对不同的实现进行不同的选择;

也可以这么说：C++多态有两种形式，动态多态和静态多态（函数重载）；动态多态是指一般的多态，是通过类继承和虚函数机制实现的多态；静态多态是通过模板来实现，因为这种多态实在编译时而非运行时，所以称为静态多态。

3.静态联编

首先还是拿个例子来说事吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include <iostream>
using namespace std;
class shape{
  public:
    void draw(){cout<<"I am shape"<<endl;}
    void fun(){draw();}
};
class circle:public shape{
  public:
    void draw(){cout<<"I am circle"<<endl;}
};
void main(){
    circle  oneshape;
    oneshape.fun();
}

现在我们详细具体定义了一开始的A类和B类以及func函数。让我们来分析一下：
调用oneshape.fun()的时候，进入类shape中的fun函数。

现在我们的问题就是：fun函数调用的draw到底是shape里面的draw还是circle中的draw？？

答案是：它调用了cshape这个基类的draw函数。所以输出了 I am shape

那么一直困扰我的问题是：为什么调用基类的draw而不是派生类中得draw呢？

书上好像没有具体讲，上课的时候老师那也根本不会讲。

自己想了一下，应该可以从汇编的角度理解：

1.调用oneshape.fun()，这里是一个跳转指令，进入类shape中的fun函数所在的代码段

2.类shape的代码段是依次顺序放置的。进入fun函数后，现在我们要调用draw的地址。

由于没有另外的数据结构来保存draw的地址，所以程序所知道的，必然只有在shape类中的draw地址了，仅仅用一个跳转指令

在我的vs2010的反汇编调试窗口下是这样的一句代码：

013B1546 call shape::draw (13B10F5h)

很明确这里指出了shape::draw，也就确定了映射关系，完成了联编。

C++和java的异同

  1. Java源码会先经过一次编译，成为中间码，中间码再被解释器解释成机器码。对于Java而言，中间码就是字节码(.class)，而解释器在JVM中内置了。

    C++源码一次编译，直接在编译的过程中链接了，形成了机器码。

  2. Java是纯面向对象的语言，所有代码（包括函数、变量）都必须在类中定义。而C++中还有面向过程的东西，比如是全局变量和全局函数。

  3. C++支持多继承，Java中类都是单继承的。但是继承都有传递性，同时Java中的接口是多继承，类对接口的实现也是多实现。

变量和类型

  • Java没有无符号整数。（无符号右移在Java中强制用三个右尖括号表示）。

  • Java有内置类型String，而C++没有。C++的std::string是可变的，类似于Java的StringBuffer。

  • Java中不存在指针。Java的引用是功能弱化的指针，只能做“调用所指对象的方法”的操作。

  • Java中，对象只能由引用传递，C＋＋中对象可由值或引用传递。

类机制

  • Java是完全面向对象的，所有方法都必须写在类中。

C++标准库

IO库