rhb_blog

rao的博客

0%

编译原理-静态语义分析和中间代码生成

发表于 更新于 分类于 ，

符号表

符号表的作用

  • 用来存放有关标识符（符号）的属性信息

    • 这些信息会在编译的不同阶段用到
    • 符号表的内容将用于静态语义检查和产生中间代码
    • 在目标代码生成阶段，符号表是对符号名进行地址分配的依据
    • 对一个多遍扫描的编译程序，不同遍所用的符号表也会有所不同，因为每遍所关心的信息或所能得到的信息会有差异

  • 用来体现作用域与可见性信息

符号的常见属性

① 符号名

② 符号的类型：常量、变量、过程/函数、类的名称等

③ 符号的存储类别：常量、变量的数据类型，过程函数的返回类型等【决定了其存储格式和允许的操作】

④ 符号的作用域及可视性

⑤ 符号变量的存储类别和存储分配信息
存储类别确定其分配的区域，静态或动态数据区，堆区或栈区，存储分配信息如单元的大小，相对于某个存储区域的偏移位置等等

⑥ 符号的其它属性

  • 数组内情向量
  • 记录结构的成员信息
  • 函数及过程的形参

符号表的实现

针对符号表的常见操作

  • 创建符号表：在编译开始，或进入一个作用域
  • 插入表项：在遇到新的标识符声明时进行
  • 查询表项：在引用标识符时进行
  • 修改表项：在获得新的语义值信息时进行
  • 删除表项：在标识符成为不可见或不再需要它的任何信息时进行
  • 释放符号表空间：在编译结束前或退出一个作用域

实现符号表的常用数据结构

  • 一般的线性表
    如：数组，链表，等
  • 有序表
    查询较无序表快，如可以采用折半查找
  • 二叉搜索树
  • Hash表

作用域与符号表组织

  • 所有作用域共用一个全局符号表

  • 每个作用域都有各自的符号表

作用域与可见性

  • 嵌套的作用域（nested scopes）

  • 开作用域与闭作用域（相应于程序中特殊点）

    • 该点所在的作用域为当前作用域
    • 当前作用域与包含它的程序单元所构成的作用域称为开作用域（open scopes）,即嵌套重叠的作用域
    • 不属于开作用域的作用域称为闭作用域（close scopes）

  • 常用的可见性规则（visibility rules）

    • 在程序的任何一点，只有在该点的开作用域中声明的名字才是可访问的
    • 若一个名字在多个开作用域中被声明，则把离该名字的某个引用最近的声明作为该引用的解释
    • 新的声明只能出现在当前作用域

作用域与符号表组织

  • 作用域与多符号表组织
    • 每个作用域都有各自的符号表
    • 维护一个符号表的作用域栈，每个开作用域对应栈中的一个入口，当前的开作用域出现在该栈的栈顶
    • 当一个新的作用域开放时，新符号表将被创建，并将其入栈
    • 在当前作用域成为闭作用域时，从栈顶弹出相应的符号表

静态语义分析

静态语义： 刻画程序在静态一致性或完整性方面的特征；仅当程序通过了静态语义检查，才能完成后续的中间代码生成和目标代码优化。

动态语义： 刻画程序执行时的行为。比如除数为0，数组越界等错误，需要生成相应代码

主要任务

  • 类型检查（type checks）
    检查每个操作是否遵守语言类型系统的定义

  • 名字的作用域（scope）分析
    建立名字的定义和使用之间联系

  • 控制流检查（flow-of-control checks）
    控制流语句必须使控制转移到合法的地方（如break语句必须有合法的语句包围它）

  • 唯一性检查（uniqueness checks）
    很多场合要求对象只能被定义一次（如枚举类型的元素不能重复出现）

  • 名字的上下文相关性检查（name-related checks）
    某些名字的多次出现之间应该满足一定的上下文相关性

类型检查

类型检查程序（type checker）：负责类型检查

  • 验证程序的结构是否匹配上下文所期望的类型
  • 为相关阶段搜集及建立必要的类型信息
  • 实现某个类型系统（type system）

中间代码生成

源程序的不同表示形式,也称为中间表示。其作用：

  • 源语言和目标语言之间的桥梁，避开二者之间较大的语义跨度，使编译程序的逻辑结构更加简单明确
  • 有利于编译程序的重定向
  • 有利于进行与目标机无关的优化

常见的中间表示的形式

有不同层次不同目的之分。常见中间表示形式：

  • AST（Abstract syntax tree，抽象语法树）
    DAG（Directed Acyclic Graph,有向无圈图，通过优化技术得到改进型 AST）
  • TAC（Three-address code,三地址码，四元式）
  • P-code （特别用于 Pasal 语言实现）
  • Bytecode（Java 编译器的输出, Java 虚拟机的输入）
  • SSA（Static single assignment form，静态单赋值形式）【静态单赋值形式，程序中的名字只有一次赋值。】

生成抽象语法树

(1) 树的根节点是开始符

(2) 所有的内节点都是非终结符

(3) 所有的叶子节点都是终结符

生成三地址码

通过遍历语法树或在归约时，生成三地址码，后续要用到的四元式：

• 赋值语句 x := y op z （op 代表二元算术/逻辑运算）

• 赋值语句 x := op y （op 代表一元运算）

• 复写语句 x := y （y 的值赋值给 x）

• 无条件跳转语句 goto L （无条件跳转至标号 L）

• 条件跳转语句 if x rop y goto L （rop 代表关系运算）

• 标号语句 L : （定义标号 L）

• 过程调用语句序列 param x1 … param xn call p,n

• 过程返回语句 return y （y 可选，存放返回值）

• 下标赋值语句 x := y[i] 和 x[i] := y （前者表示将地址 y 起第i个存储单元的值赋给 x，后者类似）

• 指针赋值语句 x := *y 和 *x := y

赋值语句及算术表达式的语法制导翻译

中间代码（中间语言）

中间代码也叫中间语言（Intermediate code /language）是：源程序的一种内部表示，不依赖目标机的结构。介于源语言和目标语言的中间语言形式。

中间代码的特点：

1、独立于机器

2、复杂性界于源语言和目标语言之间

中间代码的优点

1、使得编译程序的逻辑结构清楚；

2、利于不同目标机上实现同一种语言；

3、利于进行与机器无关的优化；

中间语言将编译程序分为前端和后端有利于编译程序的移植。例如：保持编译程序的前端不变，替换其后端，就可以将原来的某个语言的编译程序改造成同一个语言，不同目标机器的程序。如果保持后端不变，替换前端，就可以将某个机器上的某个语言的编译程序改造成同一个机器上的另一个语言的编译程序。

常用的中间语言

  • 后缀式：逆波兰表示
  • 图表示：抽象语法树AST、有向无环图DAG
  • 三地址代码：
    • 三元式
    • 四元式
    • 间接三元式

后缀式

逆波兰表示法即为后缀表示法，而默认我们使用的表达式是中缀表示法

程序设计语言中的表示 —–逆波兰表示—–
a+ba+b ab+ab+
−a−a a@a@
a+b∗ca+b∗c abc∗+abc∗+
(a+b)∗c(a+b)∗c ab+c∗ab+c∗
a:=b∗c+b∗da:=b∗c+b∗d abc∗bd∗+:=abc∗bd∗+:=
a:=b∗(c+b)∗(−d)a:=b∗(c+b)∗(−d) bcb+∗d@∗:=

逆波兰式的使用：需使用额外的标识符栈。顺序扫描逆波兰表达式的时候，遇到标识符直接入栈。

遇到运算符时：

  1. 根据运算符目数，从栈顶取出相应数目的标识符做运算，并把运算结果压栈
  2. 运算结束时，标识符栈应该只剩下一个元素，且为运算结果

图表示法

抽象语法树和有向无环图

抽象语法树

在语法树中去掉一些对翻译不必要的信息后，获得的更有效的源程序的中间表示，这种经过变换后的语法树称为抽象语法树。

在抽象语法树中，操作符和关键字都不作为叶子节点出现，而是把它们作为内部节点，即这些叶子节点的父节点。

有向无环图

对表达式中的每个子表达式，DAG都有一个结点，一个内部结点代表一个操作符，他的孩子代表操作数。

在一个DAG中代表公共子表达式的节点具有多个父结点（与抽象语法树中公共子表达式被表示为重复的子树不同）

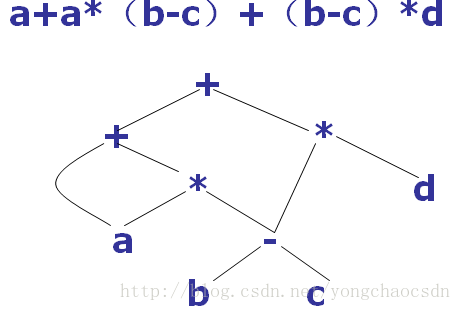
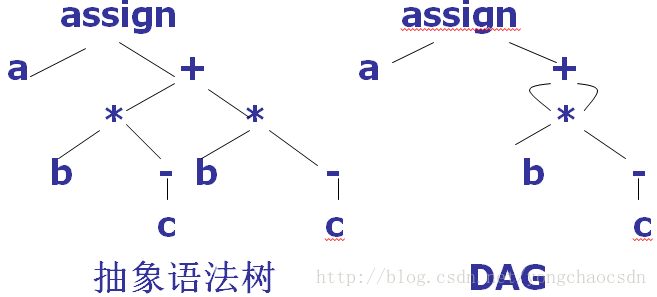
树形表示

树形表示和三元式表示非常相似，如a:=b∗c+b∗d表示为：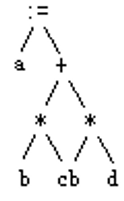
img
注意赋值表达式中被赋值对象在树的左孩子节点位置

单目运算−T1直接表示成：

img

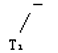
三地址代码表示

三地址代码可以看作是抽象语法树或有向无环图的一种线性表示

三地址代码最基本的用法形式:

x:=y op z

​ 其中x、y、z为名字、常数或编译时产生的临时变量；op代表运算符号。每个语句的右边只能有一个运算符。

三地址代码可以看成是抽象语法树一种线性表示

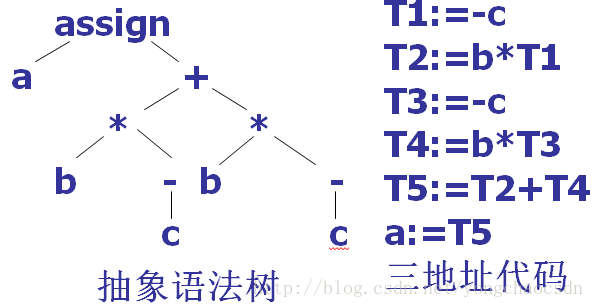
三地址代码可以看成是DAG的一种线性表示

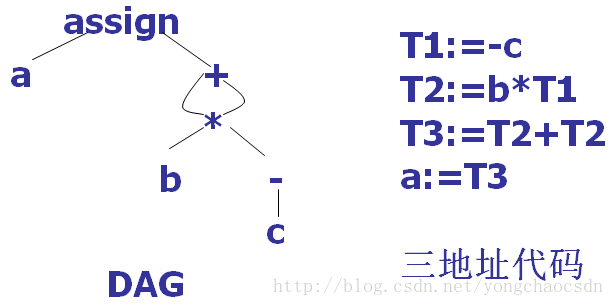
三地址码的各种形式：

1
2
3
4
5
6
7
1.x:=yop z          x := op z                         x:=y
2.Goto L             ifx relopy gotoL         if a goto L
3【传参、转子】.Param x         call p,n                           
4【返回语句】.return y
5【索引赋值】.x:=y[i]             x[i]:=y
6【地址和指针赋值】.x:=&y            x:=*y                  *x:=y     
赋值语句翻译为三地址码的属性文法

三元式

三元式$(op,A_1,A_2)$

op为运算符
A1为第一运算对象
A2为第二运算对象

例如$a:=b∗c+b∗d$表示为：
$(1)(∗,b,c)\
(2)(∗,b,d)\
(3)(+,(1),(2)) 这里用(1)和(2)来表示中间计算结果的显式引用\
(4)(:=,(3),a)( 这里相当于a:=(3)$

而单目运算的−b可以表示成(−,b,/)

四元式

四元式实际上是一种“三地址语句”的等价表示，是一个带有四个域的记录结构。

四元式$(op,A_1,A_2,R)$

op为运算符
A1为第一运算对象
A2为第二运算对象
R为运算结果

例如$a:=b∗c+b∗d$的四元式表示：
$(1)(∗,b,c,t_1)\
(2)(∗,b,d,t_2)\
(3)(+,t_1,t_2,t_3)\
(4)(:=,t_3,−,a)$

和三元式的差别在于，四元式对中间结果的引用必须通过给定的名字(临时变量)

它的三地址码写法为：
$t_1:=b∗c\
t_2:=b∗d\
t_3:=t_1∗t_2\a:=t_3$

三元式和四元式的比较

相同点：

1、无论在一个三元式序列还是四元式序列中，各个三元式或四元式都是按相应表达式的实际运算顺序出现的；

2、对同一表达式而言，所需的三元式或四元式的个数一般都是相同的。

不同点：

1、由于三元式没有result字段，且不需要临时变量，故三元式比四元式占用的存储空间少；

2、在进行代码优化处理时，常常需要挪动一些运算的位置，这对于三元式序列来说是很困难的，但对于四元式来说，由于四元式之间的相互联系是通过临时变量来实现的，所以，更改其中一些四元式给整个系列带来的影响就比较小。

三地址代码-间接三元式

建立两个与三元式有关的表格，一个称为三元式表，用于存放各三元式本身；另一个称为执行表，它按照三元式的执行顺序，依次列出相应各三元式在三元式表中的位置，也就是说我们用一个三元式表连同执行表来表示中间代码。通常我们称这种表示方法为间接三元式。

三元式

$x：=（a+b）c\
b：=a+b\
y：=c（a+b$

（1）（+，a，b） （5） （+，a，b）
（2）（ *，（1），c） （6）（ *，c，（5））
（3）（：=，x，（2）） （7）（：=，y，（6））
（4）（：=，b，（1））

间接三元式

执行表 三元式表

（1） （1）（+，a，b）
（2） （2）（*，（1），c）
（3） （3）（：=，x，（2））
（4） （4）（：=，b，（1））
（1） （5）（：=，y，（2））
（2）
（5）

三元式与间接三元式之间的区别

1、由于间接三元式在执行表中已经依次列出每次要执行的那个三元式，若其中有相同的三元式，则仅需在三元式表中保存其中之一，即三元式的项数一般比执行表的项数少；

2、当进行代码优化需要挪动运算顺序时，则只需对执行表进行相应地调整，而不必再改动三元式本身，这样，就避免了前面讲到的因改变三元式的顺序所引起的麻烦。

赋值语句的翻译

布尔表达式的翻译

布尔表达式在程序设计语言中有两个作用：

  1. 计算逻辑值
  2. 用于改变控制流语句中的条件表达式

控制流语句包含循环、分支两大类。

通常我们只考虑如下文法生成的布尔表达式：
$E→EandE∣EorE∣notE∣idropid∣id∣true∣falseE→EandE∣EorE∣notE∣idropid∣id∣true∣false$
其中$rop$是关系符，如$<=,<,=,>,>=<=,<,=,>,>=$等
布尔运算符的优先顺序为$not>and>ornot>and>or$
并且$and$和$not$服从左结合

布尔表达式的计算有两种方法：

  1. 计算各部分的真假值，最后计算出整个表达式的值
    $(1and0)and(0or1)=0and1=0$
  2. 短路法：AandB如果A=0则直接得到0；AorB如果A=1则直接得到1。这种方式若B为一个带返回值的过程调用会引发副作用

布尔表达式翻译成四元式序列，如a or b and not c的翻译结果为：
(1)t1:=not c
(2)t2:=b and t1
(3)t3:=a or t2

条件语句中布尔表达式的翻译

现在有文法：
S→if E then S1∣if E then S1 else S2∣while E do S1

翻译这部分的题目主要是以给定四元式序列，然后填空。

对布尔表达式E=a rop b，可以翻译成：
(1)if a rop b goto E.true
(2)goto E.false

但此时E.true和E.false的值仍不能被确定。例如：
S→if E then S1 else S2

E.true的值为S1的第一条四元式的地址
E.false的值为S2的第一条四元式的地址

例如：

1
2
3
4
5
6
7
8
9
10
//假设要翻译 if a<b or c<d and e>f ...这段程序

//理想的情况是翻译成下面这样
（1）　if a＜b goto E.true //E.true代表该if...else...逻辑的正向逻辑段入口地址，但是翻译当前bool表达式显然是暂且还不能确定E.true的
（2）　goto （3）
（3）　if c＜d　goto （5）
（4）　goto E．false       //E.false代表if...else...的反向逻辑段入口地址
（5）　is e＞f goto E．true
（6）　goto E．false //到bool表达式翻译完成时，才能确定原来逻辑块的正向段入口地址是7
（7） ...

可以看到上面的出现E.true和E.false的地方是需要回填的逻辑地址，这里比较常见的思路可能是额外为每个逻辑地址保存一个数组用来记录需要的所有地址，比如定义一个E.true-speicific-array并将(1）（2）填入该数组中。这种做法显然是很笨的，有没有比较好的方法？这便是”拉链“式解决方案，借鉴自链表的思想，为所有需要回填E.true的指令行首尾串在一起。

……
(p−1)…S1 end
(p) goto q
(p+1) S2 begin…
……
(q−1)… S2 end
(q)…

在产生出S1和S2的状态块后，才能进行地址回填。上面的E.true应填(7)，而E.false应填(p+1)。

为了解决地址回填的问题，需要采用拉链法，把需要回填E.true的所有四元式构造并维护一条真链的链表，把需要回填E.false的所有四元式构造一条假链的链表

对于上面的例子，真链和假链如下图：

img

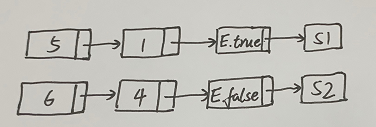
其中(5)为真链的链首，(6)为假链的链首。一旦确定S1和S2的地址，就可以沿着链作地址回填

但还有3种情况会使得四元式序列变得十分复杂，这里不讨论：

  1. 连续的or或连续的and
  2. 连续的if−else if−else if…
  3. 嵌套条件语句

循环语句中布尔表达式翻译

现需要翻译语句：while a<b do if c<d then X:=Y+Z

100:if a<b goto E.true
101:goto E.false
102:if c<d goto 104
103:goto 106
104:t1:=Y+Z
105:X:=t1
106:goto 100
107:…

分析到状态块的开始就可以确认E.true=102，而分析完状态块的结束之后就可以确认E.false=107

for循环语句翻译

现需要翻译语句：for I :=1 step 1 until Y do X:=X+1
等价于C语言的：for(I=1;I<=Y;++I) X=X+1;

100:I:=1
101:goto 103
102:I:=I+1
103:if I<=Y goto 105
104:goto 108
105:T:=X+1
106:X:=T
107:goto 102
108:…

数组的翻译

对于一个静态的n维数组，要访问其中一个元素，可以使用下标法：

A[i1,i2,…,in]

由于内存是一维连续空间，对于行主数组，比如一个2×32×3的二维数组，在内存中的布局为:

A[1,1]A[1,2]A[1,3]A[2,1]A[2,2]A[2,3]

现知道数组A的地址为a，那A[i,j]的地址为：

a+(i−1)×3+(j−1)

设B为n维数组B[l1:u1,l2:u2,…,ln:un]

显然di=ui−li+1。令b是数组首元素地址，那么行主数组下B[i1,i2,…,in]的地址D为：

D=b+(i1−l1)d2d3…dn+(i2−l2)d3…dn+(in−1−ln−1)dn+(in−ln)

对式子展开可以提取出式子中的固定部分和变化部分：
D=constPart+varPart
constPart=b−C
C=l1d2d3…dn+l2d3…dn+…+ln−1dn−1+lndn
varPart=i1d2d3…dn+i2d3…dn+…+in−1dn−1+indn

访问数组元素A[i1,i2,…,in]需要产生两组计算数组的四元式：

  1. 一组计算varPart，存放结果到临时单元T中
  2. 一组计算constPart，存放结果到另一个临时单元T1中

用T1[T]表示数组元素的地址

变址取数的四元式：(=[],T1[T],−,X),相当于X:=T1[T]
变址存数的四元式：([]=,X1,−,T1[T]),相当于T1[T]:=X

现在有一个10*20的数组A，即d1=10,d2=20。则X:=A[I,J]的四元式序列为：
(∗,I,20,T1)
(+,T1,J,T1)
(−,A,21,T2)
(=[],T2[T1],−,T3)
(:=,T3,−,X)

对应：
varPart=20∗I+J
constPart=A−(1∗20+1)=A−21

符号表

符号表的作用

符号表用来体现作用域与可见性信息

  • 登记各类名字的信息
  • 编译各阶段都需要使用符号表
    • 一致性检查和作用域分析
    • 辅助代码生成

符号表的作用：
① 收集符号属性；（词法分析）
② 上下文语义的合法性检查的依据；（语法分析）
③ 作为目标代码生成阶段地址分配的依据；（语义分析）

符号表的组织

符号表的每一项（入口）包含两大栏

  • 名字栏：主栏、关键字栏
  • 信息栏：记录相应的不同属性、分为若干子栏

按名字的不同种属建立多张符号表，如常数表、变量名表、过程名表

符号表中语言符号可分为关键字（保留字）符号，操作符符号及标识符符号

符号表中的标识符一般设置的属性项目有：
① 符号名
② 符号的类型
③ 符号的存储类别
④ 符号的作用域及可视性
⑤ 符号变量的存储分配信息
⑥ 符号的其它属性

符号表操作

针对符号表的常见操作：

• 创建符号表 在编译开始，或进入一个作用域

• 插入表项 在遇到新的标识符声明时进行

• 查询表项 在引用标识符时进行

• 修改表项 在获得新的语义值信息时进行

• 删除表项 在标识符成为不可见或不再需要它的任何信息时进行

释放符号表空间 在编译结束前或退出一个作用域

对符号表进行操作的时机

  • 定义性出现：int index
  • 使用性出现：if index < 100

实现符号表的常用数据结构

• 一般的线性表：如：数组，链表，等
• 有序表：查询较无序表快，如可以采用折半查找
• 二叉搜索树
• Hash表

作用域和可见性

静态语义分析

静态语义： 刻画程序在静态一致性或完整性方面的特征；仅当程序通过了静态语义检查，才能完成后续的中间代码生成和目标代码优化。

主要任务

  • 类型检查（type checks）
    检查每个操作是否遵守语言类型系统的定义

  • 名字的作用域（scope）分析
    建立名字的定义和使用之间联系

  • 控制流检查（flow-of-control checks）
    控制流语句必须使控制转移到合法的地方（如 break语句必须有合法的语句包围它）

  • 唯一性检查（uniqueness checks）
    很多场合要求对象只能被定义一次（如枚举类型的元素不能重复出现）

  • 名字的上下文相关性检查（name-related checks）
    某些名字的多次出现之间应该满足一定的上下文相关性

类型检查

类型检查程序（type checker）负责类型检查

• 验证程序的结构是否匹配上下文所期望的类

• 为相关阶段搜集及建立必要的类型信息

• 实现某个类型系统（type system）