查询优化概述

查询优化的意义

SQL语言具有非过程化特性（必要性）
查询操作存在多解性（可能性）
- 同一个查询语句可以用多种关系代数表达式来表达
- 同一个关系操作可以有多种实现算法或存取路径
  - 选择——全表扫描、索引扫描
  - 自然连接——嵌套循环、排序-合并、索引连接、哈希连接

自然连接算法

自然连接：是一种特殊的等值连接，它要求两个关系进行比较的分量必须是相同的属性组，并且在结果集中将重复属性列去掉。

1）等值连接必须要有等值的条件，当条件不同时连接的结果也不相同，两个关系可以没有相同的属性列
2）自然连接必须要有相同的属性列才能进行，即等值连接之后要去除相同的属性列

嵌套循环算法

for each row1 from T1
	for each row2 from T2
	if row2 match row1//如果row2与row1满足连接条件
	join row1 and row2 into result//加入结果集

简单通用，对参与连接的表没有要求。由于对内层循环表需要进行多次扫描。因此性能较差

排序—合并算法

访问次数：两张表都只会访问0次或1次。
驱动表是否有顺序：无。
是否要排序：是。
应用场景：当结果集已经排过序。

如果A表的数据为（2,1,4,5,2）,B表的数据为(2,2,1,3,1) ,首先将A表和B表全扫描后排序，如下：

A B

1 1

2 1

2 2

4 2

5 3

因为没有驱动表，所以数据库会随机选择一张表驱动，如果选择了A扫描到1，然后扫描B，当扫描=1的时候则匹配

当扫描到B=2时，再以B=2为驱动扫描A表，不是从1开始扫，而是从2开始扫描，交替的进行扫描、关联。

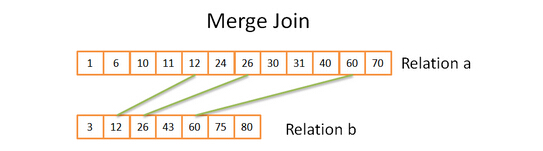
也就是说：不是从1重新开始扫，而是从2开始扫描

对于左表和右表只需要扫描一遍，性能比较高。但是只适用于参与连接的表已经有序的情况。

索引连接算法

利用索引提高连接过程中的元组查找速度，适用于参加连接的表的连接属性上存在索引的情况。

哈希连接算法

通过对连接属性进行哈希分桶来提高连接阶段的匹配速度，适用于较小的那个连接表在散列后能完全放入内存的情况

简单的对于两个表来讲，hash-join就算讲两表中的小表（称S）作为hash表，然后去扫描另一个表(称M)的每一行数据，用得出来的行数据根据连接条件去映射建立的hash表，hash表是放在内存中的，这样可以很快的得到对应的S表与M表相匹配的行。

对于结果集很大的情况，merge-join需要对其排序效率并不会很高，而nested loop join是一种嵌套循环的查询方式无疑更不适合大数据集的连接，而hash-join正是为处理这种棘手的查询方式而生，尤其是对于一个大表和一个小表的情况，基本上只需要将大小表扫描一遍就可以得出最终的结果集。

　　不过hash-join只适用于等值连接，对于>, <, <=, >=这样的查询连接还是需要nested loop这种通用的连接算法来处理。如果连接key本来就是有序的或者需要排序，那么可能用merge-join的代价会比hash-join更小，此时merge-join会更有优势。

代数优化

是指通过对关系代数表达式的等价变换来提高查询效率

就是查询语法树的等价变形

变换五大核心规则

总结起来就是: “(连接类的)交换律, 结合律; (投影和选择类的)串接律, (这两大类相互之间)分配率”

E1 X E2 = E2 X E1, (E1 X E2) X E3 = E1 X (E2 X E3)做笛卡尔积, 多个表做连接是满足交换律和结合律的
投影和选择的串接定律
多层的投影可以取小的那个
多层的选择可以取交集(其实也是那个范围比较小的), 这样能够把多次选择多次表的扫描, 改成一次.
选择与投影交换律: 选择和投影的顺序可以随意改变
选择与笛卡尔积, 并, 自然连接, 差的分配律: 处在后面的选择, 可以与处在前面的二目运算顺序进行调整, 使得对相应的表先实施选择, 再实现连接等二目运算. 这个非常重要, 是先选择后进行二目运算的依据, 又名”选择提前”.
选择与笛卡尔积, 并的分配率: 可以先投影, 也可以先进行二目运算

导致关系数据库查询性能低的主要原因是笛卡尔积运算

投影与交运算不属于关系代数表达式等价规则

经验性优化五大策略

其实就是”选择, 合并, 视图”

选择运算尽可能先做, 这是最最最最重要和基本的, 这样往往使得执行代价减少了几个数量级, 主要的原理就是选择运算能够大大降低参与连接的元组的行数, 使得连接生成的A•B结果也大大被缩小.
把选择和投影运算同时进行, 如果有若干投影和选择运算, 并且他们都是针对同一个表, 那么可以在扫描这个表的时候同时完成这些所有的运算, 以此避免重复扫描这张表.
把投影与其前或者后的双目运算(笛卡尔积, 等值连接, 并集, 差集)结合起来, 也就是说, 没有必要为了选择出几个字段而单独再重新扫描全表.
把某些选择和在它前面要执行的笛卡尔积结合起来成为一个连接运算(比如变成等值连接), 这是因为连接运算要比同样情形下的笛卡尔积节省很多时间.

笛卡尔积先进行了 O(N • M)操作生成了A•B大小的中间文件, 存盘, 然后读盘, 然后再按照where选择进行筛选得到结果; 对比之下, 等值连接运算也进行了O(N•M)操作, 但是还进行了筛选, 只生成比较小的中间文件, 存盘和读盘的是一个非常小的结果集合. 大大减少了IO开销.

找出公共子表达式(一次计算, 多次使用). 比如很多的查询都基于某个公共部分, 那么可以定义一个公共子表达式, 然后先计算一次公共子表达式, 然后把它存盘, 供其他大量的表达式来使用. 我们定义视图其实就是在实践这种策略.

物理优化

基于经验规则的优化

对于小的表, 直接全表扫描, 即使列上有索引.
对于大的表：
- 如果是选择条件涉及主键, 那么使用主键索引(MySQL等主流关系数据库都会对主键建立索引);
- 如果不是涉及主键：
  - 如果是等值查询, 列上有索引, 就使用索引;
  - 如果非等值查询, 而是范围值查询, 那么范围<=10%用索引, 范围比较大的, 直接全表扫描.
And 和 OR:
- AND连接的, 优先考虑使用索引;
- OR连接的, 优先考虑使用顺序扫描, 毕竟OR可能性非常多.
连接操作:
- 如果两个表都按照连接属性排序, 用sort-merge算法
- 如果其中一个表在连接属性上有索引,采用索引连接算法;
- 如果啥都没有, 对小的表建立哈希表, 使用hash join方法; 或者使用基本的嵌套循环, 不过外层循环(i循环)使用小表, 这样能稍微减小代价.

基于代价的优化

基于代价的优化需要依赖数据库表的各种”情报”, 来计算出不同方案的代价, 从中选择最优的.
这些信息(meta info)包括:

对每个表来说:
表的元组行数 N,
元组的长度, 即列的维度数目 P,
表占用的block数目 B,
表占用的溢出块的块数 BO,
对表中的每个列,
该列的不同值的个数 k
列的最大值, 最小值max, min
列上有什么类型的索引 index: 按照实现方式有B+, Hash, Cluster / 按照类型来说有普通索引, 唯一索引, 主键索引, 聚集索引
列上的数值分布情况 (直方图)

那么对于不同情况, 我们有如下的代价估算:

全表扫描 cost = B
有索引的扫描
如果选择条件是key = value, 能适用唯一索引: L + 1
如果选择条件是attr = value, 能使用普通索引: L + S (可能有S个元组满足)
如果条件是范围类的, 比如>, <, between A and B, 那么基本上就是接近全表扫描B;
连接算法的代价
如果用嵌套循环: 读入Capacity-1块B[a], 遍历连接b表所有B[b], 再换下一批B[a], 直到a表结束. 所以, cost = B[a] + ( B[a]/(C-1) ) • B[b] = a表IO次数 + b表IO次数, 假如要生成中间文件的话, 那么还得加上存下所有连接好的元组的磁盘IO开销.

如果用sort-merge: cost = B[a] + B[b], 如果要把中间结果写入外存, 那么还要加上存下所有连接好的元组的磁盘IO开销, 这个开销和上面嵌套循环的是一样的.
假如表本身没有排序, 那么排序的代价是B[a]logB[a] + B[b]logB[b]

rhb_blog

数据库_查询处理和查询优化