优化技术介绍

代码优化，是指对中间代码或目标代码进行等价变换，使得变换后的代码运行速度加快和存储空间减少。

代码优化按照优化的代码块尺度分为：局部优化、循环优化和全局优化。即

局部优化：只有一个控制流入口、一个控制流出口的基本程序块上进行的优化；
循环优化：对循环中的代码进行的优化；
全局优化：在整个程序范围内进行的优化。

常见的代码优化手段

常见的代码优化技术有：删除多余运算、合并已知量和复写传播，删除无用赋值等。

针对目标代码：

1
2
3

P := 0
for I := 1 to 20 do 
    P := P + A[I]*B[I]

假设其翻译所得的中间代码如下

删除多余运算
分析上图的中间代码，可以发现(3)和式(6)属于重复计算（因为I并没有发生变化），故而式(6)是多余的，完全可以采用T4∶=T1代替。
代码外提
减少循环中代码总数的一个重要办法是循环中不变的代码段外提。这种变换把循环不变运算，即结果独立于循环执行次数的表达式，提到循环的前面,使之只在循环外计算一次。针对改定的例子，显然数组A和 B的首地址在计算过程中并不改变，则作出的改动如下

强度削弱
强度削弱的本质是把强度大的运算换算成强度小的运算，例如将乘法换成加法运算。针对上面的循环过程，每循环一次，I的值增加1，T1的值与I保持线性关系，每次总是增加4。因此，可以把循环中计算T1值的乘法运算变换成在循环前进行一次乘法运算，而在循环中将其变换成加法运算。

变换循环控制条件
I和T1始终保持T1＝4*I的线性关系，因此可以把四元式（12）的循环控制条件I≤20变换成T1≤80，这样整个程序的运行结果不变。这种变换称为变换循环控制条件。经过这一变换后，循环中I的值在循环后不会被引用，四元式（11）成为多余运算，可以从循环中删除。变换循环控制条件可以达到代码优化的目的。
合并已知量和复写传播
四元式（3）计算4 * I时，I必为1。即4*I的两个运算对象都是编码时的已知量，可在编译时计算出它的值，即四元式（3）可变为T1＝4，这种变换称为合并已知量。

四元式(6)把T1的值复写到T4中，四元式（8）要引用T4的值，而从四元式（6）到四元式（8）之间未改变T4和T1的值，则将四元式（8）改为T6∶=T5[T1]，这种变换称为复写传播。

删除无用赋值
式（6）对T4赋值，但T4未被引用；另外，（2）和（11）对I赋值，但只有（11）引用I。所以，只要程序中其它地方不需要引用T4和I，则（6），（2）和（11）对程序的运行结果无任何作用。我们称之为无用赋值，无用赋值可以从程序中删除。至此，我们可以得到删减后简洁的代码

基本块内的局部优化

基本块的划分

入口语句的定义如下：
　　① 程序的第一个语句；或者，
　　② 条件转移语句或无条件转移语句的转移目标语句；
　　③ 紧跟在条件转移语句后面的语句。
有了入口语句的概念之后，就可以给出划分中间代码（四元式程序）为基本块的算法，
　　其步骤如下：
　　① 求出四元式程序中各个基本块的入口语句。
　　② 对每一入口语句，构造其所属的基本块。它是由该入口语句到下一入口语句（不包括下一入口语句），或到一转移语句（包括该转移语句），或到一停语句（包括该停语句）之间的语句序列组成的。
　 ③ 凡未被纳入某一基本块的语句、都是程序中控制流程无法到达的语句，因而也是不会被执行到的语句，可以把它们删除。

基本块的优化手段

由于基本块内的逻辑清晰，故而要做的优化手段都是较为直接浅层次的。目前基本块内的常见的块内优化手段有：

删除公共子表达式
删除无用代码
重新命名临时变量（一般是用来应对创建过多临时变量的，如t2 := t1 + 3如果后续并没有对t1的引用，则可以t1 := t1 + 3来节省一个临时变量的创建）
交换语句顺序
在结果不变的前提下，更换代数操作（如$x∶=y2$是需要根据 $$运算符重载指数函数的，这是挺耗时的操作，故而可以用强度更低的$x∶=y*y$来代替）

根据以上原则，对如下代码进行优化

t1 := 4 - 2
t2 := t1 / 2 
t3 := a * t2
t4 := t3 * t1
t5 := b + t4
 c := t5 * t5

给出优化的终版代码

1
2
3

t1 := a + a
t1 := b + t1
 c := t1 * t1

显然代码优化的工作不能像上面那样的人工一步步确认和遍历，显然必然要将这些优化工作公理化。而一般到涉及到数据流和控制流简化的这种阶段，都是到了图论一展身手的时候。

DAG（无环路有向图）应用于基本块的优化工作

利用DAG进行基本块优化的基本思想是：按照构造DAG结点的顺序，对每一个结点写出其相应的三地址代码表示

在DAG图中，通过节点间的连线和层次关系来表示表示式或运算的归属关系：
① 图的叶结点，即无后继的结点，以一标识符（变量名）或常数作为标记，表示这个结点代表该变量或常数的值。如果叶结点用来代表某变量A的地址，则用addr（A）作为这个结点的标记。
② 图的内部结点，即有后继的结点,以一运算符作为标记，表示这个结点代表应用该运算符对其后继结点所代表的值进行运算的结果。
（注：该部分内容转载自教材《编译原理》第11章DAG无环路有向图应用于代码优化）

DAG构建的流程如下

对基本块的每一四元式，依次执行：
　　1．

如果NODE（B）无定义，则构造一标记为B的叶结点并定义NODE（B）为这个结点；
　　如果当前四元式是0型，则记NODE（B）的值为n，转4。
　　如果当前四元式是1型，则转2.（1）。
　　如果当前四元式是2型，则：（Ⅰ）如果NODE（C）无定义，则构造一标记为C的叶结点并定义NODE（C）为这个结点，（Ⅱ）转2.（2）。
　　2．
　　（1）如果NODE（B）是标记为常数的叶结点，则转2.（3），否则转3.（1）。
　　（2）如果NODE（B）和NODE（C）都是标记为常数的叶结点，则转2.（4），否则转3.（2）。
　　（3）执行op　B（即合并已知量），令得到的新常数为P。如果NODE（B）是处理当前四元式时新构造出来的结点，则删除它。如果NODE（P）无定义，则构造一用P做标记的叶结点n。置NODE（P）＝n，转4.。
　　（4）执行B　op　C(即合并已知量)，令得到的新常数为P。如果NODE（B）或NODE（C）是处理当前四元式时新构造出来的结点，则删除它。如果NODE（P）无定义，则构造一用P做标记的叶结点n。置NODE（P）＝n，转4.。
　　3．
　　（1）检查DAG中是否已有一结点，其唯一后继为NODE（B），且标记为op（即找公共子表达式）。如果没有，则构造该结点n，否则就把已有的结点作为它的结点并设该结点为n，转4.。
　　（2）检查DAG中是否已有一结点，其左后继为NODE（B），右后继为NODE（C），且标记为op(即找公共子表达式)。如果没有，则构造该结点n，否则就把已有的结点作为它的结点并设该结点为n。转4.。
　　4．
　　如果NODE（A）无定义，则把A附加在结点n上并令NODE（A）＝n；否则先把A从NODE（A）结点上的附加标识符集中删除（注意，如果NODE（A）是叶结点，则其标记A不删除），把A附加到新结点n上并令NODE（A）＝n。转处理下一四元式。

说着很复杂，下面看一个案例

(1) T0∶=3.14
(2) T1∶=2 * T0
(3) T2∶=R + r
(4) A∶=T1 * T2
(5) B∶=A
(6) T3∶=2 * T0
(7) T4∶=R + r
(8) T5∶=T3 * T4
(9) T6∶=R - r
(10) B∶=T5 * T6

其DAG图的构建过程如下

通过DAG图可以发现诸多的优化信息，如重复定义、无用定义等，则根据上图的DAG图可以构建最后的优化代码序列

　　(1) S1∶=R+r
　　(2) A∶=6.28*S1
　　(3) S2∶=R-r
　　(4) B∶=A *S2

循环优化

循环优化的主要手段有：循环次数无关性代码外提、删除归纳变量和运算强度削弱。关于这三种手段的理解可以借助此前的描述进行类比，基本并无太多差异。

流图

结点是基本块的有向图G = ( N, E, root)

N是结点的集合，每个结点表示一个基本块
E是边的集合，如果结点ni和nj间存在前驱和后继的关系，则在存在一条从ni到nj的有向边（此时意味着，在ni执行后，可能会执行nj）
- ni的出口语句是goto(s)或if … goto(s)，且(s)是的nj入口语句
- nj在程序中的位置紧跟在ni后，且ni的出口语句不是无条件转移语句和停语句
root是流图的首结点（或称为根结点），是包含程序第一个语句的基本块

每个流图都可以等价变换为单入口，且每个结点最多有两个后继的图

根据上面基本块的定义，我们将诸多基本块组装在一起，构建成程序循环图，如针对下面这个例子

　　(1) read x
　　(2) read y
　　(3) r∶=x mod y
　　(4) if r=0 goto (8)
　　(5) x∶=y
　　(6) y∶=r
　　(7) goto (3)
　　(8) write y
　　(9) halt

则按照上面基本块的划分，可以分成四个部分，四个部分的控制流分析可知可以得到一个循环图（流图）

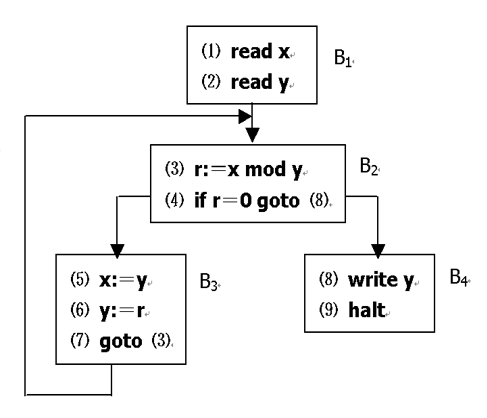
循环块最主要的特点是只有一个数据流和控制流入口，而出口可能有多个。

rhb_blog

编译原理-代码优化和目标代码生成