流水线的基本概念

流水线的段（级）：流水线中的每个子过程及其功能部件称为流水线的级或段，段与段相互连接形成流水线
流水线的瓶颈：执行时间最长的段
流水线的深度：流水线的段数称为流水线的深度
流水线的通过时间：第一个任务从进入流水线到流出结果所需的时间。
排空时间：最后一个任务从进入流水线到流出结果所需的时间。

流水线不适用的场景：

只有一个任务需要执行。【任务并没有在更短的时间内完成，反而有可能会使得单个任务的执行时间变长】
多个稀疏任务（来的不够密集）。【使用流水线并不能提升工作效率（执行这些任务的有效时间并没有缩短）】
多个不同任务。【多个密集任务，但各任务的子过程完全无重合（不能使用同一部件处理）】

但是可以通过其它并行技术加速（增加更多的不同部件，使得不同任务的不同子过程能并行执行）

流水线适用的场景：

多个密集且相同或类似的任务。【流水技术适合于大量重复的时序过程，只有在输入端不断地提供任务，才能充分发挥流水线的效率。】

流水线的分类

按用于计算机系统的等级划分，流水线可分为：部件级、处理机级及处理机间流水线

部件级流水线（运算操作流水线）

把处理机中的部件分段，再把这些分段相互连接起来，使得各种类型的运算操作能够按流水方式进行。

eg：浮点加法流水线，包含4个段：求阶差，对阶，尾数相加，规格化
处理机流水线（指令流水线）

把指令的执行过程按照流水方式处理。把一条指令的执行过程分解为若干个子过程，每个子过程在独立的功能部件中执行。

eg：经典5段MIPS指令流水线，包含5个段：取址，译码，执行，访存，写回。
处理机间流水线（宏流水线）

把多台处理机串行连接起来，对同一数据流进行处理，每个处理机完成整个任务中的一部分。

eg：map reduce

按流水线所完成的功能可划分为：单功能流水线与多功能流水线

单功能流水线：只能完成一种固定功能的流水线
多功能流水线：流水线的各段可以进行不同的连接，以实现不同的功能【某些段可以不执行，直接跳过】。
- 静态流水线：在同一时间内，多功能流水线中的各段只能按同一种功能的连接方式工作。
- 动态流水线：在同一时间内，多功能流水线中的各段可以按照不同的方式连接，同时执行多种功能

按流水线中是否有反馈回路，流水线技术可分为线性流水线与非线性流水线

线性流水线：若流水线的各段串行连接，没有反馈回路，则其为线性流水线。再线性流水线中，数据通过流水线中的各段时，每一个段最多只流过一次。
非线性流水线：若流水线中除了有串行的连接外，还有反馈回路，则其为非线性流水线。

按任务流入和流出的顺序是否相同划分：顺序流水线与乱序流水线

顺序流水线：流水线输出端任务流出的顺序与输入端任务流入的顺序完全相同。每一个任务在流水线的各段中是一个跟着一个顺序流动的。
乱序流水线：流水线输出端任务流出的顺序与输入端任务流入的顺序可以不同，允许后进入流水线的任务先完成（从输出端流出）。

流水线的性能指标

吞吐率TP

吞吐率通常使用缩写TP表示，是指在单位时间内流水线所完成的任务数量或输出结果的数量。
$$
TP=\frac{n}{T_k}\
n:任务数\
T_k:处理完成n个任务所用的时间
$$

CPU的吞吐率是指CPU每秒执行的指令数。

分析

假设各段时间均等：

（k段线性）流水线完成n个连续任务所需要的总时间
$$
T_k=(k+n-1)\Delta t\
k\Delta t:流水线通过时间\
(n-1)\Delta t:流水线排出时间\
实际吞吐率：TP=\frac{n}{(k+n-1)\Delta t}\
最大吞吐率：TP_{max}=\lim_{n\to\infty}{\frac{n}{(k+n-1)\Delta t}}=\frac{1}{\Delta t}\
当n趋近于无穷大时，流水线吞吐率趋近于最大值（又称流水线的最大吞吐率）\
TP=\frac{n}{(k+n-1)}TP_{max}
$$
假设各段时间不全相等：

（k段线性）流水线完成n个连续任务所需要的总时间
$$
T_k=\sum\Delta t_i+(n-1)max(\Delta t_i)\quad (i=1,2,3···k)\
\sum\Delta t_i:单个任务的执行时间(通过时间)\
(n-1)max(\Delta t_i):n-1个瓶颈段的执行时间\
实际吞吐率：TP=\frac{n}{\sum\Delta t_i+(n-1)max(\Delta t_1,\Delta t_2,···\Delta t_k)}\
最大吞吐率：TP_{max}=\frac{1}{(n-1)max(\Delta t_1,\Delta t_2,···\Delta t_k)}\
$$

流水线瓶颈问题

流水线中执行时间最长的段称为流水线的瓶颈段

瓶颈段使得流水线性能下降

解决流水线瓶颈的方法

细分瓶颈段（细分流水线）
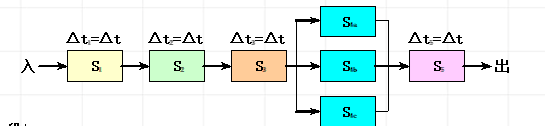
重复设置瓶颈段

细分瓶颈段

就是降低：$(n-1)max(\Delta t_i)$的值。将数值大的$\Delta t_i$值进行细分，差分成数值更小的$\Delta t_i$

重复设置瓶颈段

就是在采取同时多次进行瓶颈段的操作来降低$\Delta t_i$

加速比S

完成同样一批任务，不使用流水线所用的时间与使用流水线所用的时间之比。
$$
S=\frac{T_s}{T_k}\
T_s：不使用流水线（即顺序执行）所用的时间\
T_k：使用流水线后所用的时间
$$

分析

假设各段时间均等

$$
一条k段流水线完成n个连续任务所需要的时间:T_k=(k+n-1)\Delta t\
顺序执行n个任务所需要的时间：T_s=nk\Delta t\
实际加速比：S=\frac{nk}{n+k-1}\
最大加速比：S_{max}=\lim_{n\to\infty}\frac{nk}{k+n-1}=k
$$
假设各段时间不全相等
$$
实际加速比：S=\frac{n\sum_{i=1}^{k}\Delta t_i}{\sum_{i=1}^{k}\Delta t_i+(n-1)max(\Delta t_1,\Delta t_2,···\Delta t_k)}\
$$
每段执行时间并不完全相等，那么流水线完成n个连续任务所需要的总时间Tk等于单个任务的执行时间（通过时间），加上n-1个瓶颈段的执行时间。而顺序执行这n个任务，所需要的时间为n倍的单个任务的执行时间。

效率E

流水线中的设备实际使用时间与整个运行时间的比值。

【由于流水线有通过时间和排空时间，所以在连续完成n个任务的时间内，各段并不是满负荷地工作】

分析

各段时间均等：

假设各段的效率ei 相等
$$
e_1=e_2=e_3=···=e_k=\frac{n\Delta t}{T_k}=\frac{n}{k+n-1}\
整条流水线的效率：E=\frac{e_1+e_2+e_3+···+e_k}{k}=\frac{ke_1}{k}=\frac{n}{k+n-1}\
$$

效率和其他指标的关系

当流水线各段时间相等时，流水线的效率与吞吐率成正比$E=TP·\Delta t$

流水线的效率是流水线的实际加速比S与它的最大加速比k的比值$E=\frac{S}{K}$

直观的描述：
$$
E=\frac{n个任务实际占用的时空区}{k个段总的时空区}
$$
各段时间不全相等：
$$
E=\frac{n\sum_{i=1}^{k}\Delta t_i}{K[\sum_{i=1}^{k}\Delta t_i+(n-1)max(\Delta t_1,\Delta t_2,···\Delta t_k)]}\
$$

多功能流水线性能指标

影响（多功能）流水线性能的原因

–多功能流水线在做某一种运算时，总有一些段是空闲的；

–静态流水线在进行功能切换时，要等前一种运算全部流出流水线后才能进行后面的运算；

–运算之间存在关联，后面有些运算要用到前面运算的结果；

流水线的工作过程有建立与排空部分。

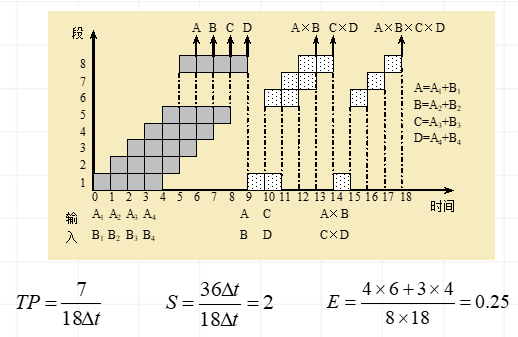
eg：设在下图所示的静态流水线上计算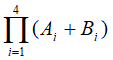的吞吐率、效率和加速比

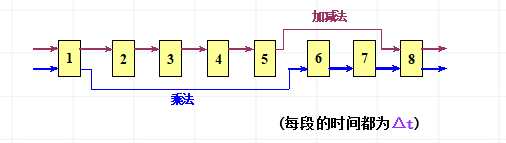
选择适合于流水线工作的算法

先计算A1+B1、A2+B2、A3+B3和A4+B4；再计算(A1+B1)×(A2+B2)和(A3+B3)×(A4+B4)；然后求总的乘积结果。

流水线设计中的重要问题

瓶颈问题

理想情况下，流水线在工作时，其中的任务是同步地每一个时钟周期往前流动一段。
当流水线各段不均匀时，机器的时钟周期取决于瓶颈段的延迟时间。
在设计流水线时，要尽可能使各段时间相等。

流水线的额外开销

流水寄存器需要建立时间和传输延迟
- 建立时间：在触发写操作的时钟信号到达之前，寄存器输入必须保持稳定的时间。
- 传输延迟：时钟信号到达后到寄存器输出可用的时间。
时钟偏移开销
- 流水线中，时钟到达各流水寄存器的最大差值时间。（时钟到达各流水寄存器的时间不是完全相同）

由流水线性能与开销得到的重要结论

流水线并不能减少（而且一般是增加）单条指令的执行时间，但却能提高吞吐率。
增加流水线的深度（段数）可以提高流水线的性能。
流水线的深度受限于流水线的额外开销。
当时钟周期小到与额外开销相同时，流水已没意义。因为这时在每一个时钟周期中已没有时间来做有用的工作。【所以，流水段的段数越多不一定就越好】

单功能非线性流水线的调度

基本概念

启动距离：向一条非线性流水线的输入端连续输入两个任务之间的时间间隔称为非线性流水线的启动距离。
禁用启动距离：会引起非线性流水线功能段使用冲突的启动距离则称为禁用启动距离。

启动距离和禁用启动距离一般都用时钟周期数来表示，是一个正整数。

除去禁用启动距离外，其它的启动距离都是可用的，这也意味着，若两个任务进入非线性流水线的时间间隔不是禁用启动距离，那么这两个任务之间不会产生冲突。

预约表：时间和执行的功能段之间的二维表
禁止表F：一个由禁用启动距离构成的集合

对于预约表的每一行的任何一对√，用它们所在的列号相减（大的减小的），列出各种可能的差值，然后删除相同的，剩下的就是禁止表的元素。

冲突向量

冲突向量：一个N位的二进制位串：

初始冲突向量C0 决定了下一个任务需间隔多少个时钟周期才可以流入

设C0=（cNc~~N-1~~…ci…c2c1）;$C_i=\begin{cases}1,&i\in F\0,&i\notin F\end{cases}$
ci=0 ：允许间隔i个时钟周期后送入后续任务
ci=1 ：不允许间隔i个时钟周期后送入后续任务

假设第二个任务是在与第一个任务间隔j个时钟周期流入，这时，由于第一个任务已经在流水线中前进了j个时钟周期，其相应的禁止表中各元素的值都应该减去j，并丢弃小于等于0的值。对原始冲突向量C0来说，就是逻辑右移j位（左边补0）。

第二个任务也会有着自己的冲突向量C。

由于后续任务既不能与第一个任务冲突，又不能与第二个任务冲突，所以当前（第二个任务进入流水线后的那个时钟周期）冲突向量（禁止表）是第一个任务与第二个任务的当前冲突向量的按位或（并集）。

假设: Ck为当前的冲突向量，j: 允许的时间间隔，则，新的冲突向量为：SHR(j)（Ck）∨C0（将当前冲突向量逻辑右移j位，再与新任务的冲突向量C0做按位或），得到，任意一个任务进入后的新冲突向量。

（通过遍历）获得所有可能的冲突向量，构成流水线状态集合：

从初始冲突向量C0出发，对于所有允许的时间间隔（所有i，满足Ci=0）都按上述步骤求出其新的冲突向量，并且把新的冲突向量作为当前冲突向量，反复使用上述步骤，直到不再产生新的冲突向量为止。

流水线状态转移图

得到所有可能的冲突向量后，可以画出其状态转移图。

三要素

流水线状态集合（所有可能的冲突向量）
有向弧：表示状态转移的方向
弧上的数字：表示引入后续任务（从而产生新的冲突向量）所用的时间间隔（时钟周期数）

调度方案与最优调度方案

调度方案：根据流水线状态图，由初始状态出发，任何一个闭合回路即为一种调度方案。
最优调度方案：（任务进入流水线的）平均时间间隔最小的调度方案

列出所有可能的调度方案，计算出每种方案的平均时间间隔，从中找出其最小者即为最优调度方案。

等时间间隔调度方案

不等时间间隔的调度方案，与等间隔的调度方案相比，在控制上要复杂得多。

流水线冲突

流水线冲突是指对于具体的流水线来说，由于相关等原因的存在使得指令流中的下一条指令不能在指定的时钟周期执行。

流水线冲突分类

结构冲突：因硬件资源满足不了指令重叠执行的要求而发生的冲突。
数据冲突：当指令在流水线中重叠执行时，因需要用到前面指令的执行结果而发生的冲突。
控制冲突：流水线遇到分支指令和其它会改变PC值的指令所引起的冲突。

问题与基本解决方法

问题

导致错误的执行结果。
流水线可能会出现停顿，从而降低流水线的效率和实际的加速比。

基本解决方法

暂停部分指令执行：当一条指令被暂停时，在该暂停指令之后流出的所有指令都要被暂停，而在该暂停指令之前流出的指令则继续进行（否则就永远无法消除冲突）。

结构冲突

常见的导致结构冲突的原因有两个。一是功能部件不是完全流水，二是资源份数不够。

解决方法：

插入暂停周期【通过拉开两条冲突指令在流水线之间的距离来避免冲突发生的】
- 为消除结构冲突而插入的流水线气泡
设置相互独立的存储器，使之分别存储指令与数据【通过增加资源数量，来避免访问同一资源导致的冲突】
- 通过让读取指令与读写数据的访存请求落到不同的存储器中，从而避免访问同一存储器引起的冲突。对应的就是组成原理课程中讲过的哈弗结构。在现代通用处理器中，这种技术被普遍用于一级cache中。

不一定需要消除所有的结构冲突：

主要是为了考虑减少硬件成本。

数据冲突

写后读冲突（RAW）

对应的相关：最常见的一种数据冲突，对应于真数据相关。

发生条件

有两条指令i和j，i在j之前进入流水线
在 i 写入之前，j 先去读

结果

j 读出的内容是错误的

写后写冲突（WAW）

对应相关：对应于输出相关。

发生条件：

流水线中不只一个段可以进行写操作，且指令被重新排序了
有两条指令i和j，i在j之前进入流水线
在 i 写入之前，j 先写。

结果

最后写入的结果是 i 的。错误！

读后写冲突（WAR）

对应相关：反相关

发生条件

有些指令的写结果操作提前了，而且有些指令的读操作滞后了；或是指令被重新排序了。
有两条指令i和j，i在j之前进入流水线。在 i 读取之前，j 先写入。

结果

i读到的结果是错误的。

解决方案

定向（短路、旁路）：（减少冲突引起的停顿时间）
- 在计算结果尚未出来之前，后面等待使用该结果的指令并不真正立即需要该计算结果，如果能够将该计算结果从其产生的地方直接送到其它指令需要它的地方，那么就可以避免停顿。

定向技术实际上是在原有的寄存器传递数据的基础上，增加了新的指令间传递数据的路径。

指令调度（流水线调度）：让编译器重新组织指令顺序来消除冲突

定向技术是基于硬件的运行时解决方案；指令调度是基于软件的的预处理方案

控制冲突

起因：执行分支指令的结果有两种

分支成功：PC值改变为分支转移的目标地址。在条件判定和转移地址计算都完成后，才改变PC值。
不成功或者失败：PC的值保持正常递增，指向顺序的下一条指令。

控制冲突

分支延迟：分支指令引起的延迟

最简单的处理方法

“冻结”或者“排空”流水线
- 前述5段流水线中，改变PC值是在MEM段进行的。给流水线带来了3个时钟周期的延迟

基本解决方案

通过设置专用的处理单元，在流水线中尽早判断出分支转移是否成功，以及分支目标地址。【硬件】

进一步：基于编译器的软件方法

预测分支失败

允许分支指令后的指令继续在流水线中流动，就好象什么都没发生似的；若确定分支失败，将分支指令看作是一条普通指令，流水线正常流动；若确定分支成功，流水线就把在分支指令之后取出的所有指令转化为空操作，并按分支目地重新取指令执行。

预测分支成功

假设分支转移成功，并从分支目标地址处取指令执行。这种方法起作用的前题是，需要先知道分支目标地址，后知道分支是否成功。显然，前述5段流水线中，这种方法没有任何好处。原因在于，分支目标地址与分支是否成功是同时计算出来的。

延迟分支

从逻辑上“延长”分支指令的执行时间。把延迟分支看成是由原来的分支指令和若干个延迟槽构成，不管分支是否成功，都要按顺序执行延迟槽中的指令。
延迟分支的优点在于无论分支成功还是失败都能够减少（掩盖）一个时钟周期的延迟。

通过在分支指令后增加延迟槽，并将有用的指令从别处调度到延迟槽执行，当分支是否成功与分支目标地址被算出时，恰好能够进行对应的取指操作，从而有效的消除了分支延迟。

–要点：在延迟槽中放入有用的指令，由编译器完成。能否带来好处取决于编译器能否把有用的指令调度到延迟槽中。

从调度的角度，延迟分支又可分为三类：从前调度，从目标处调度，从失败处调度。

从前调度：从分支指令之前调度一条与该分支无关的指令到分支延迟槽中。
从目标处调度：将分支目标地址对应的指令调度到延迟槽中。
从失败处调度：将分支失败处的指令（下一条顺序地址）调入延迟槽。

由于只有当调入到延迟槽的指令实际上会被执行时，分支延迟技术才会真正起效，因此，可以认为：无论分支是否成功，从前调度均能消除控制冲突；只有当分支成功时，从目标处调度才能消除控制冲突；只有当分支失败时，从失败处调度才能消除控制冲突。

既然从前调度的效果远胜于后两种调度，为什么还要有后两种方法呢？原因在于，前面提到的从前调度需要找到一条与该分支无关的指令，这样的指令通常是极少的。

分支延迟的改善受到两个方面的限制：一是需要在延迟槽中放入有用的指令（由编译器完成）；二是能否带来好处取决于编译器能否把有用的指令调度到延迟槽中。

此外，对于预测错误的情况，需要进一步的改进。引入分支取消机制，当分支的实际执行方向和事先所预测的一样时，执行分支延迟槽中的指令，否则就将分支延迟槽中的指令转化成一个空操作。

流水线的实现

MIPS的流水化：每一个时钟周期完成的工作看作是流水线的一段，每个时钟周期启动一条新的指令。

流水寄存器的位置和作用：

位置：段与段之间设置流水寄存器
作用
- 将各段的工作隔开，使得它们不会互相干扰。
- 保存相应段的处理结果。
- 向后传递后面将要用到的数据或者控制信息
  所有有用的数据和控制信息每个时钟周期会随着指令在流水线中的流动往后流动一段

流水线的基本概念

流水线的分类

流水线的性能指标

吞吐率TP

分析

流水线瓶颈问题

细分瓶颈段

重复设置瓶颈段

加速比S

分析

效率E

分析

多功能流水线性能指标

流水线设计中的重要问题

瓶颈问题

流水线的额外开销

由流水线性能与开销得到的重要结论

单功能非线性流水线的调度

基本概念

冲突向量

流水线状态转移图

调度方案与最优调度方案

等时间间隔调度方案

相关

数据相关

数据相关检测

名相关

反相关

输出相关

名相关解决方案

控制相关

流水线冲突

问题与基本解决方法

结构冲突

数据冲突

写后读冲突（RAW）

写后写冲突（WAW）

读后写冲突（WAR）

解决方案

控制冲突

基本解决方案

预测分支失败

预测分支成功

延迟分支

流水线的实现