互连网络（ICN）
互连网络是计算机部件、计算机节点或计算机系统之间的连接。
例如：CPU和CPU之间、CPU内的多核之间、CPU和内存之间、内存和内存之间、计算机节点之间、网络和网络之间。
互连网络的直接设计目标是：在最少传输延迟约束内，传输尽可能多的数据，避免成为系统的瓶颈。
高速互连网络（<100s时钟周期）
片上/系统高速互连网络是一种由网络元件按照一定的拓扑结构和控制方式构成的网络，用来实现计算机系统中部件之间的高速连接。
- 三大要素：网络元件、互连结构、控制方式
- 结点：处理器、存储模块或其它设备
- 在拓扑上，互连网络为输入结点到输出结点之间的一组互连或映象。
- 互连结构是静态连接拓扑
- 控制方式是基于静态拓扑结构的动态传输机制
互连网络的主要操作：
- 置换（N-N）
- 广播（1-N）
- 选播（1-部分）
互连网络的结构参数和指标
结构参数
网络通常是用有向边或无向边连接有限个结点的图来表示。
互连网络的主要特性参数：
- 网络规模N：网络中接点的个数
- 结点度d：与结点相连接的边数，包括入度和出度
- 结点距离：对于网络中任意两个结点，从一个结点出发到另一个结点终止所需要跨越的边数的最小值
- 网络直径D：网络中任意两结点间距离的最大值
- 网络直径应尽可能小
- 等分宽度b：把由N个结点构成的网络切成结点数相同（N/2）的两半，在各种切法中，沿切口边数的最小值。
- 线等分宽度：B=b X w，w为通道宽度
- 该参数反映了网络最大流量
- 对称性：从任何结点看到的拓扑结构都相同的网络称为对称网络。
性能指标
时延和带宽
- 通信时延：指从源节点到目的结点传送一条消息所需的总时间
【=软件开销+通道时延+选路时延+竞争时延】 - 网络时延：通道时延与选路时延的和
- 由网络硬件特征决定，与程序行为和网络传输状态无关
- 端口带宽
- 对于互连网络中任意一个端口来说，其端口带宽是指单位时间内从该端口传送到其他端口的最大信息量。
- 聚集带宽
- 网络从一半结点向另一半结点传输时，单位时间内能够传送的最大信息量
互连函数
反映了网络输入数组和输出数组之间对应的置换关系或排列关系（置换函数或排列函数）
变量x：输入 函数f(x)：输出
在互连函数f的作用下，输入端x连接到输出端f(x)
互连函数采用循环表示：（x0,x1,x2,x3,···xj-2,xj-1）表示f(x0)=x1,f(x1)=x2,f(xj-1)=x0
基本的互连函数
恒等函数：实现同号输入端和输出端之间的连接
$I(X_{n-1}X_{n-2}···X_{1}X_{0})=X_{n-1}X_{n-2}···X_{1}X_{0}$交换函数：实现二进制地址编码中第K位互反的输入端和输出端之间的连接
$E(X_{n-1}X_{n-2}···X_{k+1}X_{k}X_{k-1}···X_{1}X_{0})=X_{n-1}X_{n-2}···X_{k+1}\bar{X_{k}}X_{k-1}···X_{1}X_{0}$主要用于构造立方体互连网络和各种超立方体互连网络
供有n=log
2N种互连函数（N为结点个数）$$
Cube_0(x_2x_1x_0)=x_2x_1\overline{x_0}\
Cube_1(x_2x_1x_0)=x_2\overline{x_1}x_0\
Cube_2(x_2x_1x_0)=\overline{x_2}x_1x_0\
$$
均匀洗牌函数（混洗函数、置换函数,shuffle函数）：将输入端分成数目相等的两半，前一半和后一半按类似均匀混洗扑克牌的方式交叉地连接到输出端（输出端相当于混洗的结果）
$\sigma(X_{n-1}X_{n-2}···X_{1}X_{0})=X_{n-2}X_{n-3}···X_{0}X_{n-1}$- 即把输入端的二进制编号循环左移一位
- $shuffle^{n}(j)=j$
- $shuffle_n(j)=j$
子函数和超函数
- 互连函数(s)的第k个子函数s
k：把s作用输入端的二进制编号的低k位 - 互连函数(s)的第k个超函数s^k^：把s作用输入端的二进制编号的高k位
- 互连函数(s)的第k个子函数s
逆函数
- 对于任意一种函数f(x),如果存在g(x)，使得$f(x)\times g(x)=I(x)$。则称g(x)是f(x)的逆函数，记作$f^{-1}(x)=g(x)$
逆均匀洗牌函数：将输入端的二进制编号循环右移一位而得到所连接的输出端编号
$\sigma^{-1}(X_{n-1}X_{n-2}···X_{1}X_{0})=X_{0}X_{n-1}···X_{2}X_{1}$碟式函数（$\beta$）：把输入端的二进制编号的最高位与最低位互换位置得到输出端的编号。
- 第k个子函数：
$\beta_{(k)}(X_{n-1}X_{n-2}···X_{k}X_{k-1}X_{k-2}···X_{1}X_{0})=X_{n-1}X_{n-2}···X_{k}X_{0}X_{k-2}···X_{1}X_{k-1}$ - 第k个超函数：
$\beta^{(k)}(X_{n-1}X_{n-2}···X_{n-k+1}X_{n-k}X_{n-k-1}···X_{1}X_{0})=X_{n-k}X_{n-2}···X_{n-k+1}X_{n-1}X_{n-k-1}···X_{1}X_{0}$ - 碟式变换与交换变换的多级组合是构成多级立方体网络的基础
- 第k个子函数：
反位序函数：将输入端二进制编号的位序颠倒过来求得相应输出端的编号
$\rho(X_{n-1}X_{n-2}···X_{1}X_{0})=X_{0}X_{1}···X_{n-2}X_{n-1}$- 第k个子函数
$\rho_{(k)}(X_{n-1}X_{n-2}···X_{k}X_{k-1}X_{k-2}···X_{1}X_{0})=X_{n-1}X_{n-2}···X_{k}X_{0}X_{1}···X_{k-2}X_{k-1}$ - 第k个超函数
$\rho^{(k)}(X_{n-1}X_{n-2}···X_{n-k+1}X_{n-k}X_{n-k-1}···X_{1}X_{0})=X_{n-k}X_{n-k+1}···X_{n-2}X_{n-1}X_{n-k-1}···X_{1}X_{0}$
- 第k个子函数
移数函数：将各输入端都错开一定的位置（模N）后连到输出端
PM2I函数（加减2^i^函数）
- P和M分别表示加和减，2I表示2^i^
- 一种移数函数
$PM2_{+i}(x)=x+2^i\quad mod(N)$
$PM2_{-i}(x)=x-2^i\quad mod(N)$
$0\leq x\leq N-1\quad o\leq i\leq n-1\quad n=log_2N,N表示结点数$ - PM2I互连网络共有2n个互连函数
静态互连网络
各结点之间有固定的连接通路、且在运行中不能改变的网络。
1、2维互连函数
线性阵列
一种一维的线性网络，其中N个结点由N-1个链路连成一行。
- 端结点的度：1
- 其余结点的度：2
- 直径：N-1
- 等分宽度b=1
环和带弦环
环：线性阵列的两个端点连接起来。可以单向工作也可以双向工作。
- 对称
- 结点的度：2
- 双向环的直径：N/2
- 单向环的直径：N-1
- 环的等分宽度b=2
带弦环
增加的链路越多，结点度越高，网络直径越小
全连接网络：两两结点之间都有链路
循环移数网络：通过在环上每个结点到所有与其距离为2的整数幂的结点之间都增加一条附加链
树形和星形：
树形是二叉树- 最大结点度：3
- 直径：2(k-1)【k层完全平衡的二叉树】
- 等分宽度b=1
星形：
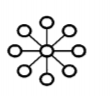
- 结点度：N-1
- 直径较小：2
- 等分宽度b=[N/2]【向下取整】
胖树形
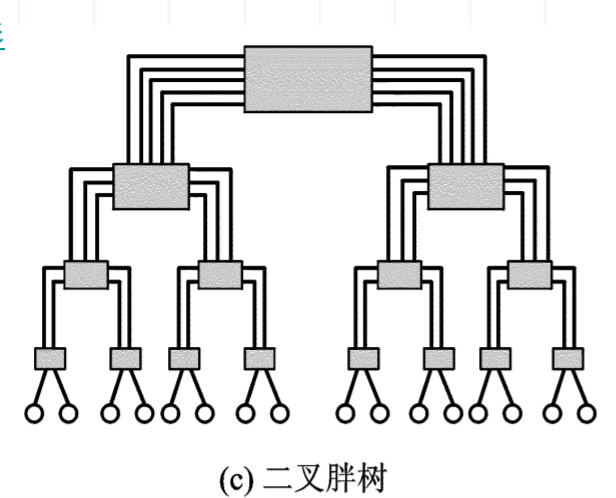
网格形和环网形
- 网格形：
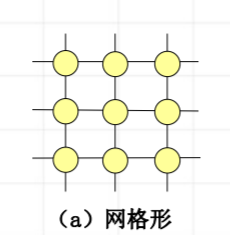一个由N=n^k^个结点构成的k维网格形网络（每维n个结点）的内部结点度d=2k，网络直径D=k(n-1) - Illiac网络：把2维网格形网络的每一列的两个端结点连接起来，再把每一行的尾结点与下一行的头结点连接起来，并把最后一行的尾结点与第一行的头结点连接起来
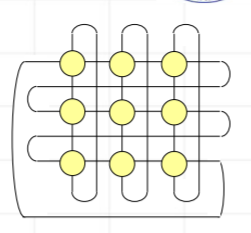一个规模为nxn的Illiac网格：
- 所有结点的度d=4
- 网络直径D=n-1
- 等分宽度：2n - 环网形：把2维网格形网络的每一列的两个端结点连接起来，再把每一行的两个端结点连接起来。
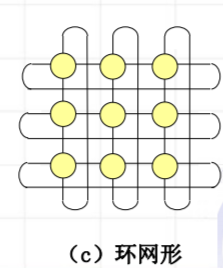一个nxn的环网形网
- 结点度：4
- 网络直径：2x[n/2]【向下取整】
- 等分宽度b=2n
- 网格形：
超立方体和寻径
超立方体
一种二元n-立方体结构，由N=2^n^个结点组成；分布在n维上，每维有两个结点。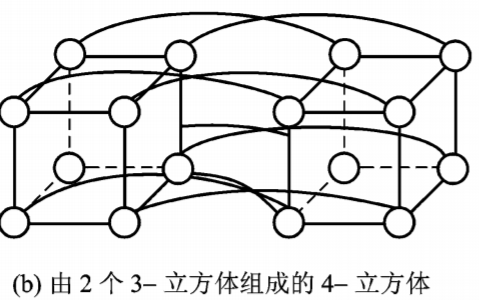
为实现一个n-立方体，只要把两个（n-1）立方体中相对应的结点用链路连接起来即可。共需要2^n-1^条链路。
n-立方体中结点的度都是n，直径也是n，等分宽度为b=N/2。
带环立方体（3-CCC）
将k-立方体的每个结点用由k个结点的环来代替，组成带环k-立方体。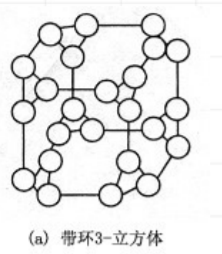
- 网络规模：$N=k\times2^k$
- 网络直径：$D=2k-1+\lfloor k/2\rfloor$
- 等分宽度：$b=\frac{N}{2k}$
k元n-立方体网络
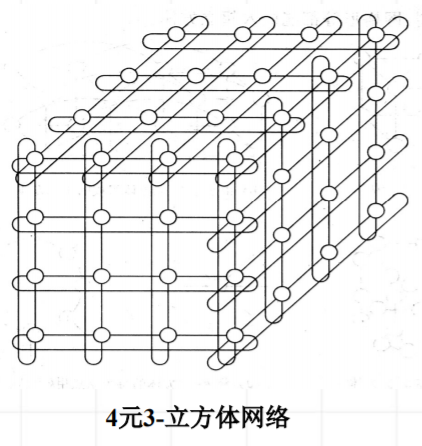
- 环形、网格、环网形、二元n-立方体（超立方体）都是k元n-立方体网络系列的拓扑同构体
- 在k元n-立方体网络中，参数n是立方体的维数，k是基数，即每一维上的结点个数$N=N^n$
- k元n-立方体的结点可以用基数为k的n位地址A=a
1a2a3a4来表示【ai表示该结点在第i维上的位置】 - 通常把低维k元n-立方体称为环网，而把高维k元n-立方体称为超立方体
基于静态互连网络的寻径机制
- 确定性寻径：通信路径完全由源结点地址和目的地址来决定，寻径路径是预先唯一确定好了的，与网络状况无关
- 自适应寻径：通信的通路每一次都要根据资源或者网络的情况来选择【TCP/IP网络】
二维网格网络的X-Y寻径
先沿X维方向进行寻径，然后再沿Y维方向寻找路径
超立方体E-cube寻径
动态互连网络
由交换开关构成、可按运行程序的要求动态地改变连接状态的网络。
总线和交叉开关
总线网络
由一组导线和插座构成，经常被用来实现计算机系统中处理机模块、存储模块和外围设备等之间的互连。