关系模型概述
关系数据理论是建立在集合代数理论基础上的,有着坚实的数学基础
- 数据结构:二维表
- 关系操作:
- 增加(insert)、删除(delete)、修改(updated)
- 查询(Query):•选择(select)、投影(project)、连接(join)
- 除(divide)、并(union)、交(intersection)
- 差(difference)
- 关系代数,关系演算,SQL
- 关系的三类完整性约束:
- 实体完整性、参照完整性、用户自定义的完整性
关系代数是用对关系的运算来表达查询要求的方式。
关系演算是用谓词表达查询要求的方式。
- 按谓词变元的基本对象是元组变量还是域变量分为元组关系演算和域关系演算
关系数据结构
域
- 域是一组具有相同数据类型的值的集合
笛卡儿积
一组域D
1, D2,…, Dn的笛卡尔积为:D1×D2×…×Dn= {(d1, d2, … , dn) | di∈Di, i=1,…,n}笛卡尔积的每个元素(d
1, d2, … , dn)称作一个n-元组(n-tuple)元组的每一个值d
i叫做一个分量(Component)若D
i的基数(元组个数)为mi,则笛卡尔积的基数为
$$
\prod^n_{i=1}m_i
$$一个域允许的不同取值个数称为这个域的基数
笛卡儿积可以表示成一张二维表。表中的每行对应一个元组,表中的每一列的值来自一个域。
关系
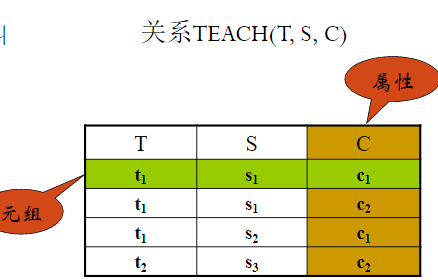
笛卡尔积D
1×D2×…×Dn的子集叫做在域D1, D2,…, Dn上的关系,用R(D1, D2,…, Dn)表示R是关系的名字,n是关系的度或目
当n=1时,称该关系为单元关系
关系是笛卡尔积中有意义的子集,关系中的每个元素是关系中的元组
一般来说,笛卡儿积是没有实际语义的,只有它的某个真子集才有实际含义
关系也可以表示为二维表
属性
- 关系中不同列可以对应相同的域,为了加以区分,必须对每列起一个名字,称为属性
- n目关系必有n个属性
关系数据结构
关系的性质
- 列是同质的;即每一列中的分量是同一类型的数据,来自同一个域。
- 行列的顺序无关紧要;行列的次序是可以任意交换的
- 任意两个元组不能完全相同
- 每一分量必须是不可再分的数据
- 不同的属性,属性名不能相同
候选码(Candidate Key)
- 关系中的一个属性组,其值能唯一标识一个元组。若从属性组中去掉任何一个属性,它就不具有这一性质了,这样的属性组称作候选码如DEPT中的D#,DN都可作为候选码
- 任何一个候选码中的属性称作主属性如SC中的S#,C#
主码(Primary Key)
- 若一个关系有多个候选码,则选定其中一个作为主码如可选定D#作为DEPT的主码
外码(Foreign Key)
- 关系R中的一个属性组,它不是R的码,但它与另一个关系S的码相对应,则称这个属性组为R的外码
如S关系中的D#属性
关系模式
形式化的表示为R(U,D,DOM,F)
R为关系名,U为组成该关系的属性名集合;D为U中属性所来自的域;DOM为属性向域的映象集合;F为属性间数据的依赖关系集合。
- 关系的描述称作关系模式,包括关系名、关系中的属性名、属性向域的映象、属性间的数据依赖关系等,记作R(A
1, A2,…, An) - 属性向域的映象一般直接说明为属性的类型、长度等
- 某一时刻对应某个关系模式的内容(元组的集合)称作关系
- 关系模式是型,是稳定的
关系是某一时刻的值,是随时间不断变化的
关系数据库
其型是关系模式的集合,即数据库描述,称作数据库的内涵(Intension),或关系数据库模式
其值是某一时刻关系的集合,称作数据库的外延(Extension),或关系数据库
关系的完整性约束
实体完整性
- 关系的主码中的属性值不能为空值
- 空值:不知道或无意义
- 意义:关系对应到现实世界中的实体集,元组对应到实体,实体是相互可区分的,通过主码来唯一标识,若主码为空,则出现不可标识的实体,这是不容许的
参照完整性
- 如果关系R
2的外码Fk与关系R1的主码Pk相对应,则R2中的每一个元组的Fk值或者等于R1中某个元组的Pk值,或者为空值【即属性Fk本身不是主属性,则可以取空值,否则不能取空值。】 - 意义:如果关系R
2的某个元组t2参照了关系R1的某个元组t1,则t1必须存在 - 例如:关系S在D#上的取值有两种可能
- 空值,表示该学生尚未分到任何系中
- 若非空值,则必须是DEPT关系中某个元组的D#值,表示该学生不可能分到一个不存在的系中
DEPT(D#, DN , DEAN)S(S#, SN , SEX , AGE , D#)
用户定义的完整性
用户定义的完整性
用户针对具体的应用环境定义的完整性约束条件
如S#要求是8位整数,SEX要求取值为“男”或“女”
系统支持
- 实体完整性和参照完整性由系统自动支持
- 系统应提供定义和检验用户定义的完整性的机制
关系代数概述
- 属于关系操作的一种
- 关系代数是一种抽象的查询语言
- 通过对关系的运算来表达查询操作
- 运算对象、结果均为关系
- 运算包括四类:
- 集合运算、关系运算、比较运算、逻辑运算
集合运算
并运算
所有至少出现在两个关系中之一的元组集合
两个关系R和S若进行并运算,则它们必须是相容的:
- 关系R和S必须是同元的,即它们的属性数目必须相同
- 对i,R的第i个属性的域必须和S的第i个属性的域相同
差运算
所有出现在一个关系而不在另一关系中的元组集合
R和S必须是相容的
交运算
- 所有同时出现在两个关系中的元组集合
- 交运算可以通过差运算来重写
基本关系运算
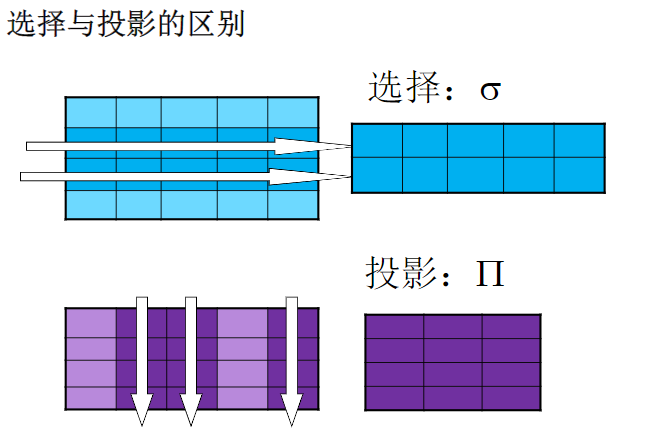
选择运算
在关系R中选择满足给定条件的元组(从行的角度)
投影运算
投影的结果中要去掉相同的行
广义笛卡儿积
元组的连串(Concatenation)
- 若r = (r
1,…,rn),s = (s1,… ,sm),则定义r与s的连串为:rs = (r1,…,rn,s1,…,sm)
- 若r = (r
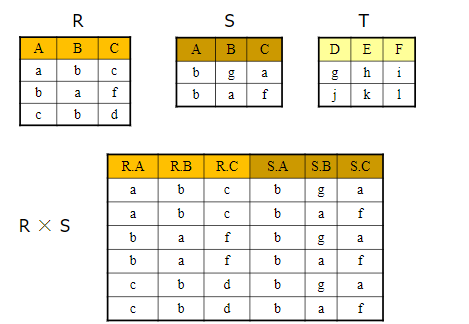
广义笛卡尔积两个关系R,S,其度分别为n,m,则它们的笛卡尔积是所有这样的元组集合:元组的前n个分量是R中的一个元组,后m个分量是S中的一个元组
RxS={rs|r属于R并且s属于S}RxS的度为R与S的度之和,RxS的元组个数为R和S的元组个数的乘积
其它关系运算

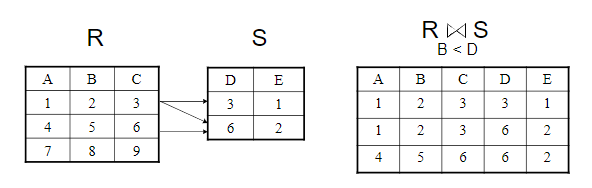
0连接就是有附加条件的自然连接。

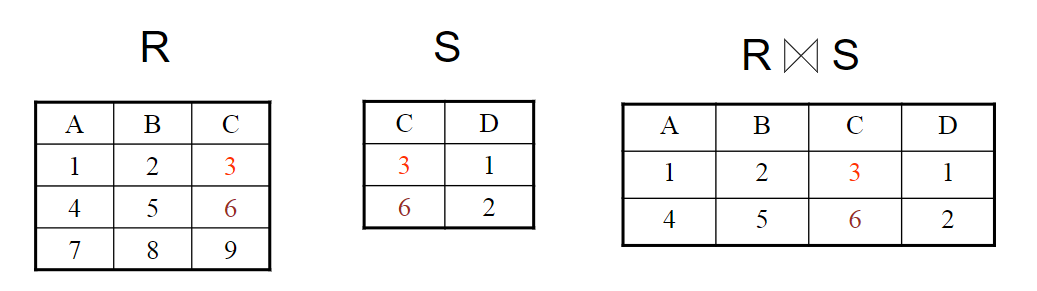
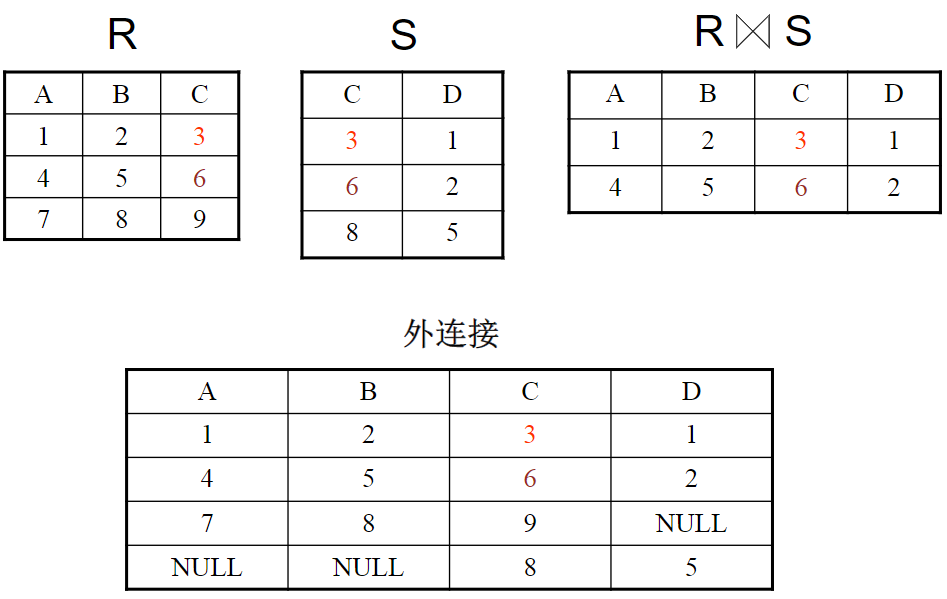
外连接
把上述中舍弃的元组也保存在结果关系中,在其他属性上填上NULL。
左外连接:只把左边关系R中要舍弃的元组保留。同理:右外连接。
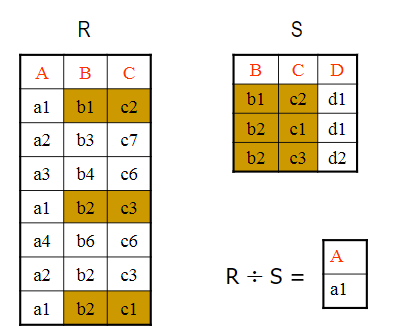
除运算
把S和R中相同的属性组拿出来,然后取R中独有的属性