rhb_blog

rao的博客

0%

编译原理-LR分析

发表于 更新于 分类于 ，

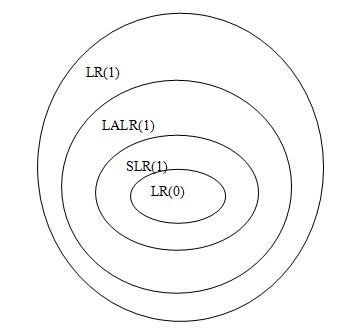
句柄和规范归约

归约：根据文法的产生式规则，把串中出现的产生式的右部替换成左部符号

从语法树的角度看，是从叶子出发逐步向上进行构造

句柄：最左两代子树末端就是句柄

规范归约的关键是寻找句柄：

1、根据语法树找句柄

2、在栈中根据三类信息：

  • 历史：已经移入符号栈的内容
  • 展望：根据产生式推迟未来可能遇到的输入符号
  • 现实：当前的输入符号

LR分析

LR分析法也是一种“移进—归约”的自底向上语法分析方法，其本质是规范归约【句柄作为可归约串】。

其思想为一方面记住已移进和归约出的整个符号串，另一方面根据所用产生式推测未来可能碰到的输入符号。

LR分析方法：把“历史”以及“展望”综合抽象成状态；由栈顶的状态和现行的输入符号唯一确定每一步工作。

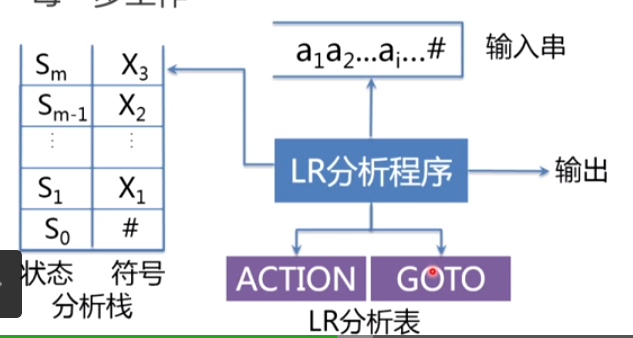
解释：每一个符号对应一个状态，分析栈每次弹出一个符号，就要把对应的状态也弹出。然后LR分析程序会根据输入串在LR分析表中进行查找：是进行归约、移进还是报错操作。

LR分析器实质上是一个带先进后出存储器（栈）的确定有限自动机，其核心部分是一张分析表，包括两部分：

（1）ACTION[s，a]动作表，规定当状态s面临输入符号a时，应采取什么动作（移进、归约、接受、 报错）【也就是告诉我们当栈顶状态为s时，输入的符号是a时，我们应该采取什么操作：归约、移进还是报错】

（2）GOTO[s，X]状态转换表规定了状态s面对文法符号X时，下一状态是什么。【当归约完了后，要把规约后的非终结符压到栈里面的时候，跟新压入栈的这个非终结符所对应的状态是什么】

LR文法

对于一个文法，如果能够构造一张分析表，使得它的每个入口均是唯一确定的，则这个文法就是LR文法

一个文法，如果能用一个每步顶多向前检查k个输入符号的LR分析器分析，则这个文法就称为LR(K)文法

LR文法不是二义的

LR(0)分析

拓广文法

对于文法 G = (VN, VT, P , S ) , 增加如下产生式：S’->S ，其中， S’ ∈ VN∪ VT ， 得到 G 的拓广文法，G’ = (VN ’, VT, P ’ , S’ )

其实就是增加了一条右部为开始符号的产生式，就变成了拓广文法

可归前缀

将符号串的任意含有头符号的子串称为前缀。特别地，空串ε为任意串的前缀。

采取归约过程前符号栈中的内容，称做可归前缀。
这种前缀包含句柄且不包含句柄之后的任何符号；

活前缀

就是在LR分析中为了描述栈内符号的特点给出的概念

对于文法 G = (VN, VT, P , S ) , 设 S’ 是其拓广文法的开始符号（即有产生式 S’-> S）， 且α,β∈(VN∪VT)* , ω∈VT。
若 S’ =^^=>α A ω 且 A ->β， 即 β 为句柄，则 αβ 的任何前缀 γ 都是文法 G 的活前缀。【活前缀就是不含句柄之后任何符号的前缀】
注：由于 S’ =^*^=>S’ 且 S’ -> S， 故 S 是 G 的活前缀 。

也就是说可归前缀的所有前缀（包括可归前缀）都是活前缀。

例：文法 G[S] :
（1） S -> AB
（2） A -> aA
（3） A -> ε
（4） B -> b
（5） B -> bB
句子 aaab 是一个句型，其唯一的句柄为：ε （aaaεb）； 活前缀有：ε，a，aa，aaa。

规范归约过程中，保证分析栈中总是活前缀，就说明分析采取的移进/归约动作是正确的

LR(0)项目

对于文法G，其产生式右部添加一个特殊的符号“.”，就构成文法的一个LR(0)项目，简称项目

每个项目的含义是：欲用改产生式归约时，圆点前面的部分为已经识别了的句柄部分，圆点后面的部分为期望的后缀部分。

分类：

移进项目: 形如 A -> α • aβ（a∈VT），对应移进状态，把a移进符号栈。
待约项目: 形如 A -> α • Bβ，对应待约状态，需要等待分析完非终结符B的串再继续分析A的右部。
归约项目: 形如 A -> α •，句柄已形成，可以归约。
接受项目: 形如 S’ -> S •。【也是一个归约项目，表示整个句子已经识别完毕】
初始项目: 形如 S’ -> • S。
其中a∈VT , α,β∈(VN∪VT)*， A,B∈VT
后继项目: 表示同属于一个产生式的项目，但是圆点的位置仅相差一个文法符号，则称后者为前者的后继项目。

• 的左边是已经归约，右边是没有归约的

例：对于产生式S -> aAcBe，它有6个项目：
S -> ·aAcBe
S -> a·AcBe
S -> aA·cBe
S -> aAc·Be
S -> aAcB·e
S -> aAcBe·

LR(0)有限状态机的构造方法

构造识别活前缀的NFA

NFA的构造方法

(1)状态集：由每个项目所对应的状态组成的集合；

(2)输入字符集合：由文法符号组成，包括：终结符、非终结符和e；

(3)初态：对于文法G[S]的拓广文法G[S’],有项目S’® . S ,由于S’ 仅在第一个产生式的左部出现，所以规定它为初态；

(4)终态：每个状态均为NFA的终态（活前缀的识别态）。

  • 若状态i为X->X1····Xi-1•Xi····Xn；状态j为X->X1····Xi-1Xi•Xi+1····Xn

    则从状态i画一条标志为Xi的有向边到状态j

  • 若状态i为X->α• Aβ，A为非终结符，
    则从状态i画一条ε边到所有状态A->• y【可以理解成X想要把A进行归约，然后画一条ε边，交给A需要归约的符号】

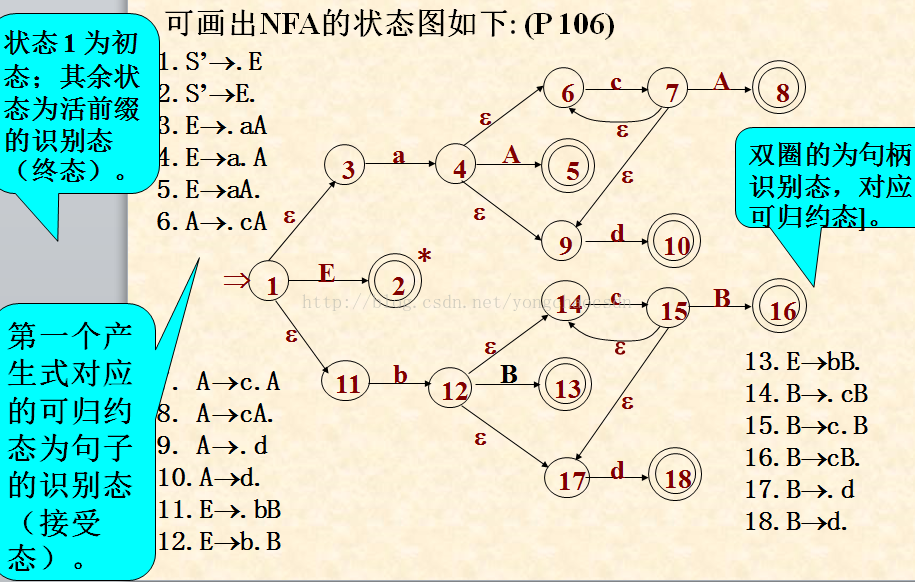
NFA转换成DFA

DFA是用子集法得到的

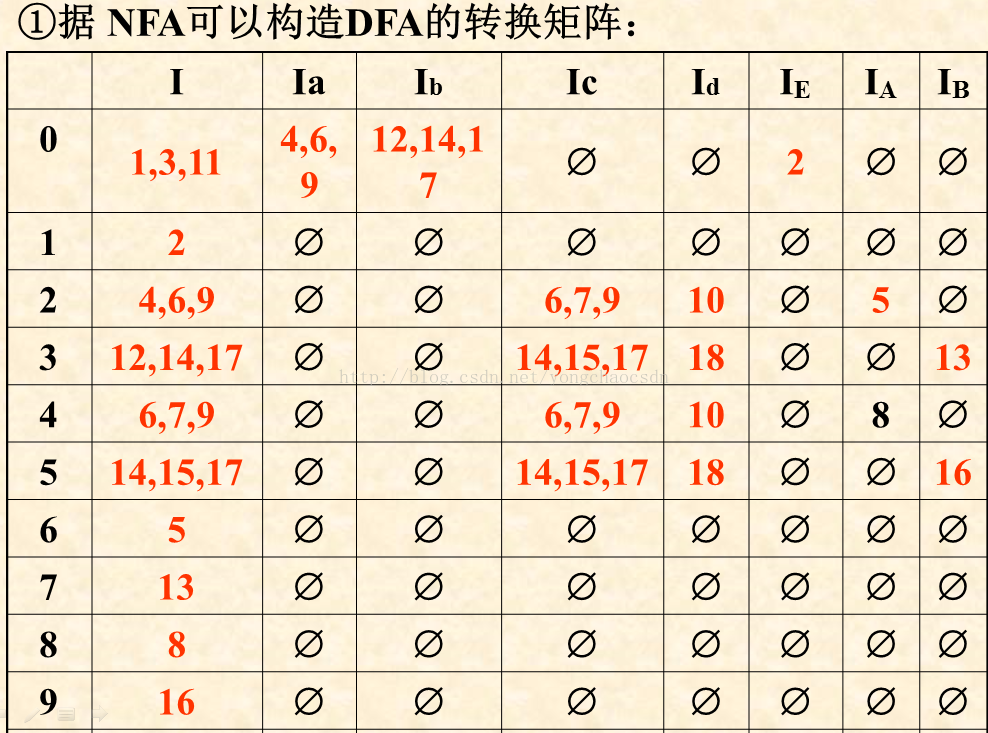
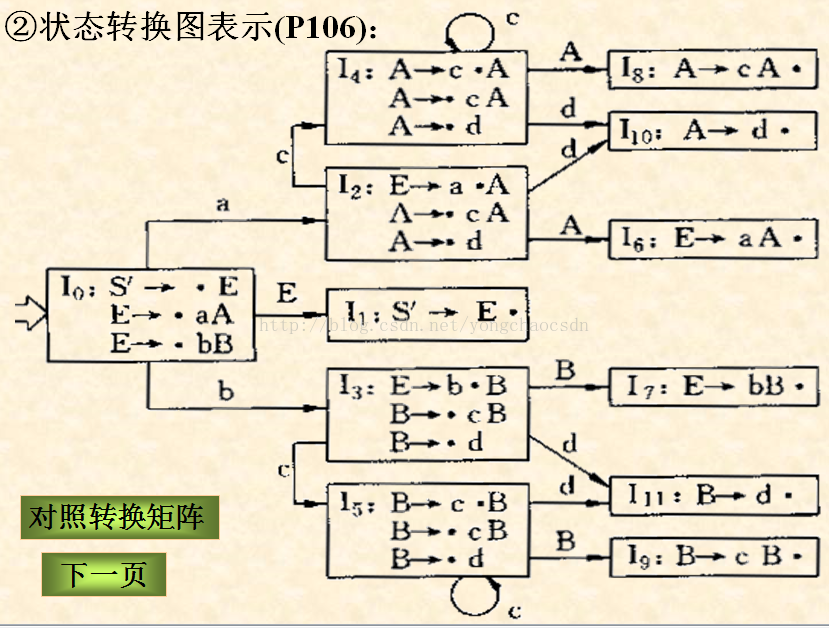
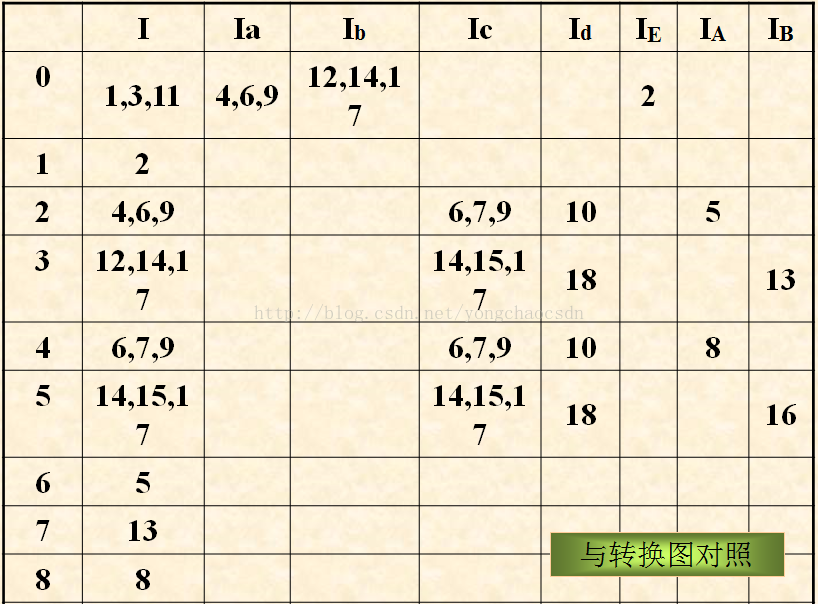
求项目集规范族

每个项目集对应一个DFA状态，它们的全体称为这个文法的项目集规范族

有效项目

项目A->β1• β2对活前缀αβ1是有效的，其条件就是存在规范推导

1.用闭包函数（CLOSURE）来求DFA一个状态的项目集

I是拓广文法G的任意项目集：
CLOSURE(I)是这样定义的：
首先I的项目都属于CLOSURE(I)；
如果A->α• Bβ,则左部为B的每个产生式中的形如B->·γ项目，也属于CLOSURE(I)；

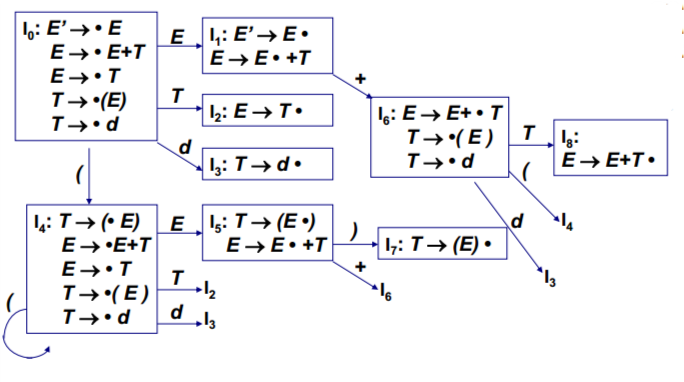
例子：已知文法G[E]如下:
(1) E -> E+T
(2) E -> T
(3) T ->( E )
(4) T -> d

可以直到它的拓广文法G’ [E’]为 ：
(0) E’ -> E
(1) E -> E+T
(2) E -> T
(3) T -> ( E )
(4) T -> d

令I0 = CLOSURE({E’->.E})

则I0 = {
E’ -> • E，
E -> • E+T，
E -> • T，
T -> •( E ),
T -> • d
}

2.LR(0) FSM 的状态转移函数

从一个状态出发，到达下一个状态的转换函数：
GO (I,X) = CLOSURE(J)
其中，I为LR(0) FSM 的状态（闭包的项目集），X为文法符号， J={ A -> αX•β | A -> α• Xβ∈I} ；【J是非终结符包进去后的集合】
表示对于一个状态项目集中的一个项目A -> α• Xβ，在下一个输入字符是X的情况下，一定到另一个新状态 A -> αX•β。

3.LR(0) 有限状态机的构造

从 LR(0) FSM 的初态出发 ，先求出初态项目集的闭包（CLOSURE({S’->.S})），然后应用上述转移函数，通过项目分析每种输入字符下的状态转移，若为新状态，则就求出新状态下的项目集的闭包，级可逐步构造出完整的 LR(0) FSM。

1
2
3
4
5
6
7
8
9
10
构造项目集规范族的算法：
PROCEDURE ITEMSET(G')；
BEGIN
C:{CLOSURE{S'->.S}};
	REPEAT
	FOR C中的每一个项目集I和G'的每一个符号X DO
		IF GO(I,X)非空且不属于C THEN
		把GO(I,X)放入C族中
	UNTIL C不再增大
End

LR(0) FSM 的构造举例
给定文法G[E]：
(1) E -> E+T
(2) E -> T
(3) T -> ( E )
(4) T -> d

构造LR(0) FSM
① G[E]的拓广文法，得到G’ [E’]：
(0) E’ -> E
(1) E -> E+T
(2) E -> T
(3) T -> ( E )
(4) T -> d

②构造G’[E’] 的 LR(0) FSM

两种构造识别活前缀的DFA的方法：

  • 项目->NFA->DFA
  • Closure->GO->DFA

LR(0) 分析法

1.LR(0) 文法定义

文法 G 是 LR(0) 文法，当且仅当它的LR(0)FSM中的每个状态都满足：
①不同时含有移进项目和归约项目，即不存在移进-归约冲突。
②不含有两个以上归约项目，即不存在归约-归约冲突。

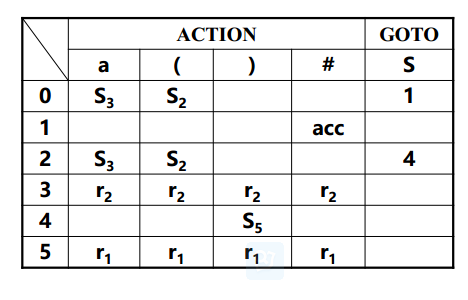
2.LR(0)分析表的构造

令每个项目集Ik的下标k作为分析器的状态

ACTION 表项和 GOTO表项可按如下方法构造：

  • 若项目A ->α • aβ属于 Ik 且 GO (Ik, a)= Ij, 期望字符a 为终结符，则置ACTION[k, a] =sj (j表示新状态Ij);

  • 若项目A ->α •属于Ik, 那么对任何终结符a, 置ACTION[k, a]=rj；其中，假定A->α为文法G 的第j个产生式；【对k到a进行归约】

  • 若项目S’ ->S • 属于Ik, 则置ACTION[k, #]为“acc”;【单词处理完毕】

  • 若项目A ->α • Aβ属于 Ik，且GO (Ik, A)= Ij,期望字符 A为非终结符，则置GOTO(k, A)=j (j表示文法中第j个产生式);

  • 分析表中凡不能用上述规则填入信息的空白格均置上“出错标志”

    翻译一下：

    1. 如果圆点不在项目k最后且圆点后的期待字符a为终结符，则ACTION[k, a] =sj (j表示新状态Ij)；
    2. 如果圆点不在项目k最后且圆点后的期待字符A为非终结符，则GOTO(k, A)=j (j表示文法中第j个产生式)；
    3. 如果圆点在项目k最后且k不是S’ ->S，那么对所有终结符a，ACTION[k, a]=rj (j表示文法中第j个产生式)；
    4. 如果圆点在项目k最后且k是S’ ->S，则ACTION[k, #]为“acc”;

例子：

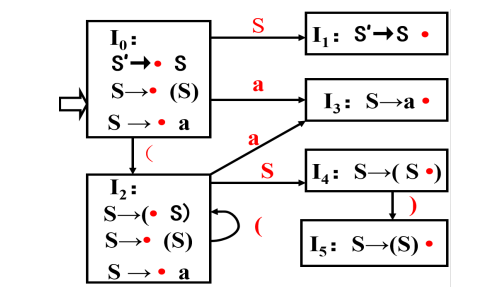
考虑文法G[S] :
S → （S） | a
相应的LR(0) FSM如下，构造其LR(0)分析表。

LR(0) FSM

从I0看，S‘->·S,期望字符是非终结符S，根据上面的规则2，得到GOTO(0,S)=1；
S‘->·(S),期望字符是终结符(，根据上面的规则1，得到ACTION(0,()=S2；
从I3看，S->a·，根据规则3，置ACTION[3, a]为r2;
从I1看，S‘->S·，根据规则4，置ACTION[1, #]为“acc”;

LR(0)分析表

3.LR(0) 分析流程

设输入串为w，ip指向输入串w的首符号a，i指向符号栈顶；状态栈的初始栈顶为0，符号栈初始栈顶为#。

算法流程图为：

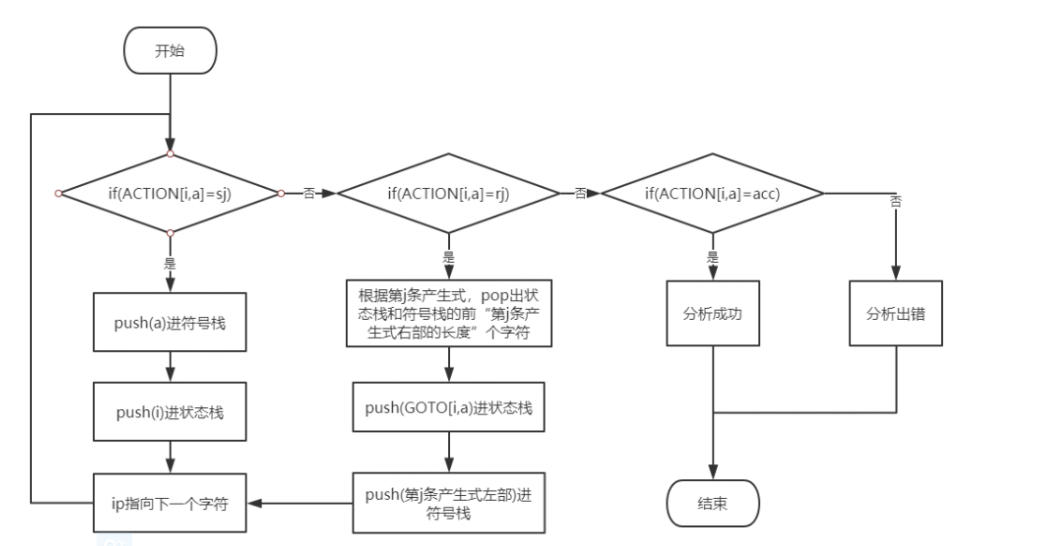
SLR(1)分析法

1.SLR(1)解决的问题

LR(0)文法的要求是①不同时含有移进项目和归约项目，即不存在移进-归约冲突。②不含有两个以上归约项目，即不存在归约-归约冲突。

例如项目集Ii中存在： Ii ＝{A->α•bγ ， B→ γ•，C→β• }，此时就同时存在移进-归约冲突和归约-归约；因为你不知道下一步是选择归约还是移进，选择归约的话选择哪个产生式归约。

而事实上一般文法满足这种要求有一定难度，但是假如在归约时出现了移进-归约冲突或者归约-归约冲突，我们可以通过在待分析的字符串中向后再看一位，大多数情况下通过这一位字符就可以确定，选择哪一个表达式归约，或是移进操作。

这种方法就叫做SLR(1)分析法，即简单的LR(1)分析法。

2.SLR(1)冲突解决方法

如上面所述，我们需要知道下一位待分析的字符，然后和现有项目进行比较。

分析过程与LR(0)一样，但是需要解决分析表上的冲突问题。

假如LR(0) 项目集规范族中有项目集 Ii 含有移进-归约冲突和归约-归约冲突：
Ii ＝{A1->α1•b1γ1，… ， Am->m•bm γm， B1->β1• ，…， Bn-> βn• }，若集合{b1 ，b2，… ，bm }、FOLLOW(B1) 、 FOLLOW(B2) ，…，FOLLOW(Bn)均两两不相交，则可用SLR(1)解决方法解决分析表上第i行上的冲突问题。

假设下一个移进的字符为b:

1、若b∈ {b1 ，b2，… ，bm }，则移进输入符；

2、若b∈FOLLOW(Bj) ，j＝1 ，… ，n，则用Bj-> βj 归约；

3、此外，报错

通过这个方法，就可以在知道下一位待分析的字符的情况下，解决冲突。

继续采用SLR(1)分析的方法，我们可以对出错情况进行优化：

在LR(0)和SLR(1)分析中，我们在可以归约且没有冲突时（假如归约成A），是不关心下一位待分析的字符a和follow(A)的关系的，假如a!∈follow(A)则当前字符串是不被接受的，当然这会在之后的继续移进字符过程中发现错误，但是如果不管是否有冲突看，将SLR(1)分析方法应用到所有分析表的构建过程中，可以提前发现字符串的错误。

3.构造SLR(1)分析表的方法

1、把G扩广成G’

2、对G’构造：得到LR(0)项目集规范族C；活前缀识别自动机的状态转换函数GO

3、使用C和GO，构造SLR分析表：构造action和goto子表：

  • 若项目A ->α • aβ属于 Ik 且 GO (Ik, a)= Ij,期望字符a为终结符，则置ACTION[k, a] =sj (j表示新状态Ij);
  • 若项目A ->α • Aβ属于 Ik，且GO (Ik, A)= Ij,期望字符 A为非终结符，则置GOTO(k, A)=j (j表示文法中第j个产生式);
  • 若项目A ->α •属于Ik, 那么对任何终结符a，当满足a属于follow(A)时， 置ACTION[k, a]=rj；其中，假定A->α为文法G 的第j个产生式；
  • 若项目S’ ->S • 属于Ik, 则置ACTION[k, #]=“acc”;
  • 分析表中凡不能用上述规则填入信息的空白格均置上“出错标志”

SLR分析是有选择的放置的

4.SLR（1）文法

按上述方法构造出的ACTION和GOTO表如果不含多重入口，则称该文法是SLR(1)文法。

使用SLR表的分析器叫做一个SLR分析器

每个SLR(1)文法都是无二义的。
$$
LR(0)\subset SLR(1)\subset 无二义文法
$$

5.SLR(1)分析的例子

算术表达式文法G[E]：
E→E +T | T
T→T * F | F
F→ （E）| i
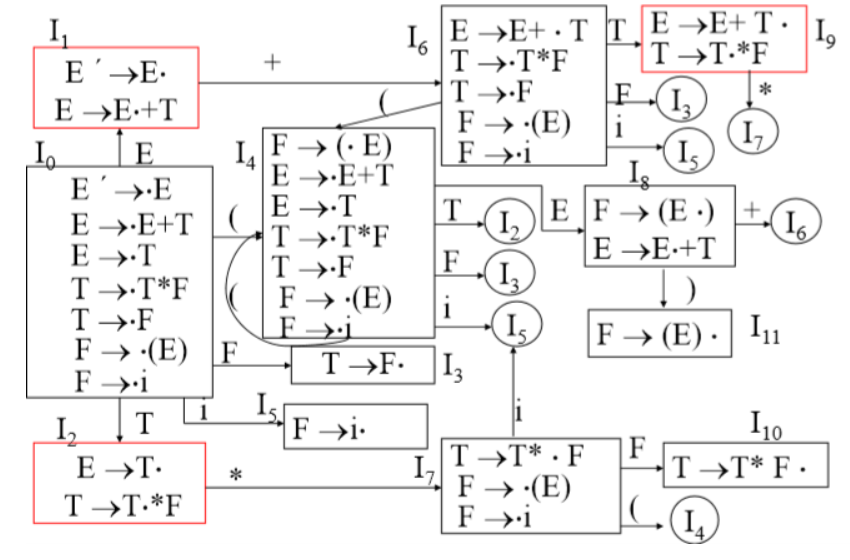
求此文法的识别规范句型活前缀的DFA，分析句子i+i *i。

  1. 将文法拓广为G’[E’]：
    (0) E’ ->E
    (1) E-> E +T
    (2) E ->T
    (3) T ->T * F
    (4) T ->F
    (5) F ->(E)
    (6) F ->i
  2. 构造识别规范句型活前缀的DFA

  1. 判断有无冲突：

    I1 ，I2 ，I9有移进_归约冲突。
    I1:E´ ->E· E ->E·+T
    I2: E ->T · T ->T · *F
    I9: E ->E+T· T ->T · *F

  2. 考虑能否用SLR(1)方法解决冲突：

    对于I1: { E´ ->E· E ->E·+T} 因为：{+} ∈FOLLOW(E´)= {+} ∩ {＃} ＝∅, 所以可用SLR(1)方法 解决I1的冲突。

    对于I2: {E ->T· T ->T·*F} 因为：{*} ∈ FOLLOW(E)= {*} ∩ {＃，）,+} ＝ ∅ 所以可用SLR(1)方法解决I2的冲突。

    对于I9: {E ->E+T· T ->T ·*F} 因为：{*} FOLLOW(E)= ∅, 所以可用SLR(1)方法解决I9的冲突。

  3. 构建分析表：

6.句子i+i *i的分析过程：

步骤 状态栈 符号栈 输入符 剩余输 入串 查表 操作
1 0 # i i+i*i# Action[0,i]=S5 移进i
2 0 5 # i + +i*i# Action[5,+]=r6,GOTO(0,F)=3 用F -> i 归约
3 0 3 # F + +i*i# Action[3,+]=r4,GOTO(0,T)=2 用F -> T归约
4 0 2 # T + +i*i# Action[2,+]=r4,GOTO(0,E)=1 用F -> E归约
5 0 1 # E + +i*i# Action[1,+]=S6 移进+
6 0 1 6 # E + i i*i# Action[6,i]=S6 移进+
7 0 1 6 5 # E + i * *i# Action[5,*]=r6,GOTO(6,F)=3 用F -> i 归约
8 0 1 6 3 # E + F * *i# Action[3,*]=r6,GOTO(6,T)=9 用F -> F 归约
9 0 1 6 9 # E + T * *i# Action[9,*]=S7 移进*
10 0 1 6 9 7 # E + T * i i# Action[7,i]=S5 移进i
11 0 1 6 9 7 5 # E + T * i # # Action[5,#]=r6,GOTO(7,F)=10 用F -> i 归约
12 0 1 6 9 7 10 # E + T * F # # Action[10,#]=r3,GOTO(6,T)=9 用T -> T+F归约
13 0 1 6 9 # E + T # # Action[9,#]=r1,GOTO(0,E)=1 用E -> E+T归约
14 0 1 # E # # Action[1,#]=acc 接受

LR(1)分析法

SLR冲突消解存在的问题

在SLR方法中，如果项目集Ii含项目A ->α •而且下一输入符号α∈FOLLOW(A)，则状态i面临α时，可选用“用A ->α归约”动作。

但是在某些情况下，当状态i显现于栈顶时，当前单词是α，栈里的活前缀βα未必允许把α归约为A，因为可能根本不存在一个形如“βAα”的规范句型。在这种情况下，用“A ->α”归约不一定合适

【因为FOLLOW（A）集合提供的信息太泛】

构造LR(1)分析表的方法

1、把G扩广成G’

2、对G’构造：得到LR(1)项目集规范族C；活前缀识别自动机的状态转换函数GO

3、使用C和GO，构造LR（1）分析表：

LR(K)项目：扩展LR(0)项目，附带有k个终结符[A->α •β,α1α2····αk]
α1α2····αk称为向前搜索符串（或展望串）

归约项目[A->α •,α1α2····αk]的意义：当它所属的状态呈现现在栈顶且后续的k个输入符号为α1α2····αk时，才可以把栈顶上的α归约为A

对于任何移进或待约项目[A->α •β,α1α2····αk]，β不等于α，搜索符串α1α2····αk没有直接作用 

1
2
3
4
5
6
7
8
9
10
构造项目集规范族的算法：
PROCEDURE ITEMSET(G')；
BEGIN
C:{CLOSURE{S'->.S,#}};
	REPEAT
	FOR C中的每一个项目集I和G'的每一个符号X DO
		IF GO(I,X)非空且不属于C THEN
		把GO(I,X)放入C族中
	UNTIL C不再增大
End
  • 若项目[A ->α • aβ，b]属于 Ik 且 GO (Ik, a)= Ij,期望字符a为终结符，则置ACTION[k, a] =sj (j表示新状态Ij);
  • 若项目[A ->α •，a]属于Ik, 那么对任何终结符a，当满足a属于follow(A)时， 置ACTION[k, a]=rj；其中，假定A->α为文法G 的第j个产生式；
  • 若项目[S’ ->S • ，#]属于Ik, 则置ACTION[k, #]=“acc”;
  • 若GO[Ik，A]=Ij，则置GOTO[K,A]=j
  • 分析表中凡不能用上述规则填入信息的空白格均置上“出错标志”

$$
LR(0)\subset SLR(1)\subset LR(1)\subset 无二义文法
$$

（SLR(1)和LR(1)的区别在于LR(1)多使用了一个预判信息，即项目后面的符号如A →·e,c中的c，这个预判信息是用first集而非follow集得出的）

LR(0)、SLR(1)、LL(1)等的区别

LL(1)定义：一个文法G是LL（1）的，当且仅当对于G的每一个非终结符A的任何两个不同产生式 A→α|β，下面的条件成立：SELECT( A→α)∩SELECT( A→β)=,其中，

α|β不能同时ε。

解释：LL(1)的意思是，第一个L,指的是从左往右处理输入，第二个L,指的是它为输入生成一个最左推导。1指的是向前展望1个符号。LL(1)文法是上下文无关文法的一个子集。它用的方法是自顶向下的(递归式的处理)。它要求生成的预测分析表的每一个项目至多只能有一个生成式。上面的定义说的是，任何两个不同的产生式 A→α和 A→β,选择A→α或者 A→β是不能有冲突的，即SELECT( A→α)∩SELECT( A→β)=，具体来说，就是，第一:First( A→α) ∩ First( A→β)=,首符集不能有交集，否则当交集中的元素出现时，选择哪个产生式进行推导是不确定的，（这其中也包含了α|β不能同时ε，否则交集就是{ε}不为空），第二：若任何一个产生式β，有ε属于First(β),应有First(A)∩Follow( A)为空（当ε属于First(β)，则A有可能被空串代替，那么就要看A的下一个字符，即Follow集，即要求Follow集和First集不能相交，否则可能发生冲突）。

LR文法：定义：如果某一文法能够构造一张分析表，使得表中每一个元素至多只有一种明确动作，则该文法称为LR文法。

拓展：由上面的定义可以看到，LL(1)和LR文法都是无二义性的：LL(1)要求生成的预测分析表的每一个项目至多只能有一个生成式，即对于读头下的每一个字符，都可以明确地选择哪个产生式来推导，LR文法要求每一步都有明确的动作，移进和归约都是可确定的，没有二义性。

比较两大类型（自顶向下　vs 自底向上）的文法的特点：

1.首先LL(1)分析法是自上而下的分析法。LR(0),LR(1),SLR(1),LALR(1)是自下而上的分析法。
2.自上而下:从开始符号出发，根据产生式规则推导给定的句子。用的是推导
3.自下而上:从给定的句子规约到文法的开始符号。用的是归约
4.自上而下就是一种试探过程，怎么试探？需要你写出它的FIRST()集与FOLLOW()集。写出这两个集合后根据LL(1)分析表构造规则画出LL(1)分析表。现在基本完成了大半，当计算机输入句子时，分析程序便会根据输入去和分析表进行匹配，如果每步都能够匹配成功则说明符合该语法规则，分析成功。
FIRST()集：其实是终结符的集合，看该非终结符A能不能产生以它里面的某个符号开头的句子。（这也是自上而下分析法的思想）
5.自下而上就是把句子变成非终结符，在把非终结符变成非终结符，这样不断的进行如果能到根节点则成功。

LL(1)就是向前只搜索1个符号，即与FIRST()匹配，如果FIRST为空则还要考虑Follow。
　 LR需要构造一张LR分析表，此表用于当面临输入字符时，将它移进，规约（即自下而上分析思想），接受还是出错。
LR(0)找出句柄前缀，构造分析表，然后根据输入符号进行规约。不考虑先行，只要出现终结符就移进，只要出现归约状态，就无条件归约,这样子可能出现归约－移进，归约－归约冲突。
SLR(1)使用LR(0)时若有归约－归约冲突，归约－移进冲突，所以需要看先行，则只把有问题的地方向前搜索一次。

SLR(1)定义：满足下面两个条件的文法是SLR(1)文法

a.对于在s中的任何项目 A→α.Xβ,当X是一个终结符，且X在Follow(B)中时，s中没有完整的项目B→r.

b.对于在s中的任何两个完整项目A→α.和 B→β.,Follow(A)∩Follow(B)为空。

解释：a.当X是一个终结符且X出现在读头上，对于项目 A→α.Xβ应该采用移进，若有完整的项目B→r.且Follow(B)中有X，当X出现在读头上时，此时应该归约，于是，就产生了移进和归约冲突

b.假设Follow(A)∩Follow(B)为{ X },对于A→α.，若Follow(A)[A后面的元素]出现时，应该归约，同理B也一样，于是，会产生归约－归约冲突，SLR(1)是为了消除LR(0)的两个冲突。
LR(1)1.在每个项目中增加搜索符。2.举个列子如有A->α.Bβ，则还需将B的规则也加入。
LALR(1)就是假如两个产生式集相同则将它们合并为一个，几合并同心集

总结：

见到First集就移进，见到Follow集就归约。

LR(0):见到First集就移进，见到终态就归约

SLR(1)见到First集就移进，见到终态先看Follow集，与Follow集对应的项目归约，其它报错。

SLR分析法包含的展望信息是体现在利用了Follow(A)信息，可以解决“归约－归约”冲突

SLR分析法没有包含足够的展望信息，不能完成解决“移进－归约”冲突，需要改进。

下面是LR(0),SLR(1),LALR(1),LR(1)文法处理能力的比较，圆圈越大说明能力越强。