词法分析程序设计
词法分析任务
词法分析阶段是编译的第一阶段,它的主要任务是从左至右扫描文本格式的源程序,从基于字符理解的源程序中分离出符合源语言词法的单词,最终转换成基于单词理解的源程序。
输出形式为: (单词种类,单词)
单词种类类似于自然语言的词性,由构词规则等因素确定的。
计算机高级语言一般都有关键字、标识符、常数、运算符和定界符这5类单词。
词法分析程序和语法分析程序的接口方式
词法分析程序通常与后阶段语法分析程序接口有下列两种方式。
⑴词法分析程序和语法分析程序各自独立一趟方式。即词法分析程序把字符流的源程序转换成单词流的内部程序形式,供语法分析程序之用。
⑵词法分析程序和语法分析程序合并为一趟方式。即词法分析程序由反复语法分析程序调用,每调用一次从源程序中一个新单词返回给语法分析程序。
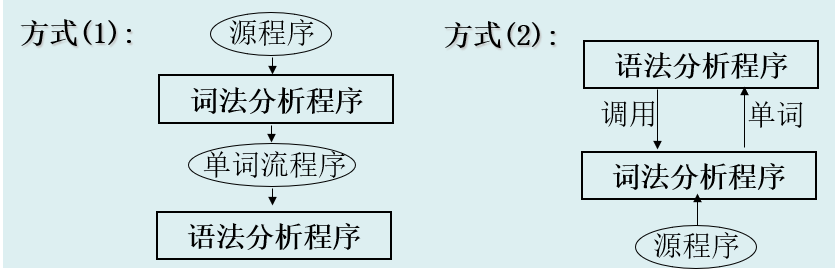
第一种方式的效率比较低。
单词的描述工具
基于生成观点、计算观点和识别观点,分别形成了正规文法、正规式和有穷自动机 3种用于描述计算机高级语言词法的工具。
正规文法
对应的是生成观点。
左线性/右线性正规文法描述。

正规式
对应的是计算观点。
基于字母表∑上的正规式(也称为正则表达式)定义如下,正规式e的计算值称为正规集,记为L(e)。
ε是∑上的正规式,L(ε)= {ε} 【ε是空串】
Ф是∑上的正规式,L(Ф)=Ф【Ф和ε不一样,它表示的是空集,对应的是实体的完整性】
任何a∈∑,a是∑上的正规式,L(a)= {a}
如果e
1和e2是∑上的正规式,则4.1. (e
1)是∑上的正规式,L((e1))=L(e1)【直接脱括号】4.2. e
1︱e2是∑上的正规式,L(e1︱e2)=L(e1)∪L(e2)4.3. e
1· e2是∑上的正规式,L(e1· e2)=L(e1)·L(e2)4.4. e
1* 是∑上的正规式,L(e1*)=L(e1)* 【闭包运算】
字母表∑1和∑2的乘积( product):
∑1∑2 ={ab|a ∈∑1, b ∈ ∑2}
例: {0, 1} {a, b} ={0a, 0b, 1a, 1b}
字母表∑的n次幂( power):长度为n的符号串构成的集合
∑0 ={ ε }
∑n =∑n-1 ∑ , n ≥0例: {0, 1}3 ={0, 1} {0, 1} {0, 1}={000, 001, 010, 011, 100, 101, 110, 111}
字母表的正闭包(positive closure):长度正数的符号串构成的集合:
∑+ = ∑ ∪∑2 ∪∑3 ∪…
例:{a, b, c, d }+ = {a, b, c, d,aa, ab, ac, ad, ba, bb, bc, bd, …, aaa, aab, aac, aad, aba, abb, abc, …}
字母表的克林闭包(Kleene closure):任意符号串(长度可以为零)构成的集合:
∑* = ∑0 ∪∑+ = ∑0 ∪∑ ∪∑2 ∪∑3 ∪…
例:{a, b, c, d }* = {ε, a, b, c, d,aa, ab, ac, ad, ba, bb, bc, bd, …, aaa, aab, aac, aad, aba, abb, abc, …}
例 3.1 令∑={a,b},则∑上正规式的例子如下,
a、a︱b、ab、(a︱b)* 、(a︱b)*a,
且 L(a)={a}
L(a︱b)=L(a)∪L(b)= {a}∪{b} = {a,b}
L((a︱b)*)=L(L(a︱b))*=({a,b})*={a,b}*
L((a︱b)*a)=L((a︱b)*)·L(a)= {a,b}*{a}【集合运算更有利于计算机的操作】
两个正规式e1和e2相等,是指正规式e1和e2计算值相等(即L(e1)= L(e2)),记为e1= e2 。
设r,s,t为正规式,则正规式有如下定律:
1. 交换律:r︱s = s︱r
2. 结合律:(r︱s)︱t = r︱(s︱t)
(r·s)·t = r·(s·t)
3. 分配律:r·(s︱t)= r·s︱r·t
(s︱t)·r = s·r︱t·r
(1) 描述“标识符”单词的正规式
a(a︱b)*
其中,∑={a,b},a —— 字母, b —— 数字
正规集 : L(a(a︱b)*)={a}{a,b}*
(2) 描述“整数”单词的正规式
dd*︱+dd*︱-dd
其中,∑={+,-,d}, d —— 数字
正规集: L(dd*︱+dd*︱-dd*)={+,-, ε}{d}{d}*
正规式和正规文法之间的转换
如果正规式r和文法G,有L(r)=L(G)则称正规式r和文法G是等价的。
转换方法:
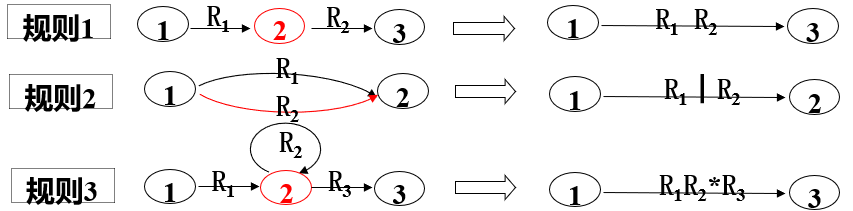
设∑上正规式r,则等价文法G=(VN,VT,P,S)。其中,VT=∑;从形如产生式 S→r 开始,按下表规则进行转换, 直到全部形如产生式, 符合正规文法之规则形式为止,可得到P和VN 。
| 规则1 | A→xy | A→xB,B→y |
|---|---|---|
| 规则2 | A→x*****y | A→xB,A→y;B→xB,B→y |
| 规则3 | A→x︱y | A→x, A→ y |
| 注:A,B∈V |
逆过程
| 规则1 | A→xB,B→y | A→xy |
|---|---|---|
| 规则2 | A→xA︱y | A→x*y |
| 规则3 | A→x, A→ y | A→x |y |
有穷自动机
对应的是识别观点。
有穷自动机首先包含一个有限状态的集合,还包含了从一个状态到另外一个状态的转换。有穷自动机看上去就像是一个有向图,其中状态是图的节点,而状态转换则是图的边。此外这些状态中还必须有一个初始状态和至少一个接受状态。
这里提到的自动机特指有限状态自动机,简称为FA,根据状态转移的性质又分为确定的自动机(DFA)和非确定的自动机(NFA)。FA的表达能力等价于正规表达式或者正规文法。FA可以看做是一个有向带权图,图的顶点集合称为自动机的状态集合,图的权值集合为自动机的字母集合。
DFA、NFA和正则表达式是等价的。
转换图 (Transition Graph)
结点:FA的状态
初始状态(开始状态):只有一个,由start箭头指向
终止状态(接收状态):可以有多个,用双圈表示
带标记的有向边:如果对于输入a,存在一个从状态p到状态q的转换,就在p、q之间画一条有向边,并标记上a
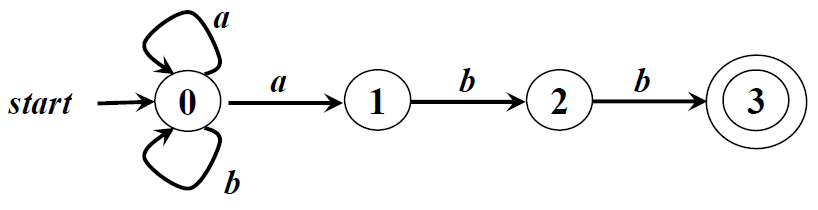
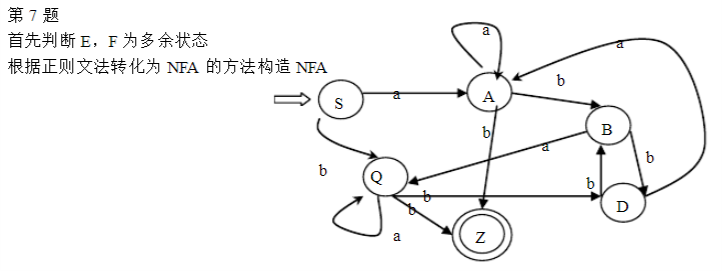
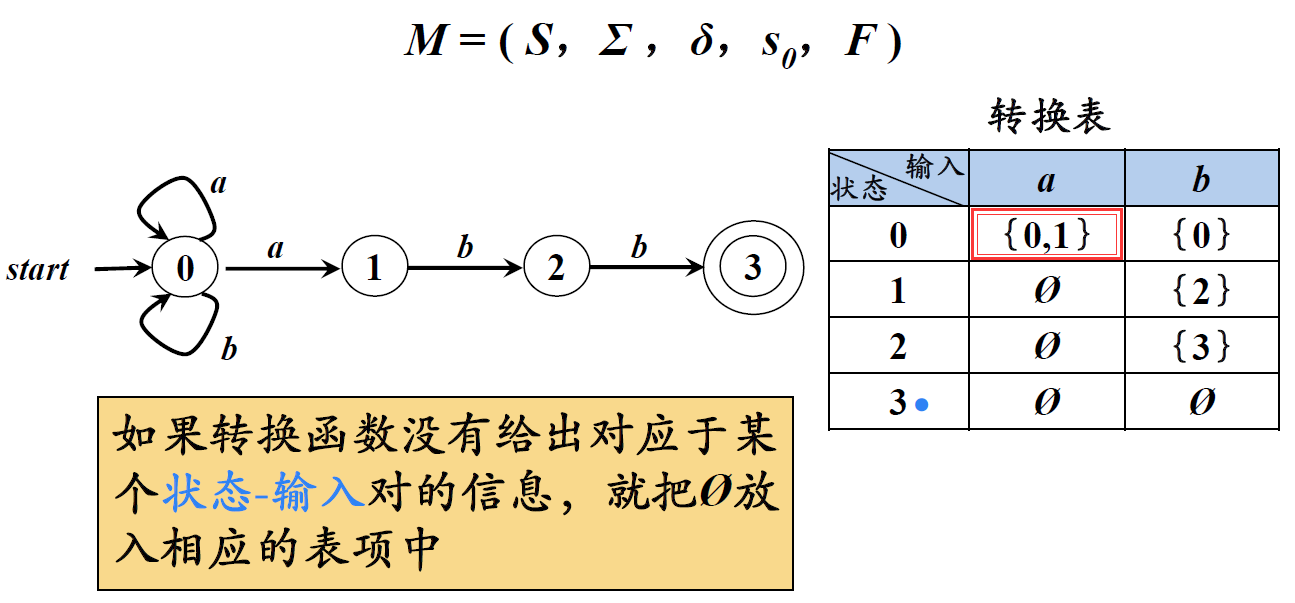
确定有穷自动机DFA
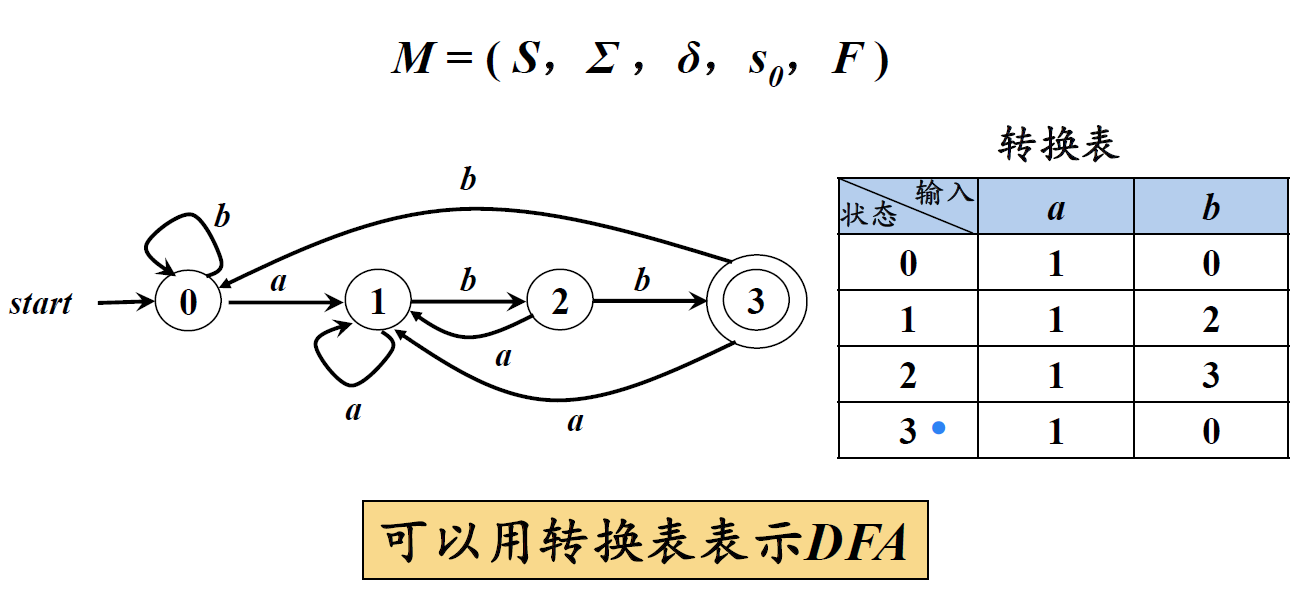
一个确定的有穷自动机DFA M是一个五元组:M=(K,Σ,f,S,Z)。
其中:
- K是非空有穷集,每个元素称为状态;
- Σ是有穷字母表;
- f是K×S→K映射,称为状态转换函数;s∈S, a∈Σ, δ(s,a)表示从状态s出发,沿着标记为a的边所能到达的状态。
- S∈K,称为开始状态;
- Z ⊂K,称为结束状态集,或接受状态集。
转换函数f可以扩充为f’: K×Σ*→K映射,并以f替代f’使用。
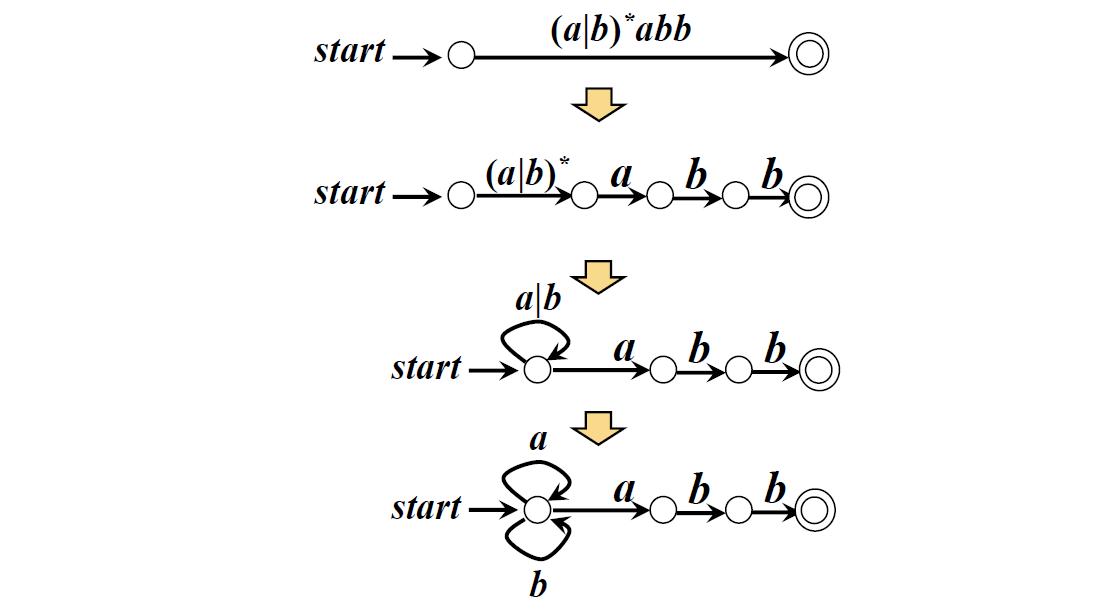
上图中r=(a|b)*abb;状态1:串以a结尾;状态2:串以ab结尾;状态3:串以abb结尾;
DFA识别的语言
设DFA M=(K,Σ,f,S,Z),如果α∈Σ*,f’(S,α)∈Z,则称符号串α是DFA M所接受(或识别)的。DFA M所接受的符号串的集合记为L(M),即:
L(M)={α︱α∈Σ*,f’(S,α)∈Z}。
一个DFA M=(K,Σ,f,S,Z),以带权有向图G=(V,E)观点,还可采用图形直观描述:
- 顶点表示状态(即V=K)
- 加上粗箭头的顶点表示开始状态
- 双圈顶点表示接受状态
- 权为a的弧<A,B>(∈E)表示f(A,a)=B。
f(A,a)=B也读作“状态A经过a转换到状态B”。
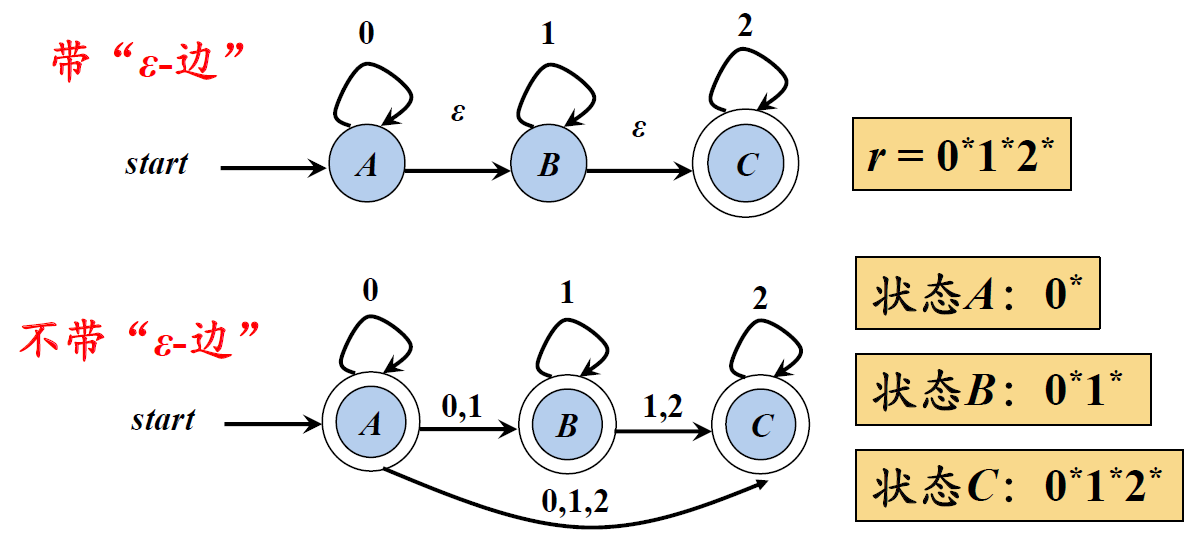
不确定有穷自动机NFA
一个不确定的有穷自动机NFA M是一个五元组:M=(K,Σ,f,S,Z)。
其中:
- K是非空有穷集,每个元素称为状态;
- Σ是有穷字母表;
- f是K×Σ∪{ε}→ρ(K)映射;f称为状态转换函数,ρ(K) 表示K之幂集。
- S ⊂K,称为开始状态集;
- Z ⊂K,称为结束状态集,或接受状态集。
上图中r=(a|b)*abb;状态1:串以a结尾;状态2:串以ab结尾;状态3:串以abb结尾;
带有“ε-边”的NFA
NFA识别的语言
设NFA M=(K,Σ,f,S,Z),如果α∈Σ*,f’(S,α)∩Z≠Φ,则称符号串α是NFA M所接受(或识别)的。NFA M所接受的符号串的集合亦记为L(M),即:
L(M)={α︱α∈Σ*,f’(S,α)∩Z≠Φ}。
自动机的等价性
如果FA M1和FA M2接受相同的符号串的集合(即L(M1)=L(M2)),则称FA M1和FA M2是等价的。
对任何非确定的有穷自动机N ,存在定义同一语言的确定的有穷自动机D
对任何确定的有穷自动机D ,存在定义同一语言的非确定的有穷自动机N
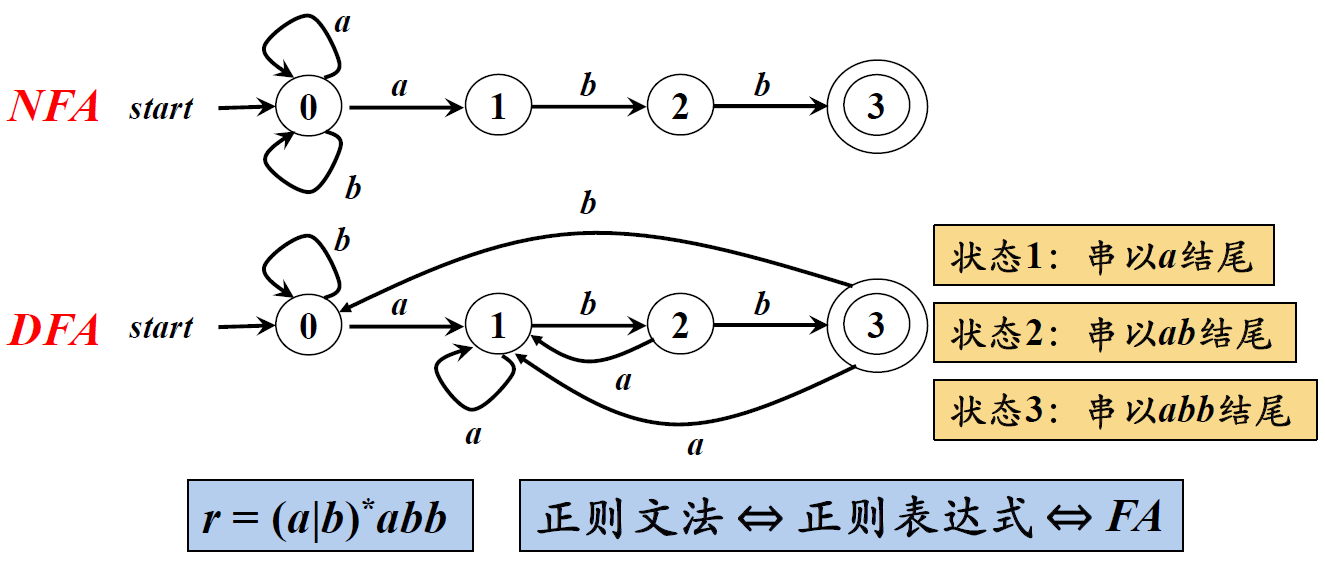
DFA和NFA的比较
两类引擎要顺利工作,都必须有一个正则式和一个文本串,一个捏在手里,一个吃下去。DFA捏着文本串去比较正则式,看到一个子正则式,就把可能的匹配串全标注出来,然后再看正则式的下一个部分,根据新的匹配结果更新标注。而NFA是捏着正则式去比文本,吃掉一个字符,就把它跟正则式比较,匹配就记下来:“某年某月某日在某处匹配上了!”,然后接着往下干。一旦不匹配,就把刚吃的这个字符吐出来,一个个的吐,直到回到上一次匹配的地方。
DFA与NFA机制上的不同带来5个影响:
- DFA对于文本串里的每一个字符只需扫描一次,比较快,但特性较少;NFA要翻来覆去吃字符、吐字符,速度慢,但是特性丰富,所以反而应用广泛,当今主要的正则表达式引擎,如Perl、Ruby、Python的re模块、Java和.NET的regex库,都是NFA的。
- 只有NFA才支持lazy和backreference等特性;
- NFA急于邀功请赏,所以最左子正则式优先匹配成功,因此偶尔会错过最佳匹配结果;DFA则是“最长的左子正则式优先匹配成功”。
- NFA缺省采用greedy量词;
- NFA可能会陷入递归调用的陷阱而表现得性能极差。
e.g.
例如用正则式/perl|perlman/来匹配文本 ‘perlman book’。如果是NFA,则以正则式为导向,手里捏着正则式,眼睛看着文本,一个字符一个字符的吃,吃完 ‘perl’ 以后,跟第一个子正则式/perl/已经匹配上了,于是记录在案,往下再看,吃进一个 ‘m’,这下糟了,跟子式/perl/不匹配了,于是把m吐出来,向上汇报说成功匹配 ‘perl’,不再关心其他,也不尝试后面那个子正则式/perlman/,自然也就看不到那个更好的答案了。
如果是DFA,它是以文本为导向,手里捏着文本,眼睛看着正则式,一口一口的吃。吃到/p/,就在手里的 ‘p’ 上打一个钩,记上一笔,说这个字符已经匹配上了,然后往下吃。当看到 /perl/ 之后,DFA不会停,会尝试再吃一口。这时候,第一个子正则式已经山穷水尽了,没得吃了,于是就甩掉它,去吃第二个子正则式的/m/。这一吃好了,因为又匹配上了,于是接着往下吃。直到把正则式吃完,心满意足往上报告说成功匹配了 ‘perlman’。
ε闭包运算
当处于某个指定状态时,如果该状态有ε边,那么,不需要吸收任何字符,就可以从该状态转换到ε边所指向的状态。
e.g:
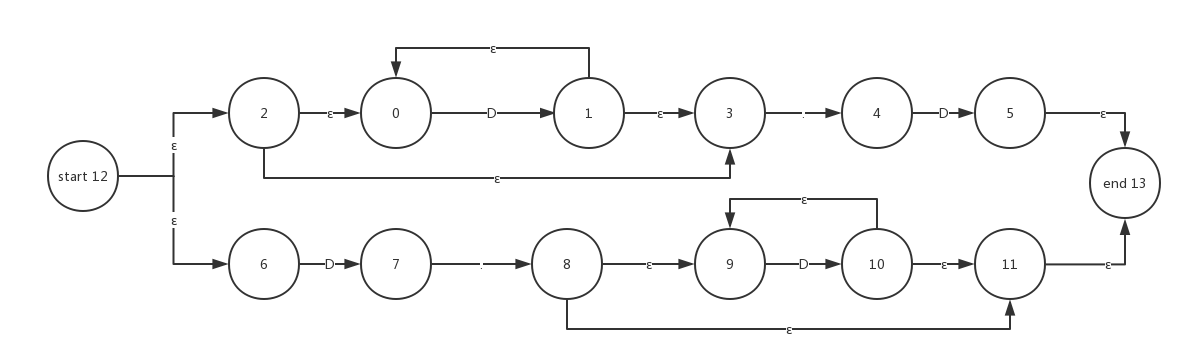
一开始,状态机处于起始状态12,
在状态12,通过ε边可直达状态2,6,
在状态2,可以通过ε边,直达状态0,3。也就是说,当处于状态12时,通过ε边的连接,可以同时抵达状态的集合是 {12,2,6,0,3}。
通过一个状态,推算出它能同时抵达的状态集合,这个状态集合称作ε闭包集合,这种运算称之为ε闭包运算:
ε-closure(12) = {12, 2, 6, 0, 3}。
接下来读入字符1,我们从闭包集合中看看,哪个状态节点有能够吸收数字的转换边。从上图观察,我们发现,
状态6和0,拥有吸收数字字符的转换边。
状态6吸收一个数字字符后,跳转到状态7,
状态0吸收字符1后,跳转到状态1,
这样我们可以说,状态集合{12, 2, 6, 0, 3} 在吸收字符1后,跳转到集合{1,7},
后面这个集合{1,7},我们称为转移集合(move set), 我们把这种跳转运算标记如下:
move({12, 2, 6, 0, 3}, D} = {1, 7}。
NFA到DFA转换方法(子集法)
设 NFA M=(K,Σ,f,S,Z)则与之等价的DFA M¢=(K’,Σ’,f’,S’,Z’),其中
⑴ K’=ρ(K)(ρ(K)是K全部子集之集合称为K之幂集)
⑵ Σ’=Σ
⑶ f’(q,a)=ε_closure(M(q,a))【转换闭包ε-closure(s)表示由状态s经由条件ε可以到达的所有状态的集合】
⑷ S’=ε_closure(S)
⑸ Z’={q︱q∈K’, q∩Z≠Φ}
注解:
①从FA开始状态不存在路径到达的状态,称为不可达状态。
②考虑舍弃不可达状态的转换状态之计算,子集法可以简化从S’=ε_closure(S)开始计算。
这些步骤的目的是为了消掉ε。
设 NFA M=(K,Σ,f,S,Z),子集法得到与其等价的DFA M¢=(K’,Σ,f’,S’,Z’之具体计算步骤可以是:
① 置K’为空集;
② 计算M’的开始状态S’=ε_closure(S), S’作为K’新增状态;
③ 对于K’每一新增状态q,计算出每个a∈S的转换状态p,即f’(q,a) =p=ε_closure(M(q,a))。如果p∉K’,则p作为K’新增状态;
④ 重复③,直到K’不再出现新增状态为止;
⑤ 计算接受状态集Z’={q︱q∈K’,q∩Z≠Φ}。

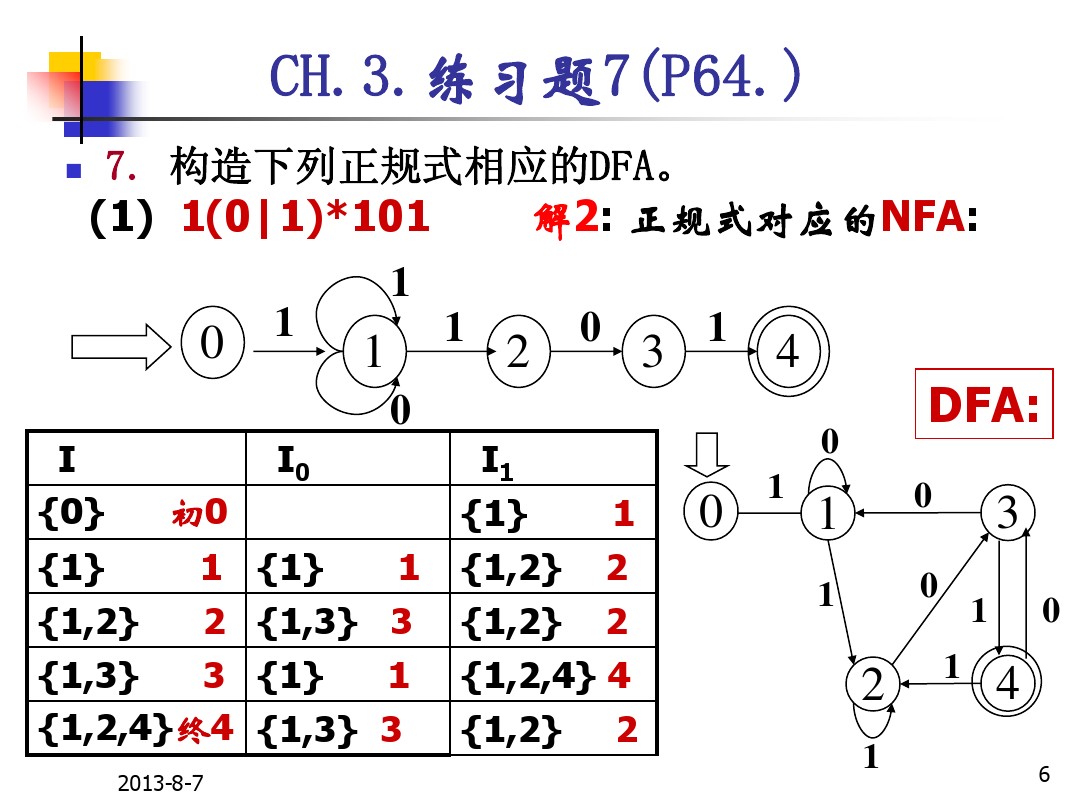
例子:
DFA的最小化
消除多余状态
- 什么是多余状态
- 从这个状态出发没有通路到达终态(也称为死状态)
- 从开始状态出发,任何输入串也不能到达的那个状态
- 如何消除多余状态
- 删除
例如:
如下为正规文法G[S]
S→aA|bQ; A→aA|bB|b;B→bD|aQ;Q→aQ|bD|b;D→bB|aA;E→aB|bF;F→bD|aE|b
构造相应的DFA。
此处我们观察到E不出现在任何产生式的右部,所以E是无效符号,(其对应的状态就是多余状态)
删除E所在的产生式之后,符号F也不出现在任何产生式的右部,则F是无效符号,
删除F及其所在产生式。此时除了文法开始符号S之外,其余非终结符都是从S可达的。
等价状态
- 何为等价状态,对于两个状态s和t
- 一致性条件:状态s和t必须同时为终态或非终态
- 蔓延性条件:对于所有输入符号,状态s和状态t必须转化到等价的状态里
DFA的化简算法:分割法
对于DFA M=(S,Σ,f,S0,Z)
首先将DFA的状态集进行初始化,分成Π=(Z,S-Z);
用下面的过程对Π构造新的划分Π new
for (Π中每个组G) do //每个组都是一个状态集
begin
把G划分成小组,G中的任意两个状态Si和Sj在同一组中,当且仅当对于Σ中任意输入符号a ,Si和Sj的a转换是到同一组中,move(Si,a) ∈Gi ,move(Sj,a) ∈Gi。这样,只要Si和Sj的a转换是到不同的组中,则说明Si和Sj是可区别的,可进行划分。在Π new中用刚完成的对G的划分代替原来的G。
end ; Π := Π new;重复执行(2),直到Π中每个状态集不能再划分(Π new= Π)为止;
合并等价状态 ,在每个G中,取任意状态作为代表,删去其它状态;
删去无关状态,从其它状态到无关状态的转换都成为无定义。
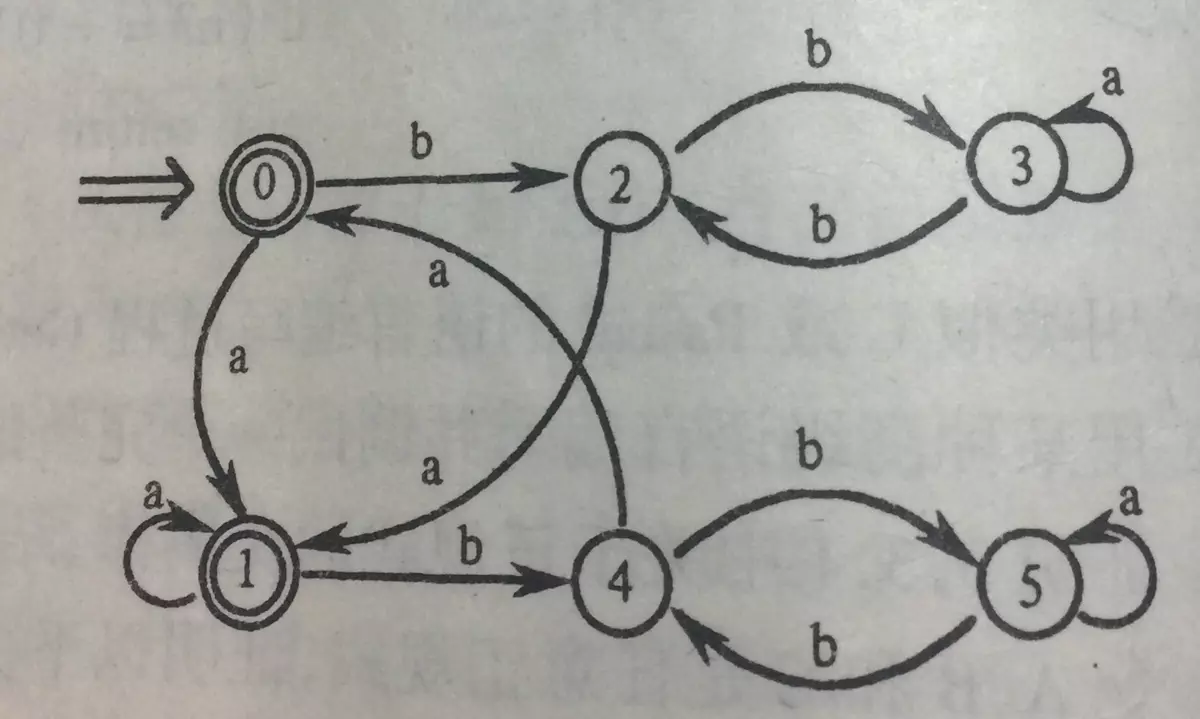
①首次划分: Π0=({2,3,4,5},{0,1})
②在G={2,3,4,5}中:f(2,a)=1,f(4,a)=0(转向终态集{0,1});f(3,a)=3,f(5,a)=5(转向非终态集{2,3,4,5}),故{2,4}和{3,5}是可区别的,得Π1=({2,4},{3,5},{0,1});
③在G={2,4}中,f(2,a)=1,f(4,a)=0(转向终态子集),而f(2,b)=3,f(4,b)=5(转向非终态子集{3,5}),所以不可区别,不再进行划分;
④考察G={3,5},f(3,a)=3,f(5,a)=5(转向非终态子集{3,5}),f(3,b)=2,f(5,b)=4(转向非终态子集{2,4}), 所以不可区别,不再进行划分;
⑤考察G={0,1},f(0,a)=f(1,a)=1(转向终态集{0,1}); f(0,b)=2,f(1,b)=4(转向非终态子集{2,4}),所以不可区别,不再进行划分;
⑦进一步进行考察,可以发现每个子集都不能再划分了;
⑧消去等价状态:{0,1}用0表示,{2,4}用2表示,{3,5}用3表示,如右图所示
⑨去掉无关状态,因DFA M’中没有无关状态,所以下图即为最后结果。
正规式和有穷自动机的等价性
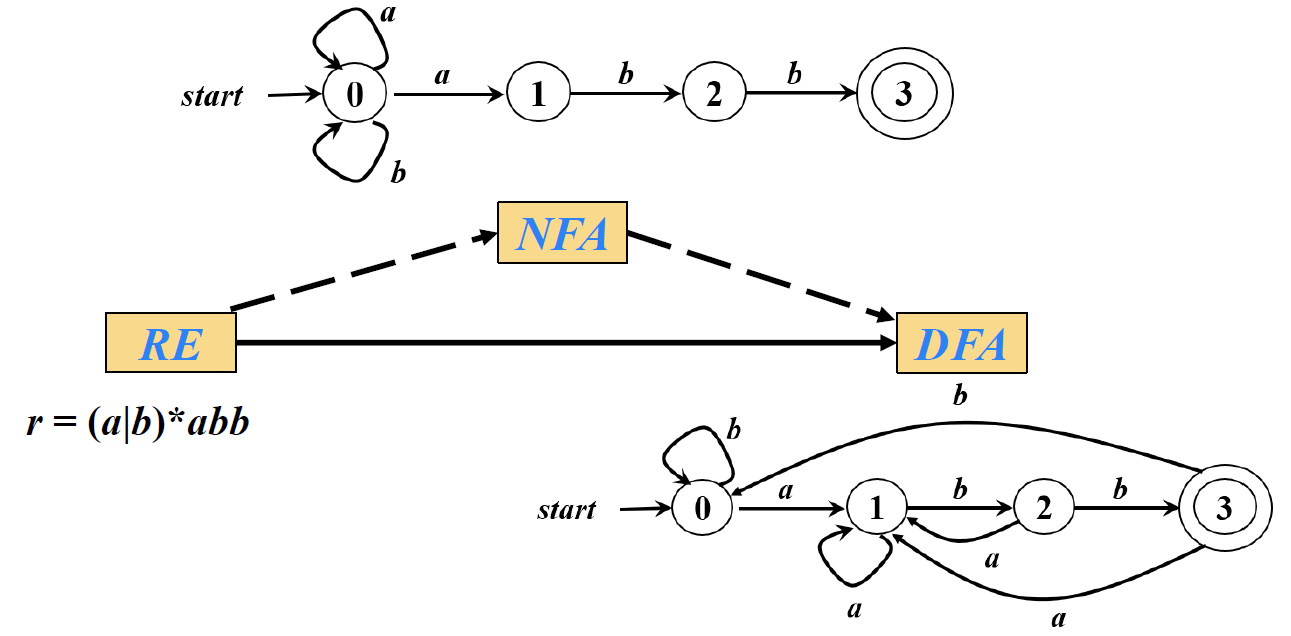
正则式 到NFA的转换
□ ε对应的NFA
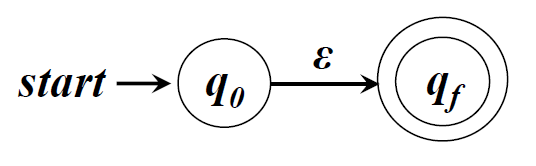
□ 字母表Σ中符号a对应的NFA

□ r = r1r2对应的NFA
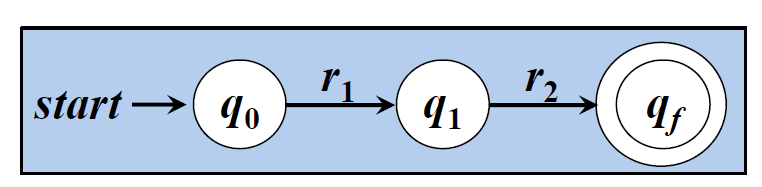
□ r = r1|r2对应的NFA
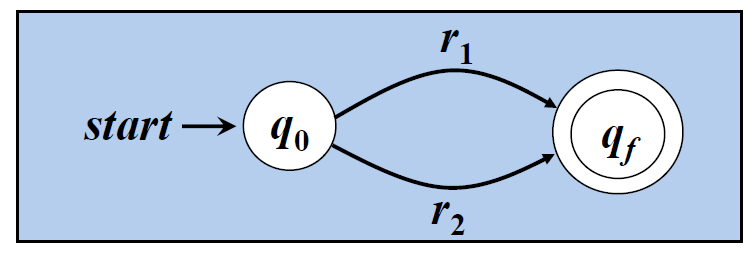
□ r = (r1)*对应的NFA
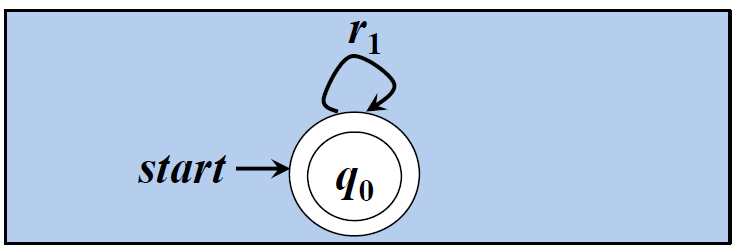
例:r=(a|b)*abb 对应的NFA
NFA到正规式的转换方法
设NFA M=( K,Σ,f,S,Z),则与之等价的Σ上正规式R,可以由下列方法构造。
⑴ 在NFA M上,新增两个状态X和Y作为开始状态和接受状态,且将X经ε指向M的开始状态(任意q∈K,增加f(X,ε)=q), 将将M的开始状态经ε指向Y(任意q∈Z,增加f(q, ε)=Y)。这样,得到一个与NFA M等价的、只有唯一开始状态X和唯一接受状态Y的NFA M’;
⑵ 按下列转换规则,逐步消除NFA M’中的状态,直到只剩下X和Y两个状态为止。弧上符号串,即为等价的S上正规式R。
DFA到右线性正规文法转换
要把一个 DFA 转化为正则表达式,我们可以通过将它分解为更简单的子问题来迭代求解:
- 将状态按 1、2、…、n 的顺序依次标号
- 先求任意状态 i 到 j(i 可以等于 j,即自身到自身),不经过其它状态的路径对应的正则表达式
- 求状态 i 到 j,最高只经过状态 1 的路径对应的正则表达式
- 求状态 i 到 j,最高只经过状态 2 的路径对应的正则表达式
- 依此类推……
- 求状态 i 到 j,最高只经过状态 n 的路径对应的正则表达式,即经过所有状态的路径对应的正则表达式
正规文法和有穷自动机间的转换
正规文法到NFA转换方法
设右线性正规文法G=(VN,VT,P,S),则与之等价的NFA M=(VN∪{Z},VT,f,{S},{Z}),其中VN∩{Z}=Φ,转换函数f可以由下列方法构造:
(1)如果A→a∈P , 则f(A,a)=Z;
(2) 如果A→ ε ∈P ,则f(A, ε)=Z;
(3)如果A→aB∈P, 则f(A, a)=B。
DFA到正规文法转换方法
设DFA M=(K,Σ,f,S,Z),则与之等价的右线性正规文法G=(K,Σ,P,S),其中规则集转换P可以由下列方法构造:
(1) 如果 f(B,a)=C, 则B→aC∈P。
(2) 对接收状态 ∈Z, 增加S→ε
构造词法分析程序的技术线路
(1)依据给定的源语言之单词集,设计其正规文法或正规式;
(2)之后等价地转换成非确定有穷自动机;
(3)再通过子集法将其确定化,最终将确定有穷自动机最小化;
(4最后依据最小化确定有穷自动机,设计词法分析程序。
自顶向下语法分析方法
分析思想
自顶向下语法分析方法(即推导法)是从文法开始符S出发,逐步进行推导,以证实S=>α的推导过程是否存在的方法。
问题是每步推导会面临两次多种可能选择:
⑴ 选择句型中哪一个非终结符进行推导
⑵ 选择非终结符的哪一个规则进行推导
问题⑴可以采用最左推导解决。问题⑵通常需要穷举每一个规则的可能推导,即不确定的自顶向下语法分析。具体思想是:
一旦寻找到一个符号串α之推导过程,便结束穷举过程,断定符号串α是句子。
只有当穷举全部可能的推导,而没有一个符号串α之推导过程的时候,才可以断定符号串α不是句子。
递归向下分析
递归向下的语法分析可能需要回溯(aka需要重复扫描输入),考虑以下文法: S -> aBc ,B -> bc | b ,当我们用递归向下分析,输入为abc时,语法树如下图:
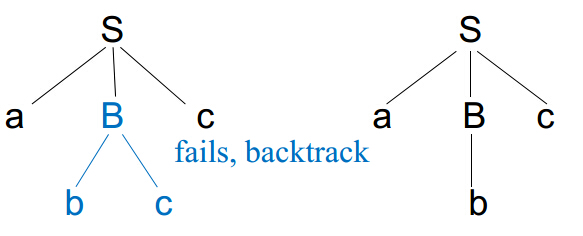
当我们第一次匹配时识别失败了(a匹配a,bc匹配B,最后一个c未匹配到),输入必须回到b,用B的另外一种方式匹配。
递归向下的分析十分直观,实现起来也比较方便,但效率较低,所以一般不采用。递归向下的分析方法实际上是深度优先搜索+回溯。而下面要说的预测分析则是用高效的动态规划来实现语法分析。
递归预测向下分析
在讨论使用动态规划的预测向下分析之前,我们先来看一种特殊的预测向下分析。它在本质上也是递归的,唯一的区别在于它不需要回溯。考虑以下文法:A -> aBb | bAB,伪代码实现如下:
proc A {
case 当前标记 {
‘a’:匹配a, 移动到下个标记;
调用函数B;
匹配b, 移动到下个标记;
‘b’:匹配b,移动到下个标记;
调用函数A;
调用函数B;
}
}
其实这种分析方式与前者的区别就在于它用了case语句来预测A的两种可能性,从而做出不同的判断。但这种方式的效率也是不如动态规划的。
非递归预测向下分析
非递归预测向下分析是表驱动的分析方法,也叫做LL(1)分析。第一个”L”表示从左到右扫描。第二个”L”表示产生最左推导。”1”表示每次只要往前走一步就可以决定语法分析的动作。
所谓表驱动就是通过查表的方式来分析一个输入流是否符合文法。假设我们已经得到了这张语法分析表,现在来具体分析这种方式是如何工作的。
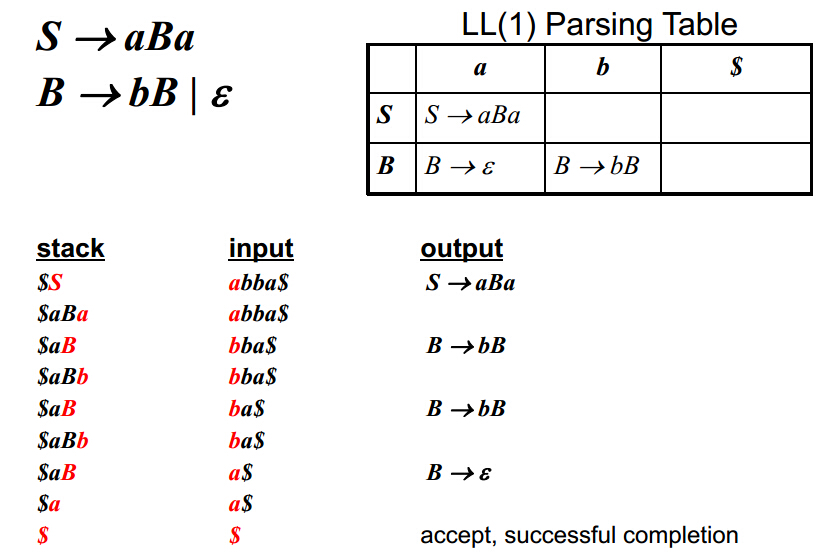
首先我们需要一个栈来存储start symbol,即语法树的根。然后从表中查找当栈顶为S,输入为a时对应的文法,然后将S替换为aBa(注意入栈顺序),然后a与输入的a匹配,非终结标志B对应到了b,此时查找表中相应的文法,将B弹出栈,将bB压入栈(注意顺序)。以此类推直到栈底的终止字符匹配到了输入的终止字符,表示匹配成功。
上面是实例,下面我们给出一个高度的分析行为概括:
当栈顶为X,当前输入为a时,有以下四种分析行为:
1.如果X和a都为终止符号$,匹配成功,停止匹配。
2.如果X和a都是同一种终结标志(terminal symbol),将X弹出栈,将输入移动到下个标志。(表示该标志成功匹配,准备匹配下个标志)
3.如果X是非终结标志(nonterminal symbol),查询语法分析表,找到[S,a],如果[S,a]为 X->Y1Y2Y3…Yk,则将Y1Y2Y3…Yk逆序放入栈中。(即Y1为栈顶)
4.不符合以上三种情况,匹配失败,进入错误恢复模式。
FIRST集的定义
设文法G=(VN,VT,P,S),则FIRST(α)={a︱α=>*a β,a∈VT,α,β∈V *}
特别地,α=>*ε,约定ε∈FIRST(α)。
FIRST(α)是由α可以推导以终结符号开头符号串的头符号集合。如果所有非终结符右部的FIRST集合两两相交为空,可以使用确定的最左推导。
计算规则如下:
1.如果X是终结符号,first(X)={X}
2.如果X是非终结符号且X->ε是一个文法规则,那么ε属于first(X)
3.如果X是非终结符号且X->Y1Y2Y3…Yn是一个文法规则,那么:①如果终结符号a在first(Yi)中且ε在所有的first(Yj) (j-1,2,…i-1)中,那么a也属于first(X) ②如果ε在所有的first(Yj) (j=1,2…n) 那么ε也属于first(X)
4.如果X本身为ε,那么first(X)={ε}
以上的规则将一直使用直到没有元素能够加入到任何first()当中。
如A->aB | CD
这里面包含了组成First(A)的两种情况:
以终结符开头,当然要把这个终结符(a)放到A的First里
以非终结符开头,先把C的First放到A的First里
FOLLOW集的定义
一般形式:
输 入 串: a1a2……ai-1 ai……an
句型推导:S=>* a1a2……ai-1 Aβ
如果使用空规则,意味着需要:β =>* ai……an
则有句型: S=>* a1a2……ai-1 A ai……an
设文法G=(VN,VT,P,S),则FOLLOW(A)={a︱S=>* αAβ,A∈VN, a∈FIRST(β),α,β∈V*}
(或者:FOLLOW(A)={a︱S =>* ···Aa···,A∈VN,a∈VT })
follow(A):从A之后可以立即得到(可以理解为与A相邻)的终结符号的集合,其中A是非终结符号。
如果对非终结符A,有一条空规则,则A的FOLLOW集合和A的非空右部的FIRST集合两两相交为空,可以使用确定的最左推导。
计算规则如下:
1.如果A->aBb是一个文法规则,那么所有在first(b)中的元素除了ε都包含在follow(B)中。
2.如果A->aB是一个文法规则或者A->aBb是一个文法规则且ε包含在first(b)中,那么在follow(A)中的所有元素都在follow(B)中。即follow(A)属于follow(B)
以上的规则也将一直使用直到没有元素能够加入到任何follow()当中。
如S->(L) | aL | LC
找Follow的三种情况:
先在候选式(右边)中找到该非终结符,如L(注意例中只有一个定义,但找Follow要看到所有右边出现该非终结符的)如果L的右边是终结符, 那么这个终结符加入L的Follow
如果L的右边是非终结符, 那么把这个非终结符的First除去空加到L的Follow中
如果L处在末尾,那么,’->’左边符号的Follow成为L的Follow
另外要注意的是:
开始符号的Follow中要加上‘#’


SELECT集的定义
$$
设文法G=(V_N,V_T,P,S),A\in V_N,A\to{\alpha}\in P,则\
SELECT(A\to{\alpha})=\begin{cases}
FIRST(\alpha),&(\alpha\not\Rightarrow\star\varepsilon)\
(FIRST(\alpha)-{(\varepsilon)})\cup(FOLLOW(A))&(\alpha\Rightarrow\star\varepsilon)\
\end{cases}
$$
SELECT(A→α)称为规则A→α的选择集。它是FIRST(α)和FOLLOW(A)组成,是终结符号集VT的子集。
LL(1)文法
文法G是LL(1)的,当且仅当G的任意两个具有相同左部的产生式A→α∣β满足下面的条件:
不存在终结符a使得α和β都能推导出以a开头的串。
α和β至多有一个能推导出ϵ
如果$\beta \Rightarrow^*{\epsilon}$⇒则$FIRST(α)∩FOLLOW(A)=Φ$
如果$α\Rightarrow^*{\epsilon}$⇒ 则$FIRST(β)∩FOLLOW(A)=Φ$
因为如果$\beta \Rightarrow^*{\epsilon}$⇒ 那么$SELECT(β)$就包含了$FOLLOW(A)$,所以$FIRST(\alpha)$就不能包含$FOLLOW(A)$中元素。不然两个的SELECT集将会相交。同一非终结符的各个产生式的可选集互不相交
判定
检查产生式中是否有含有左递归或左公因子:
含有左递归或左公因子的文法一定不是LL(1)文法;
不含有左递归或左公因子的文法也不能确定是否为LL(1)文法;计算每个产生式的FIRST集:
①如果这个产生式右部第一个字符是终结符,那么这个终结符就属于它的FIRST集。
②如果这个产生式右部第一个字符是非终结符,那么这个非终结符的FIRST集就属于它的FIRST集。
如果这个非终结符的FIRST集中含ε,那么后面的字符如果是终结符……
③如果这个产生式右部可以推出ε,那么ε也属于它的FIRST集。
计算每个非终结符的FOLLOW集:
首先向开始符号的FOLLOW集中添加
#,然后对于所有非终结符,不断的找含有它的产生式右部:①该非终结符后面的字符若是终结符,那么这个终结符就属于它的FOLLOW集;
②该非终结符后面的字符若是非终结符,那么这个非终结符的FIRST()集中的所有元素就属于它的FOLLOW集;
如果这个非终结符的FIRST()集中含ε,将ε删去,同时将这个产生式左部FOLLOW集中的所有元素添加至它的FOLLOW集中;
注意:不需要考虑后面的字符了,因为已经包含在FIRST()集中了。
计算每个产生式的SELECT集:
①如果这个产生式可以推出ε,那么它的SELECT集是
{FIRST(该产生式右部)-ε}∪FOLLOW(该产生式左部的非终结符)。②如果这个产生式不能推出ε,那么它的SELECT集是
{FIRST(该产生式右部)}。检查相同左部产生式的SELECT集的交集:
检查相同左部产生式的SELECT集的交集,如果全为空集说明该文法是LL(1)文法,反之则不是。
非LL(1)文法到LL(1)文法的等价变换
但下面讨论的等价变换方法,仅仅确保变换的等价性(即L(G)=L(G′)),不能保证变换后的文法G′一定是LL(1)文法。因此,对于变换后的文法G′,必须判别它是LL(1)文法后,方可使用确定的自顶向下语法分析方法。
提取左公共因子法
A→αβ1︱αβ2︱···︱αβn︱γ1︱γ2︱···︱γm可以推导出:
A→αB︱γ1︱γ2︱···︱γm;B→β1︱β2 ︱···︱βn
消除左递归法
有直接左递归和间接左递归和一般左递归,对于间接左递归要先化成直接;
- 直接左递归经过一次推导就可以看出文法存在左递归,如P→Pa|b。
- 间接左递归侧需多次推导才可以看出文法存在左递归,如文法:S→Qc|c,Q→Rb|b,R→Sa|a有S =>Qc =>Rbc =>Sabc
消除直接左递归法
A→Aα1︱Aα2︱···︱Aαm︱β1︱β2︱···︱βn =>
A →β1 A′︱β2 A′︱···︱βn A′;A′→α1A′︱α2A′︱···︱αmA′︱ε
有文法G(E):
E→E +T |T
T→T*F | F
F→i| (E)
消除该文法的直接左递归。
解:按转换规则,可得:
E→TE’
E’→+TE’|ε
T→FT ‘
T’→*FT’|ε
F→i| (E)
消除间接左递归法
设非终结符按某种规则排序为A1,A2,…,An。
For i﹕=1 to n do
begin
For j﹕=1 to i-1 do
begin
若Aj的所有产生式为:
Aj →δ1| δ2 | … | δn
替换形如Ai → Aj γ的产生式为:
Ai →δ1γ |δ2γ | … |δnγ
end
消除Ai中的一切直接左递归
end
以文法G6为例消除左递归:
(1)A→aB
(2)A→Bb
(3)B→Ac
(4)B→d
解:用产生式(1),(2)的右部代替产生式(3)中的非终结A得到左部为B的产生式:
(1)B→aBc
(2)B→Bbc
(3)B→d
消除左递归后得到:
B→aBcB’ |dB’
B’→bcB’ |ε
再把原来其余的产生式A→aB,A→Bb加入,最终得到等价文法为:
(1) A→aB
(2) A→Bb
(3) B→(aBc|d)B’
(4) B’→bcB’|ε
c)消除文法中一切左递归的算法
递归下降分析法
通过计算的SELECT集判断编写子程序:

递归下降分析法
ParseE’函数表示进入E’的产生式,通过switch函数分离相同左部的产生式,然后依次检查产生式右部字符,如果是终结符,则通过MatchToken函数判断符合,不符合则出错;如果是非终结符,则继续递归跳转至它所对应的Parse函数。
递归下降分析法对应的是最左推导过程
优点:程序结构和层次清晰明了,易于手工实现;
对于语义加工,这种方法十分灵活;
缺点:递归调用可能带来效率问题。
预测分析法
首先根据计算出的SELECT集绘制出预测分析表

然后新建一个分析栈,向空栈中依次压入#和文法的开始符号E,然后比较剩余输入串的首字符和分析栈顶元素,如果不同,则先将分析栈顶元素出栈,然后将对应预测分析表中的产生式右部从后向前依次入栈;如果相同,则先将分析栈顶元素出栈,并将剩余输入串的首字符删去;然后重复以上过程直到栈为#,剩余输入串也为#,则表示语法匹配成功。

LL(1)分析中的一种错误处理办法
发现错误的情况:
(1) 栈顶的终结符与当前输入符不匹配;
(2) 非终结符A于栈顶,面临的输入符为a,但分析表M的M[A,a]为空 (FIRST(A)中没有a);
应急”恢复策略:
对于错误(1) 跳过输入串中的一些符号直至遇到和栈顶的终结符相同的字符为止。
对于错误((2) 跳过输入串中的一些符号直至遇到“同步符号”为止 。
同步符号的选择
(1) 把FOLLOW(A)中的所有符号作为A的同步符号。跳过输入串中的一些符号直至遇到这些“同步符号”,把A从栈中弹出,可使分析继续。(跳过A)
(2) 把FIRST(A)中的符号加到A的同步符号集,当FIRST(A)中的符号在输入中出现时,可根据A恢复分析。 (不跳过A)
自底向上优先分析
优先分析概述
优先分析法是利用句型相邻两个符号之间的所谓“优先关系”确定句柄。
优先关系由文法规则确定,其本质含义是在句型相邻两个符号中哪个符号可以优先归约。
采用简单优先分析法或算符优先分析法构造语法分析程序时,语法分析程序的总体框架如图所示。
简单优先分析法
优先关系定义
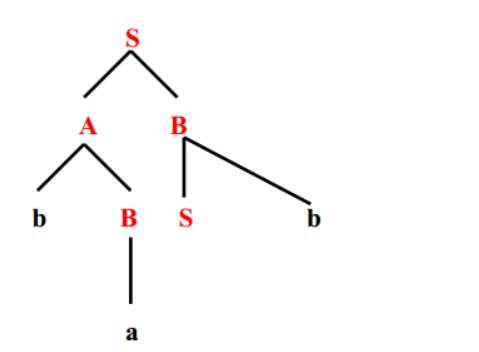
1、X和Y优先级相等,表示为 X=·Y,当且仅当G中存在产生式规则A=>···XY···。
解读:X、Y的优先级相同,当XY存在一个句柄之中,它们将同时被归约。表现在语法树中S=·b。
2、X优先级小于Y,表示为 X<·Y ,当且仅当G中存在产生式规则A=>···XB···,B=+=>Y···。
解读:X优先级小于Y,当XY存在一个句型中时,它们将不可能出现在同一个句柄中,Y一定比X先被规约。表现在语法树中b<·a。
3、X优先级大于Y,表示为 X>·Y ,当且仅当G中存在产生式规则A=>··BD···,B=+=>···X,D=*=>Y···。
解读:X优先级大于Y,当XY存在一个句型中时,它们将不可能出现在同一个句柄中,X一定比Y先被规约。表现在语法树中a>·S。
X和Y的优先级为空,表示在文法的任何句型中都不会出现该符号对相邻出现的情况。
简单优先文法定义
一个文法是简单优先文法,需要满足以下两个条件:
- 在文法符号集中V,任意两个符号之间必须之后一种优先关系存在。(显然满足)
- 在文法中,两个产生式不能有相同的右部。
简单优先分析法的操作步骤
将输入输入串a
1a2···an#依次压栈,不断比较栈顶符号ai和下一个待输入符号aj的优先级,若ai>·aj则进行下一步,否则重复此步骤。解读:停止条件是a
i>·aj表示前面输入串一定比后面先归约,所以只需要在前面找句柄就行了。栈顶符号a
i即为句柄尾,从此处向左寻找句柄头ak,满足ak-1<·ak。解读:从后向前找a
k-1<·ak表示ak之前的输入串一定比ai···ak后归约,由此确定现在就是要归约ai···ak。由句柄a
i···ak在文法中寻找右部为ai···ak的产生式;找到则将句柄替换为相应左部,找不到则说明该输入串不是该文法的句子。重复以上步骤直到归约完成。
算符优先分析法
基本概念
**算符文法(OG)**:文法G中没有形如A=>···BC···的产生式,其中B、C为非终结符,则G为算符文法(operator grammar)。
也就是说产生式的右部不能出现两个非终结符相邻,就好像算式中两个操作数相连。
算符文法的两个性质:
①算符文法中任何句型都不包含两个相邻的非终结符。②如果Ab(bA)出现在算符文法的句型y中,则y中含b的短语必含A,含A的短语不一定含b。**算符优先文法(OPG)**:一个不含ε产生式的算符文法G,任意终结符对(a,b)之间最多只有一种优先关系存在,则G为算符优先文法(operator precedence grammar)。
以算式类比,也就是说我们只关心算符之间的优先关系,不关心操作数的优先关系,·利用算符的优先性和结合性来判断哪个部分先计算(归约)。
注意 :这里的优先关系与简单优先分析法中不一样。
a、b为终结符,A、B、C为非终结符
a和b优先级相等,表示为
a=·b,当且仅当G中存在产生式规则A=>···ab···或者A=>···aBb···。解读:表示a、b在同一句柄中同时归约。
a优先级小于b,表示为
a<·b,当且仅当G中存在产生式规则A=>···aB···,且B=^+^=>b···或B=^+^=>Cb···。解读:表示b、a不在一个句柄中,b比a先归约。
a优先级大于b,表示为
a>·b,当且仅当G中存在产生式规则A=>··Bb···,且B=^+^=>···a或B=^+^=>···aC。解读:表示b、a不在一个句柄中,a比b先归约。
- FIRSTVT():FIRSTVT(B)={b|B=^+^=>b···或B=^+^=>Cb···,B∈V
N,C∈VN,b∈VT}【在算符优先中,非终结符只会和一个终结符相邻】 - LASTVT():LASTVT(B)={b|B=^+^=>···b或B=^+^=>···bC,B∈V
N,C∈VN,b∈VT} - 素短语:(a)它首先是一个短语,(b)它至少含一个终结符号,(c)除自身外,不再包含其他素短语。
最左素短语定理

FIRSTVT()的构造算法
原理:
①如果有这样的表达式:A=>a···或者A=>Ba···,那么a∈FIRSTVT(A)。
②如果有这样的表达式:B=>A···且有a∈FIRSTVT(A),则a∈FIRSTVT(B)。
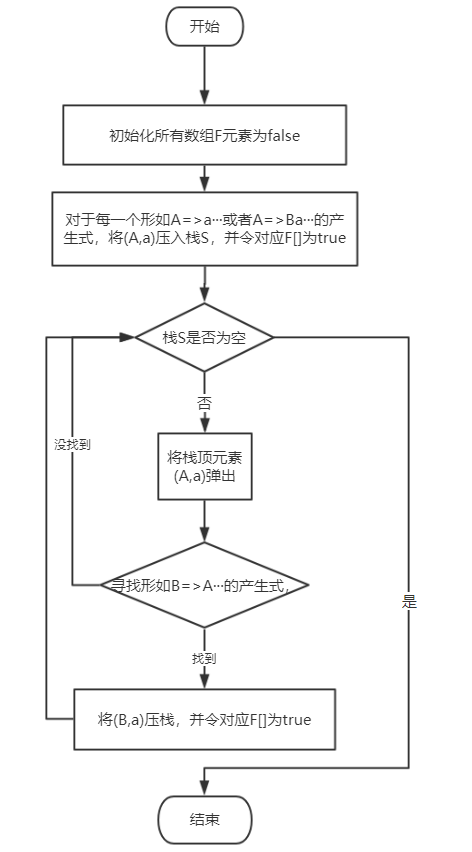
算法:
数据结构:
布尔数组F[m,n],m为非终结符数量,n为终结符数量,为真时表示对应a∈FIRSTVT(A)。
栈S:暂存用于进行原理②的元素。
流程图:
算符优先关系矩阵的构造算法
原理
=·关系
查看所有产生式的右部,寻找A=>···ab···或者A=>···aBb···的产生式,可得a=·b。
<·关系
查看所有产生式的右部,寻找A=>···aB···的产生式,对于每一b∈FIRSTVT(B),可得a<·b。
>·关系
查看所有产生式的右部,寻找A=>··Bb···的产生式,对于每一a∈LASTVT(B),可得a>·b。
算法:
1
2
3
4
5
6
7
8
9
10
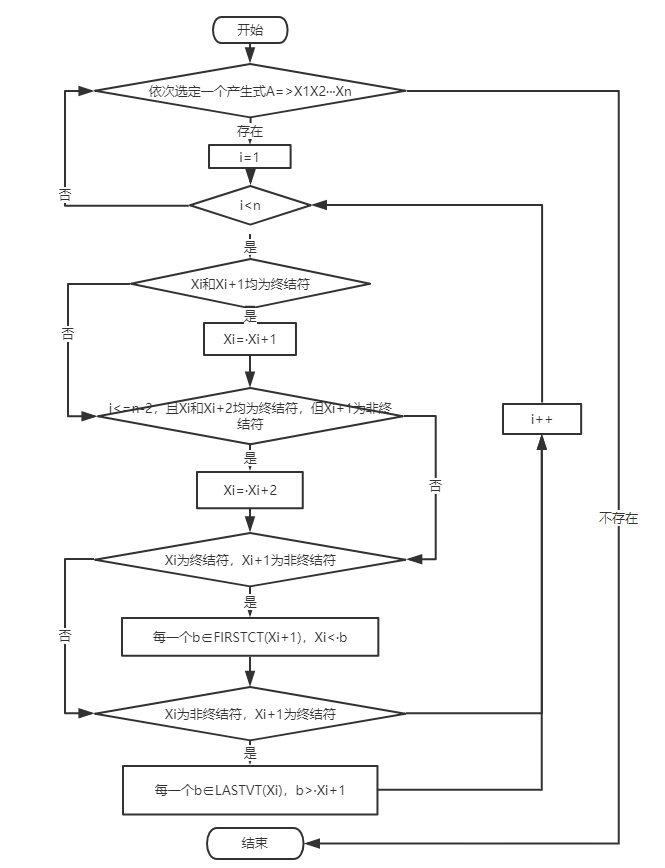
11
12for 每条规则U::= x1 x2…xn do
for i:=1 to n-1 do
begin
if xi和xi+1均为终结符, THEN 置 xi=xi+1
if i≤n-2,且xi和xi+2都为终结符号但xi+1为非终结符号 then 置 xi=xi+2
if xi为终结符号xi+1为非终结符号 then
for FIRSTVT(xi+1)中的每个b do 置xi<b
if xi为非终结符号xi+1为终结符号 then
for LASTVT(xi)中的每个a do 置a>xi+1
end流程图:
算符优先分析法
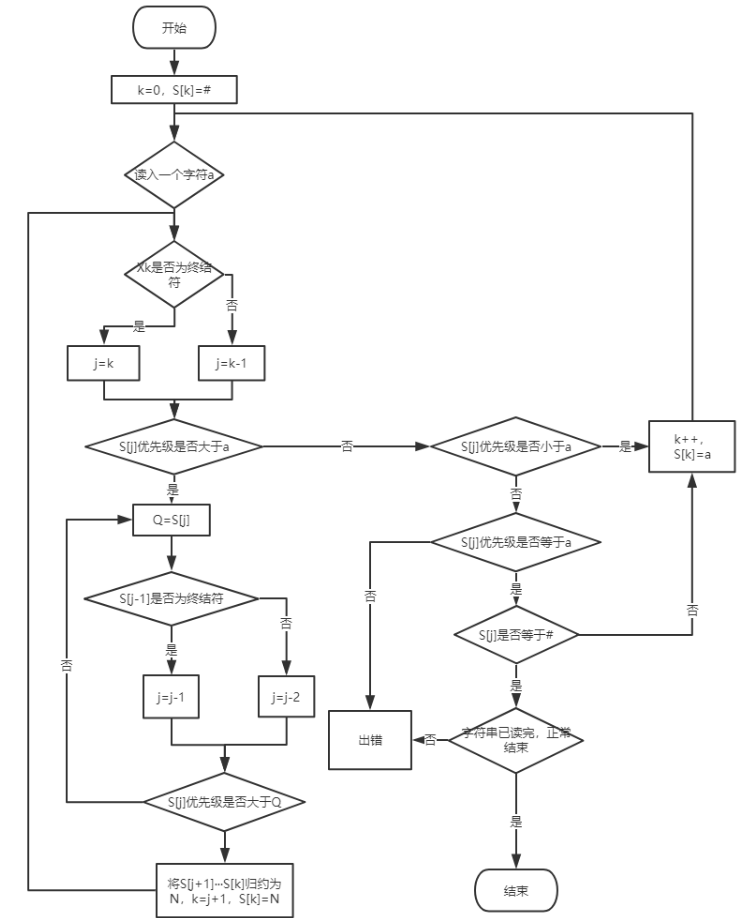
实现算符优先分析法:找句型的最左子串(最左素短语)【在语法树中,位子在句型最左边的那个素短语】并进行规约。
具体实现:当栈内终结符的优先级<或=栈外终结符的优先级时,移进;当栈内终结符的优先级>栈外终结符的优先级时,表明找到了素短语的尾,再往前找其头,并进行规约。
读入字符串为X1X2···Xn#
数组S[n+2]用于存放压入栈的字符
流程图:
算符优先函数
迭代法
若已知运算符之间的优先关系,可按如下步骤构造优先函数:
1、对每个运算符a(包括#在内)令f(a)=g(a)=1
2、如果a⋗b且f(a)<=g(b)令f(a)=g(b)+1
3、如果a⋖b且f(a)>=g(b)令g(b)= f(a)+1
4、如果a≐b而f(a) ≠g(b),令min{f(a),g(b)}=max{f(a),g(b)}
5、重复2~4,直到过程收敛。如果重复过程中有一个值大于2n,则表明不存在算符优先函数。
算符优先关系表
算符优先归约和规范规约
自下而上的语法分析,其分析过程为边输入单词符号,边归约,直至归约到文法的开始符号。(归约是指根据文法的产生式规则,把产生式的右部替换成左部符号)自下而上的分析方法的关键就是找到可归约串。
对于简单问题(不用考虑优先级等问题)的自下而上语法分析有以下方法:
1.移进归约,即用一个寄存符号的先进后出栈,把输入符号一个一个地移进到栈里,当栈顶形成某个产生式的候选式时,即把栈顶的这一部分替换成(归约为)该产生式的左部符号;
2.规范规约,首先了解规范规约的定义,假定α是文法G的一个句子,如果序列αn,αn-1,… ,α0满足:(1)αn=α(2)α0为文法的开始符号,即α0=S(3) 对任何i,0<i≤n,αi-1是αi把句柄(句型的最左直接短语即最左端的简单子树)替换成为相应产生式左部符号而得到的。我们称该序列是α的一个规范归约,规范规约即最左归约,可通过修剪最左简单子树实现;
3.用符号栈进行自下而上的语法分析,取一个栈作为符号栈,在分析开始时,’#’预先进栈,作为栈底符号,将输入串中的符号依次入栈并规约,’#’作为输入串的结束符。
在实际问题中往往能够需要考虑优先级,对于优先级问题有以下处理方法:(1)算符优先分析法,即定义算符之间的某种优先关系,借助这种优先关系找到可归约串并规约。这种优先关系往往是单向的,没有自反性。在算符优先分析法中将最左素短语作为可归纳串(算符优先分析一般不等于规范归约);(2)优先函数法,优先函数是把每个终结符α与两个自然数f(α)与g(α)相对应,使得若α1 <. α2,则f(α1) < g(α2),若α1 =. α2,则f(α1) = g(α2),若α1 >. α2,则f(α1) > g(α2),f称为入栈优先函数,g称为比较优先函数。