最小生成树
关于图的几个概念定义:
- 连通图:在无向图中,若任意两个顶点vivi与vjvj都有路径相通,则称该无向图为连通图。
- 强连通图:在有向图中,若任意两个顶点vivi与vjvj都有路径相通,则称该有向图为强连通图。
- 连通网:在连通图中,若图的边具有一定的意义,每一条边都对应着一个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通网。
- 生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
- 最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
最小生成树并不一定唯一
最小生成树的形成
MST性质
假设N = (V,{ E })是一个连通网,U 是顶点集V的一个非空子集。若(u , v )是一条具有最小权值(代价)的边,其中u∈U, v∈V - U,则必存在一棵包含边(u,v)的最小生成树。
证明:
剪枝-粘贴法
假设网N的任何一棵最小生成树都不包含(u,v)。设T是连通网上的一棵最小生成树,当将边(u,v)加入到T中时,由生成树的定义,T中必存在一条包含(u,v)的回路。另一方面,由于T是生成树,则在T上必存在另一条边(u’,v’),其中u’∈U,v’∈V - U,且u和u’之间,v和v’之间均有路径相通。删去边(u’,v’),便可消除上述回路,同时得到另一棵生成树T’。因为(u,v)的代价不高于(u’,v’),则T’的代价亦不高于T,T’是包含(u,v)的一棵最小生成树,和假设矛盾。
贪心策略设计(MST性质)
每个时刻,该方法生长最小生成树的一条边,并在整个策略的实施过程中,管理一个遵守下述循环不变式的边的集合A:在每遍循环之前,A是某棵最小生成树的一个子集。
循环不变式:在每遍循环之前,A是某棵最小生成树的一个子集。
处理策略:每一步,我们选择一条边不违反循环不变式的边(u,v)加入集合A,即A∪{(u,v)}仍是某棵最小生成树的子集。
这样的边称为“安全边”,因为在集合A中加入它不会破坏A的循环不变式。
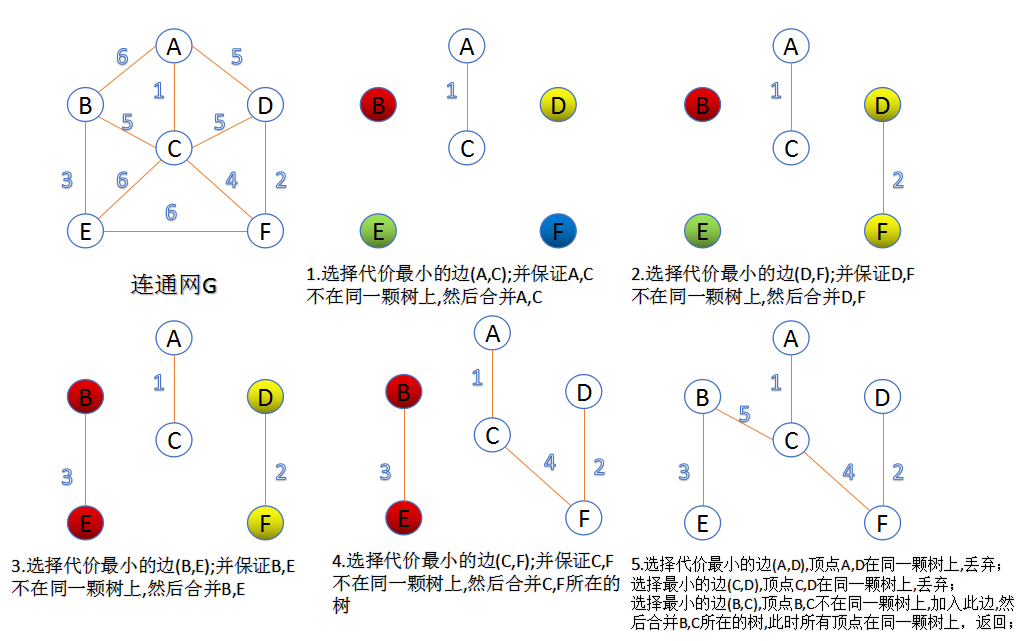
Kruskal算法(贪心算法)
初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
- 把图中的所有边按代价从小到大排序;
- 把图中的n个顶点看成独立的n棵树组成的森林;
- 按权值从小到大选择边,所选的边连接的两个顶点u
i,vi(ui,vi,应属于两颗不同的树),则成为最小生成树的一条边,并将这两颗树合并作为一颗树。 - 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
- 注意:不能生成环
Kruskal算法的时间为:O(E lgE)。
如果再注意到|E|<|V|2,则有lg|E|=O(lgV),所以Kruskal算法的时间可表示为O(E lgV)。
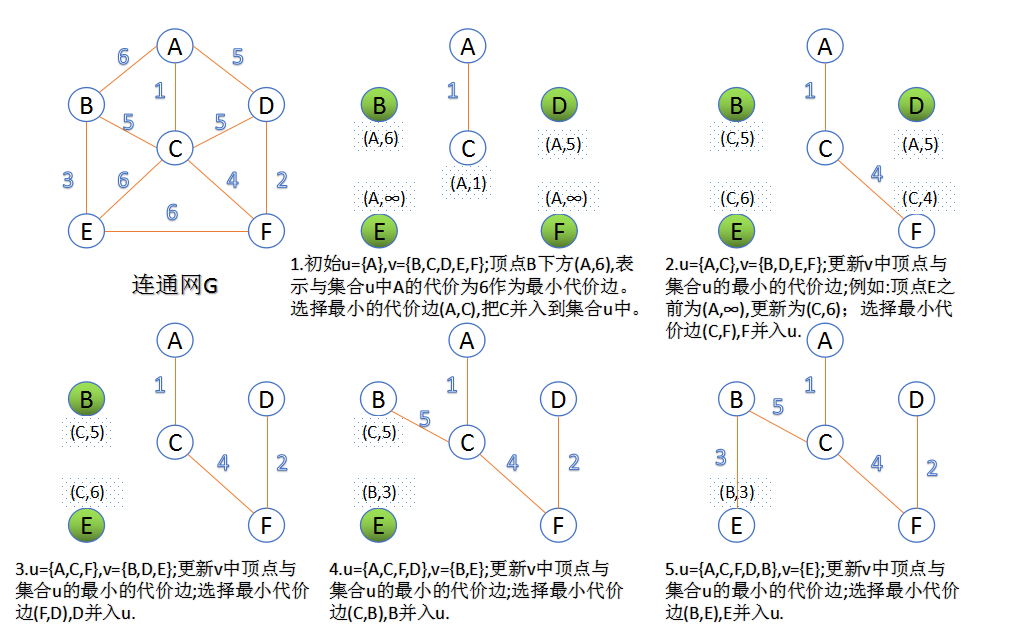
Prim算法(贪心算法)
此算法可以称为“加点法”,每次迭代选择代价最小的边(已经加到最小生成树的点可以连接的边中选择)对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
- 图的所有顶点集合为V;初始令集合u={s},v=V−u;
- 在两个集合u,v能够组成的边中,选择一条代价最小的边(u
0,v0),加入到最小生成树中,并把v0并入到集合u中。 - 重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。
- 注意不能生成环
由于不断向集合u中加点,所以最小代价边必须同步更新;需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息,
Prim算法的运行时间依赖于最小优先队列Q的具体实现。
可用二叉最小优先队列的方式实现。
每次EXTRACT-MIN的时间是O(lgV)。
EXTRACT-MIN的总时间是O(V lgV)。
其它时间:第11行的赋值操作共需O(E lgV)。
Prim算法的时间为:O(V lgV+E lgV)=O(E lgV)。
从渐进意义上看,Kruskal和Prim算法具有相同的运行时间