最大流
有一个源结点和一个汇点,从源结点向汇点“运输”货物。在不违反任何路径容量限制的条件下,从源结点到汇点运送货物的最大速率是多少——这一问题的抽象称为最大流问题
流具有三个需要注意的点!!
1、对于图中非s和t的普通结点,流进量等于流出量
2、我们非常关心总运输流量,比如这个下水道系统,究竟从s点到t点最多能运输多少立方米的水?我们把它记成|f|,这个|f|极其重要,是我们研究的目的所在。
3、当然,每条边是有运输上限的,就像某条公路车流是有上限的一样,若运输量无穷无尽,我们的研究也就没有意义了。我们将从u点到v点的运输上限,或者说是运载能力记为c(u,v)。对于从u点到v点的流量,记作f(u,v)。显然对所有边(u,v)我们有f(u,v)<=c(u,v)。
参考文章
流网络
流网络G=(V,E)是一个有向图,其中每条边(u,v)∈E均有一个非负能量c(u,v)≥0。如果(u,v)∉E,则假定c(u,v)=0。流网络中有两个特点的顶点,源点s和汇点t,假定每个顶点均处于从源点到汇点的某条路径上,就是说,对每个顶点v∈V,存在一条路径s->v->t,因此图G是连通图,且|E|≥|V|-1。
带权有向图:网络
结点:表示城市
有向边:表示运输路径和物流的方向
权重:表示运量限制
流:一条从源点到汇点的路径即路径上的流量——这种用来表示”流(flow)”的图称为“流网络”
流网络遵循以下基本性质:
(1)流量守恒:除源结点和汇点外,其它结点上物料只是“流过”,即物料进入的速率等于离开的速率;
(2)物料的生成速率和接收速率恒定且足够快、足够多,满足需要(包括源结点的输出和所有结点的输入);
(3)每条边上的容量是物料通过该边的最大速率,不能突破
流网络是一个有向图,边上定义有容量函数c:
(1) 有一个源结点s和汇点t;
(2) 有向边表示流向;
(3) 每条边上有一个非负的容量值;如果(u,v)∉E,则假定c(u,v)=0;
(4) 如果边集合E中包含(u,v)边,则图中不包含其反向边(u,v);
(5) 图中不允许有自循环;
(6) 流网络是连通图,每个结点都在从s到t的某条路径上;
(7) 除源结点外,每个结点至少有一条流入的边;
(8) 除汇点外,每个结点至少有一条流出的边;
(9) |E|>=|V|-1
标准流网络:
(1)无反向边:也称为反向平行边。一个有向图中,(v,u)、(u,v)互为反向平行边
(2)只有单一的源结点和汇点。
非标准流网络:
不满足上述要求的流网络是非标准的流网络。对于非标准的流网络可转化为标准流网络。
方法:
1)添加反向平行边
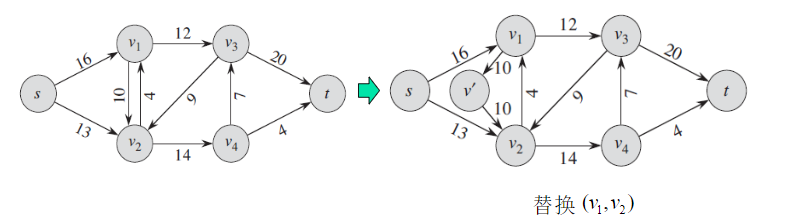
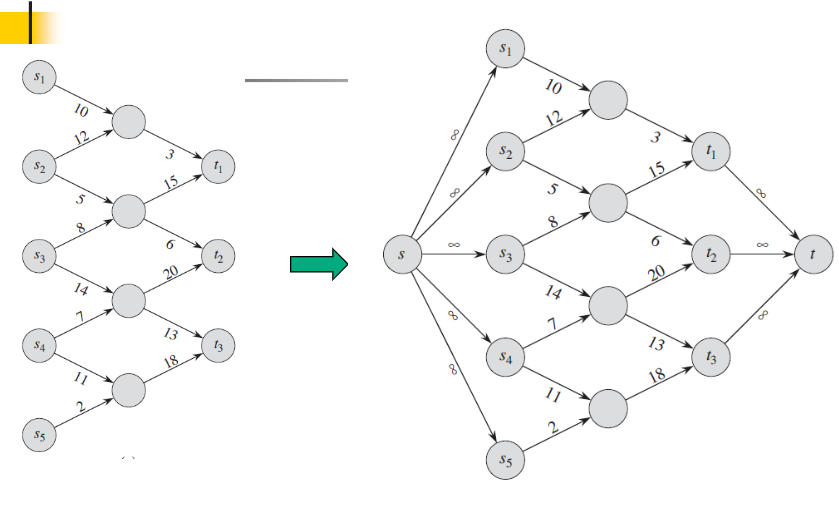
2)多个源结点和多个汇点。加入一个超级源结点s。加入一个超级汇点t。
Ford-Fulkerson方法
通过不断增加可行流值的方式找到最大流:
(1)从流值为0的初始流开始;
(2)通过某种方法,对流值进行增加;
(3)当确认无法再增加流值时,就得到最大流;
首先这个算法有个重要的工具:残存网络。残存网络其实就是具有残存容量的图。算法导论上有个普遍公式来定义残存容量: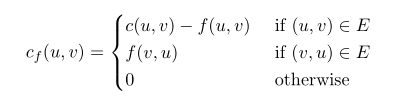
翻译一下公式,说明的就是对于两点间的残存容量定义为:
1.如果这两点连线原来就是原图的边,那么它的残存容量等于运载上限-运输流量。(就是目前你还能增加的流量的量)
2.如果这两点的反向连线是原图的边,那么它的残存容量等于那条边的运输流量。(表示目前用的运输流量,一旦该运输流量等于运载上限,运算结束)
3.其他情况是0,当做没连通。
接下来我们看看残存网络对我们的帮助:
1.残存网络中没有从s到t的路径时,最大流等于最小割容量。(没有路径就说明s到t的连线有一段已经达到了最大运载上限了,就是残存容量为0)
2.残存网络中有从s到t的路径时,最大流不等于最小割容量。