所有结点对的最短路径

问题：有一个带权有向图 G = (V, E)，V 为图的顶点集合，E 为边的集合，权重函数为 w：E → R，该函数将边映射到实数值上。我们希望找到，对于所有结点对 u，v∈V，一条从结点 u 到结点 v 的最短路径，使得结点 u 到结点 v 的路径所有边的权重之和最小。

简单来说，我们考虑的问题是如何找到一个图中所有结点之间的最短路径。

用单源最短路径算法求解：
执行|V|次单源最短路径算法，每次使用一个不同的结点作为源点，从而可以求出每个结点到其他所有结点的最短路径。

如果所有的边的权重为非负值，用Dijkstra算法：
- 用线性数组实现最小优先队列：O(V^3^+VE)=O(V^3^);
- 用二叉堆实现最小优先队列：O(VElgV)；（对稀疏图较好）
- 用斐波那契堆实现最小优先队列：O(V^2^lgV+VE)；
如果有权重为负值边，用Bellman-Ford算法：
- 一般的运行时间：O(V^2^E);
- 对稠密图，运行时间为O(V^4^)。

允许存在权重为负值的边，但不能包含权重为负值的环路

邻接矩阵

邻接矩阵是表示一个图的常用存储表示。它用两个数组分别存储数据元素（顶点）的信息和数据元素之间的关系（边或弧）的信息。
$$
W_{ij}=\begin{cases}0 &&&&&&if&i=j\有向边（i，j）的权重 &&&&&&if&i\not=j&and(i,j)\in E\NIL &&&&&&if&i\not=j&and(i,j)\notin E\\end{cases}
$$

最短路径和矩阵乘法

步骤一：分析最优解结构

一条最短路径的所有子路径都是最短路径

每条路径都是最短路径

步骤二：所有结点对最短路径的递归解

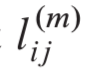
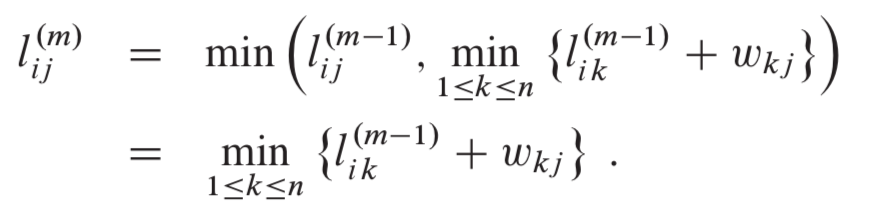
设为从i到j的一条最短路径，且这条路径最多包含m条边。我们可以得到以下的递推公式：

如果图G不包含权重为负值的环路，则对于每一对结点i和j，如果δ(i,j)<∞，则从i到j之间存在一条最短路径。并且，由于最短路径是简单路径，其中至多包含n-1条边，因此有：

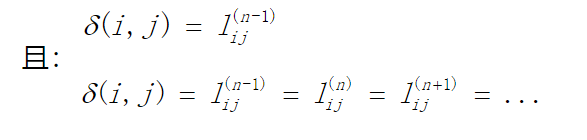
步骤三：自底向上计算最短路径权重

步骤三改进：重复平方

步骤四：构建最优解

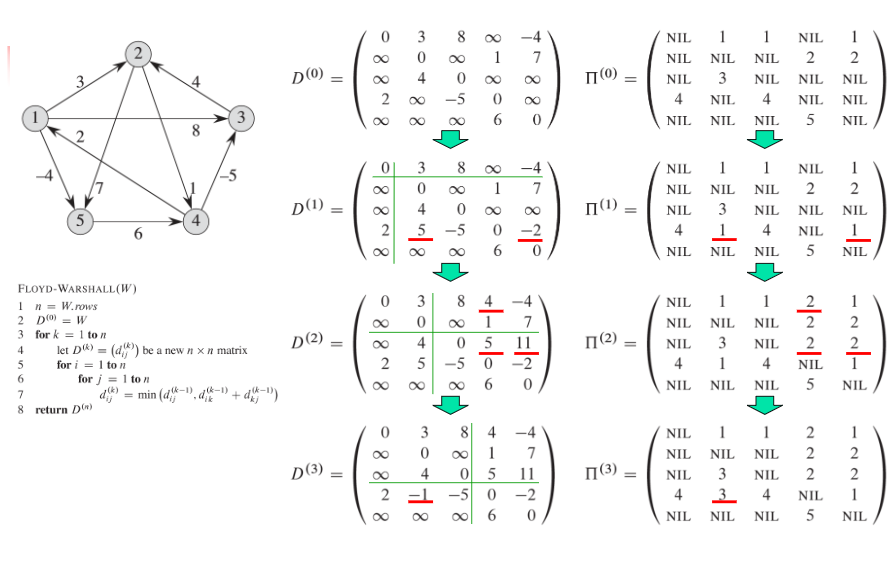
计算最短路径权重 - Floyd-Warshall 算法

采取的是动态规划策略

算法的时间复杂度Θ(V^3^)。

算法允许图中存在负权重的边，但不能存在权重为负值的环路

Floyd 算法考虑的是一条路径上的中间结点。对于任意结点对 i，j∈V，考虑从结点 i 到结点 j 的所有中间结点均取自集合 {1, 2, …, k} 的路径（该集合是 V ={1,2,3·····,n}的一个子集），并且设 p 为最短路径。

含义：

p是简单路径，且p的中间结点都不大于k。
p从i到j，仅经过集合{1,2,…,k}中的结点，但，
- 不一定经过其中的每一个结点，且与顺序无关；
- 也可能不存在这样的路径，此时p的权重等于∞

从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，算法假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，算法检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

有两种情况：

如果结点 k 不是路径 p 上的中间结点，则路径 p 上的所有中间结点都属于集合 {1, 2, …, k - 1}。
如果结点 k 是路径 p 上的中间结点，则可将路径 p 分解为两条路径，分别是结点 i 到结点 k 和结点 k 到结点 j 的路径。

简单来说，就是中间结点选自集合 {1，2，…，k - 1} 的时候的所有结点对的最短路径权重已经知道了，接下来的考虑的中间结点从集合 1，2，…，k - 1，k} 选的时候最短路径权重是多少，只需要考虑路径经过结点 k 的时候权重变化就行了，k 可将 i 到 j 的路径分为两条路径，分别是结点 i 到结点 k 和结点 k 到结点 j 的路径，而这两个的最短路径权重已经知道的（i 到 k 的最短路径的中间结点只能从集合 {1，2，…，k - 1} 选），同理 k 到 j），所以最新的权重选择经过 k 与不经过 k 时的权重较小的那个就行。

递归解

设$$d^{(k)}_{ij}$$表示从结点 i 到结点 j 的所有中间结点全部取自集合 {1，2，…，k} 的一条最短路径的权重。

k = 0 时，表示结点 i 到结点 j 的路径没有任何中间结点，因此$$d^{(0)}{ij} = w{ij} $$。

状态转移方程：
$$
d^{(k)}{ij} = \begin{cases} w{ij} & \text {if $k = 0$} \min(d^{(k-1)}{ij}, d^{(k-1)}{ik}+ d^{(k-1)}_{kj}) & \text {if $k\geq1$ }\end{cases}
$$

而因为任何路径的中间结点都属于集合{1,2,…,n}，所以k=n时，$$d^{(n)}_{ij}$$给出所有可能的从结点i到结点j的中间结点均取自集合{1,2,…,n}的一条最短路径的权重，也就是从结点i到结点j的最短路径的权重。

所以对所有的$$i,j\in V$$,有：
$$
d^{(n)}_{ij}=δ(i,j)
$$

自底向上计算最短路径权重

private void floyd(Graph G, int dist)
{
    //vexnum表示图G的顶点数
    // 计算最短路径
    for (int k = 0; k < G.vexnum; k++)
    {
        for (int i = 0; i < G.vexnum; i++)
        {
            for (int j = 0; j < G.vexnum; j++)
            {
                // 如果经过下标为k顶点路径比原两点间路径更短，则更新dist[i][j]
                int tmp = (dist[i][k] + dist[k][j]);
                if (dist[i][j] > tmp)
                {
                    dist[i][j] = tmp;
                }
            }
        }
    }
}

构建最短路径

思路：给定一个前驱矩阵 $$\prod$$，再利用递归的思想即可输出结点 i 到结点 j 的最短路径。

前驱矩阵

定义：给出的是从结点 i 到结点 j 的最短路径上结点 j 的前驱结点，i=j 或者从 i 到 j 不存在路径时为 NIL。

$$\pi^{(k)}_{ij}$$为从结点i到结点j的一条所有中间结点都取自集合{1,2, …, k}的最短路径上j的前驱结点。

怎么得到前驱矩阵？一种方法是计算权重矩阵 dist 的同时计算前驱矩阵 ∏。具体来说，与 floyd 算法思路类似，分为两种情况：
当 k = 0 时，从 i 到 j 的最短路径没有中间结点，所以，
$$
\pi^{(0)}{ij} = \begin{cases} NIL & \text {if $i = j\ or\ w{ij} = NIL$ } \i & \text {if $i \ne j\ or\ w_{ij} < NIL$ }\end{cases}
$$
当 k≥1时
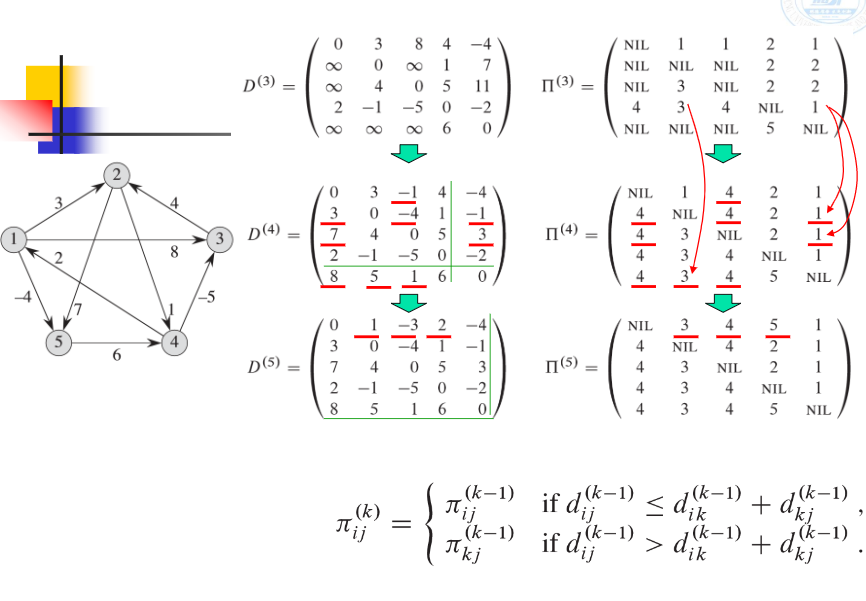
$$
\pi^{(k)}{ij} = \begin{cases}\pi^{(k-1)}{ij} & \text {if $d^{(k-1)}{ij} \leq d^{(k-1)}{ik} + d^{(k-1)}{kj}$ } \ \pi^{(k-1)}{kj} & \text {if $d^{(k-1)}{ij} > d^{(k-1)}{ik} + d^{(k-1)}_{kj}$ }\end{cases}
$$

若不经过k：

此时求从结点i到结点j的所有中间结点都取自集合{1,2,…,k}的最短路径上的j的前驱等价于求从结点i到结点j的所有中间结点都取自集合{1,2,…,k-1}的最短路径上的j的前驱。

若经过k：

此时求从结点i到结点j的所有中间结点都取自集合{1,2,…,k}的最短路径上的j的前驱等价于求从结点k到结点j的所有中间结点都取自集合{1,2,…,k-1}的最短路径上的j的前驱。

用于稀疏图的Johnson算法

在稀疏图中求每对结点之间的最短路径权重。

对稀疏图，Johnson算法优于Floyd-Warshall算法，时间复杂度可达O(V^2^lgV+VE)。

Johnson算法使用的方式相当于给每个边都加了一个权重，使得所有边都为非负数，这样就能对每个边使用较为高效的Dijkstra算法。
注意的是不能简单的给每个边加相同的值然后使得所有边都变成非负数，原因为假设从a->b有两条路径，一条权重为1+1，一条为2，本应权重和相等；如果都加1，则变成了2+2和3，不一致了，就会导致更新了不该更新的边。
Johnson比较巧妙的引入了h函数来解决这个问题，通过这个函数进行每个边的重新赋值权重

参考文章

算法描述

给定图 G = (V, E)，增加一个新的顶点 s，使 s 指向图 G 中的所有顶点都建立连接，设新的图为 G’；
对图 G’ 中顶点 s 使用 Bellman-Ford 算法计算单源最短路径，得到结果 h[] = {h[0], h[1], .. h[V-1]}；
对原图 G 中的所有边进行 “re-weight”，即对于每个边 (u, v)，其新的权值为 w(u, v) + (h[u] - h[v])；
移除新增的顶点 s，对每个顶点运行 Dijkstra 算法求得最短路径；

rhb_blog

所有结点对的最短路径

所有结点对的最短路径

邻接矩阵

最短路径和矩阵乘法

步骤一：分析最优解结构

步骤二：所有结点对最短路径的递归解

步骤三：自底向上计算最短路径权重

步骤三改进：重复平方

步骤四：构建最优解

计算最短路径权重 - Floyd-Warshall 算法

递归解

自底向上计算最短路径权重

构建最短路径

用于稀疏图的Johnson算法

算法描述

算法证明