图检索算法

图的表示

对于图G=（V，E）借助数组存储的方法有邻接矩阵表示法和邻接表表示法，边集表示法。

邻接矩阵

图的邻接矩阵（adjacent matrix）表示法是使用数组来存储图结构的方法，也被称为数组表示法。它采用两个数组来表示图：一个是用于存储所有顶点信息的一维数组，另一个是用于存储图中顶点之间关联关系的二维数组，这个关联关系数组也被称为邻接矩阵。

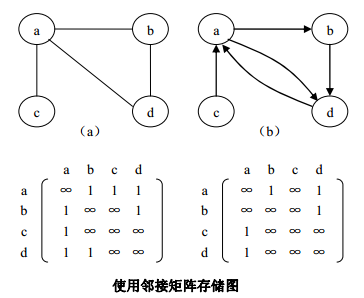
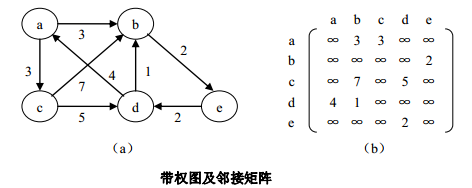
邻接矩阵有如下特性：

图中各顶点序号确定后，图的邻接矩阵是唯一确定的。
无向图和无向网的邻接矩阵是一个对称矩阵。
无向图邻接矩阵中第i行或第i列的非0元素个数即为第i个顶点的度。
有向图邻接矩阵第i行非0元素个数为第i个顶点的出度，第i列非0元素个数为第i个顶点的入度，第i个顶点的度为第i行与第i列非0元素个数之和。
无向图的边数等于邻接矩阵中非0元素个数之和的一半，有向图的弧数等于邻接矩阵中非0元素个数之和。
除完全图外，其他图的邻接矩阵有许多零元素，特别是当n值较大，而边数相对完全图的边n-1又少的多时，则此矩阵称为稀疏矩阵，非常浪费存储空间。

邻接表

邻接表（adjacency list）是图的一种链式存储方法，邻接表表示法类似于树的孩子链表表示法。

　　在邻接表中对于图G中的每个顶点vi建立一个单链表，将所有邻接于vi的顶点vj链成一个单链表，并在表头附设一个表头结点，这个单链表就称为顶点vi的邻接表。

邻接表中共有两种结点结构，分别是边表结点和表头结点。

邻接表中的每一个结点均包含有两个域：邻接点域和指针域。

邻接点域用于存放与定点vi相邻接的一个顶点的序号。
指针域用于指向下一个边表结点。

边表结点由3个域组成：

邻接点域（adjvex）指示与定点vi邻接的顶点在图中的位置。
链域（nextdge）指向下一条边所在的结点。
数据域（info）存储和边有关的信息。

头结点由2个域组成：

链域（firstedge）指向链表中的第一个结点之外。
数据域（data）存储顶点相关信息。

如下图为邻接表的存储示例：

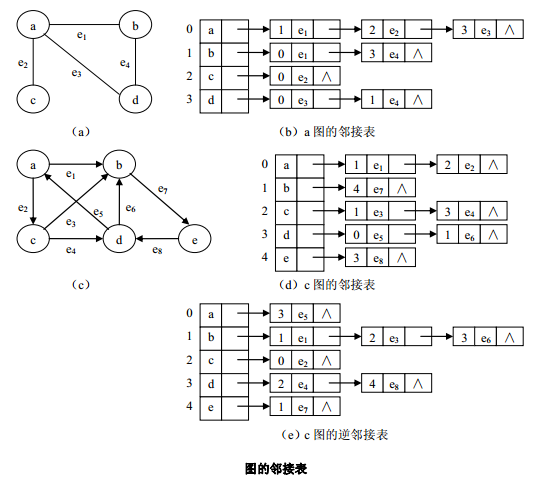
在无向图的邻接表中，顶点的每一个边表结点对应于与顶点相关联的一条边。

在有向图的邻接表中，顶点的每一个边表结点对应于以顶点为始点的一条弧，因此也称有向图的邻接表的边表为出边表。

在有向图的邻接表中，将顶点的每个边表结点对应于以顶点为重点的一条弧，即用便捷点的邻接点域存储邻接到顶点的序号，由此构成的邻接表称为有向图的逆邻接表，逆邻接表有边表称为入边表。

邻接表的性质如下：

图的邻接表表示不是惟一的，它与表结点的链入次序有关。
无向图的邻接表中第i个边表的结点个数即为第i个顶点的度。
有向图的邻接表中第i个出边表的结点个数即为第i个结点的出度，有向图的逆邻接表中第i个入边表的结点个数即为第i个结点的入度。
无向图的边数等于邻接表中边表结点数的一半，有向图的弧数等于邻接表（逆邻接表）中出边表结点（入边表结点）的数目。

需要说明的是：

在邻接表的每个线性链接表中各结点的顺序是任意的。
邻接表中的各个线性链接表不说明他们顶点之间的邻接关系。
对于无向图，某顶点的度数=该顶点对应的线性链表的结点数。
对于有向图，某顶点的“出度”数=该顶点对应的线性链表的结点数；求某顶点的“入度”需要对整个邻接表的各链接扫描一遍，看有多少与该顶点相同的结点，相同结点数之和即为“入度”值。

邻接表与邻接矩阵的关系如下：

对应于邻接矩阵的每一行有一个线形连接表；
链接表的表头对应着邻接矩阵该行的顶点；
链接表中的每个结点对应着邻接矩阵中该行的一个非零元素；
对于无向图，一个非零元素表示与该行顶点相邻接的另一个顶点；
对于有向图，非零元素则表示以该行顶点为起点的一条边的终点。

宽度（广度）优先检索BFS

广度优先搜索类似于树的层次遍历。从图中的某一顶点出发，遍历每一个顶点时，依次遍历其所有的邻接点，然后再从这些邻接点出发，同样依次访问它们的邻接点。按照此过程，直到图中所有被访问过的顶点的邻接点都被访问到。

算法实现

广度优先遍历背后基于队列，下面介绍一下具体实现的方法：

访问起始顶点，并将插入队列；
从队列中删除队头顶点，将与其相邻的未被访问的顶点插入队列中；
重复第二步，直至队列为空。

//邻接矩阵
public String breadFirstSearch(int v) {
		if (v < 0 || v >= numOfVexs)
			throw new ArrayIndexOutOfBoundsException();
		visit = new boolean[numOfVexs];
		StringBuilder sb = new StringBuilder();
		Queue<Integer> queue = new LinkedList<Integer>();
   		 queue.offer(v);
		visit[v] = true;
		while (!queue.isEmpty()) {
            v = queue.poll();
			sb.append(vexs[v] + ",");
			for (int i = 0; i < numOfVexs; i++) {
				if ((edges[v][i] != 0 && edges[v][i] != Integer.MAX_VALUE)&& !visited[i]) {
					queue.offer(i);//因为使用的是队列，所以每次poll出去的都是同一层的。这个和深度优先算法使用栈，每次pop出的都是一层中的一个元素不同
					visit[i] = true;
				}
			}
           return sb.length() > 0 ? sb.substring(0, sb.length() - 1) : null;
        }
    //邻接表
public String breadFirstSearch(int v) {
		if (v < 0 || v >= numOfVexs)
			throw new ArrayIndexOutOfBoundsException();
		visit = new boolean[numOfVexs];
		StringBuilder sb = new StringBuilder();
		Queue<Integer> queue = new LinkedList<Integer>();
		queue.offer(v);
		visit[v] = true;
		ENode current;
		while (!queue.isEmpty()) {
			v = queue.poll();
			sb.append(vexs[v].data + ",");
			current = vexs[v].firstadj;
			while (current != null) {
				if (!visited[current.adjvex]) {
					queue.offer(current.adjvex);
					visit[current.adjvex] = true;
				}
				current = current.nextadj;
			}
		}
		return sb.length() > 0 ? sb.substring(0, sb.length() - 1) : null;
}

深度优先检索DFS

从一个顶点V0开始，沿着一条路一直走到底，如果发现不能到达目标解，那就返回到上一个节点，然后从另一条路开始走到底

从图中的某一个顶点x出发，访问x，然后遍历任何一个与x相邻的未被访问的顶点y，再遍历任何一个与y相邻的未被访问的顶点z……依次类推，直到到达一个所有邻接点都被访问的顶点为止；然后，依次回退到尚有邻接点未被访问过的顶点，重复上述过程，直到图中的全部顶点都被访问过为止。

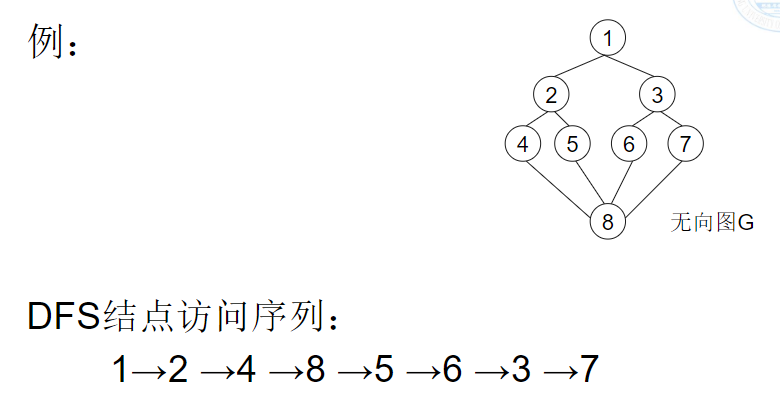
算法实现

深度优先遍历背后基于堆栈，有两种方式：第一种是在程序中显示构造堆栈，利用压栈出栈操作实现；第二种是利用递归函数调用，基于递归程序栈实现。

堆栈法

访问起始顶点，并将其压入栈中；
从栈中弹出最上面的顶点，将与其相邻的未被访问的顶点压入栈中；
重复第二步，直至栈为空栈。

//采用邻接矩阵
public void depthFirstSearch(int v) {
    if(v<0||v>=numOfVexs) throw new ArrayIndexOutOfBoundException();
    boolean []visit = new boolean[numOfVexs];//用来标记节点是否被访问
    Stack<Integer> stack  = new Stack<Integer>();
    StringBuilder sb = new StringBuilder();
    stack.push(v);
    visit[v]=true;
    while(!stack.isEmpty())
    {
        v=stack.pop();//每层依次出一个没有标记的节点
        sb.append(vexs[v] + ",");
        for(int i=numOfVexs-1;i>=0;i--)
        {
            if((edges[v][i]!=0&&edges[v][i]!=Integer.MAX_VALUE)&&!visit[i])
            {
                stack.push(i);
                visit[i]=true;
            }
        }
    }
}
//基于邻接表
public void depthFirstSearch(int v) {
   if(v<0||v>=numOfVexs) throw new ArrayIndexOutOfBoundException();
   boolean []visit = new boolean[numOfVexs];//用来标记节点是否被访问
   Stack<Integer> stack  = new Stack<Integer>();
   StringBuilder sb = new StringBuilder();
   stack.push(v);
   visit[v]=true;
	Node current;
    while(!stack.isEmpty())
    {
        v=stack.pop();//每次一层选一个出栈
        sb.append(vexs[v].data + ",");
       	current = vexs[v].firstadj;
        while(current!=null)
        {
            if(!visit[current.adjvex])
            {
                stack.push(current.adjvex);//这里也是把邻接点全部入栈
                visit[current.abjvex]=true;
            }
            current=current.nextabj;
        }
    }
}

递归法

//邻接矩阵
public void depthFirstSearch(int v) {
	if(v<0||v>=numOfVexs) throw new ArrayIndexOutOfBoundException();
	boolean []visit = new boolean[numOfVexs];//用来标记节点是否被访问
	visit[v]=true;
	printf("%d ",v);
	for(int i=0;i<numOfVexs;i++)
    {
    	if(visit[i]!=0&&(edges[v][i]!=0&&edges[v][i]!=Integer.MAX_VALUE))
    	depthFirstSearch(i);
    }
}
//邻接表
public void depthFirstSearch(int v) {
	if(v<0||v>=numOfVexs) throw new ArrayIndexOutOfBoundException();
	boolean []visit = new boolean[numOfVexs];//用来标记节点是否被访问
	visit[v]=true;
	printf("%d ",v);
    Node current;
	while(current!=null)
    {
        if(visit[current.abjvex]!=true)
            depthFirstSearch(current.abjvex);
                    current=current.nextabj;
    }
}

rhb_blog

基本的图算法

图检索算法

图的表示

邻接矩阵

邻接表

宽度（广度）优先检索BFS

算法实现

深度优先检索DFS

算法实现

堆栈法

递归法