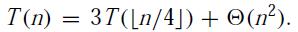分治策略

分治法遵循三个基本步骤：

1）分解（Divide）：将原问题分为若干个规模较小、相互独立，性质与原问题一样的子问题；

2）解决（Conquer）：若子问题规模较小、可直接求解时则直接解；否则“递归”求解各个子问题，即继续将较大子问题分解为更小的子问题，然后用同一策略继续求解子问题。

3）合并（Combine）：将子问题的解合并成原问题的解。

递归式求解的三种方法

通常遇到的输入规模为n的递归式，形式如下：

$$T(n) = aT(n/b) + f(n)$$

该式描述的是：它将规模为n的问题分解为a个子问题，每个子问题规模为n/b，其中a和b都是正常数。a个子问题递归地进行求解，每个花费时间T(n/b)。函数f(n)包含了问题分解和子问题解合并的代价。例如，描述Strassen算法的递归式中，a=7，b=2，f(n) = Θ(n2) 。

接下来分析求解上述式子的三种方法

代入法

实质上就是数学归纳法，先对一个小的值做假设，然后推测更大的值得正确性。

​ 1.猜测解的形式；

​ 2.用数学归纳法求出解中的常数，并证明解是正确的。

示例

T(n) = 2T(n/2) + n

• step one: 猜测
  上述等式可以转换为 T(n)/n = 2T(n/2)/n + 1
  令 S(n) = T(n)/n
  则S(n) = S(n/2) + 1
  而这种形式与以下的等式很像(这是关键步骤)
  lgn = lg (n/2) + 1 (此处lg2 = 1)
  因此可以推测 T(n) / n = clgn (c是常数)

因此猜出其解为 T(n) = O(nlgn)

• step two: 数学归纳法证明这个解的合理性
  直接代入去运算

递归树法

利用递归树方法求算法复杂度，其实是提供了一个好的猜测，简单而直观。在递归树中，每一个结点表示一个单一问题的代价，子问题对应某次递归函数调用。我们将树中每层中的代价求和，得到每层代价，然后将所有层的代价求和，得到所有层次的递归调用总代价。简单来说就是将递归的一层一层分析出来，再累加求和。

递归树最适合用来生成好的猜测，然后可用代入法来验证猜测是否正确。当使用递归树来生成好的猜测时，常常要忍受一点儿“不精确”，因为关注的是如何寻找解的一个上界。

示例

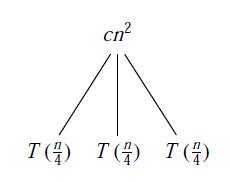
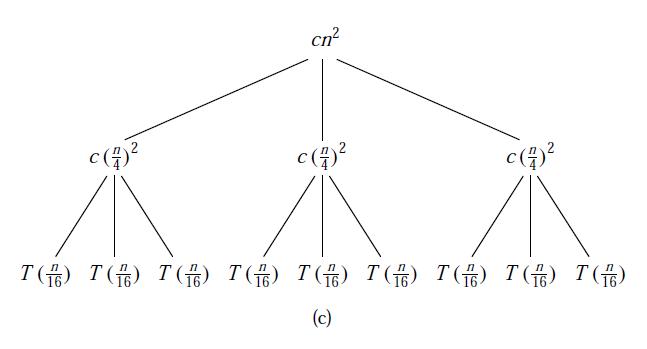
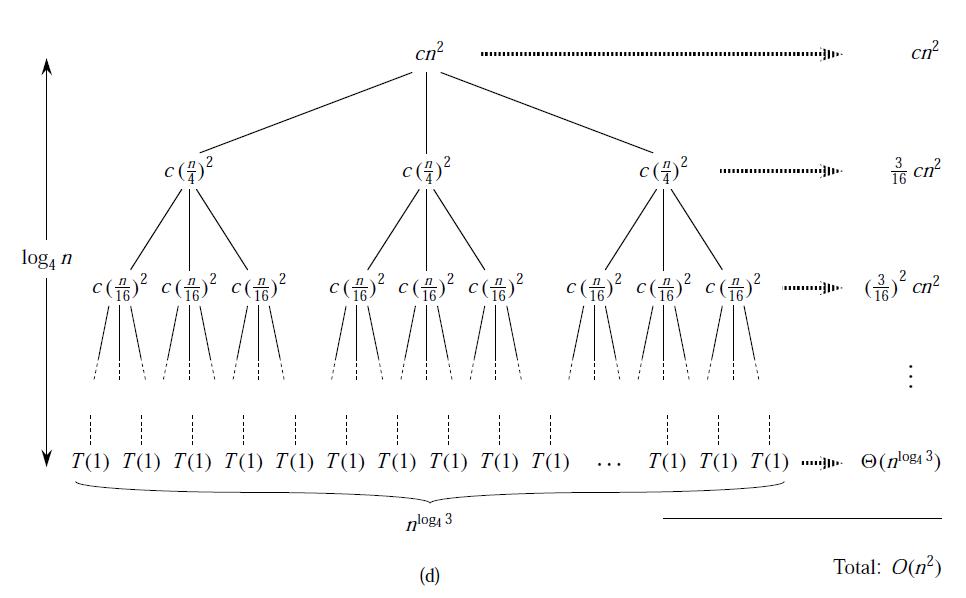
在递归树中，每一个结点都代表一个子代价，每层的代价是该层所有子代价的总和，总问题的代价就是所有层的代价总和。所以，我们利用递归树求解代价，只要知道每一层的代价和层数即可。

这些，都需要直观的找出规律，以上图为例，当递归调用到叶子T(1)时所用到的递归次数就是整棵递归树的深度。我们从图中可以得到第i层的结点的代价为n/(4^i)，当n/(4^i)=1即i = log4(n)时，递归到达了叶子，故整棵递归树的深度为log4(n)。总代价是所有层代价的总和。

主方法（最普适）

定理4.1（主定理） 令 a≥1 和 b>1 是常数，f(n) 是一个函数，T(n) 是定义在非负整数上的递归式：
$T(n) = aT(n/b) + f(n)$
那么T(n)有如下渐进界：

1. 若对某个常数 ε>0 有 f(n) = O(nlogb^a^-ε)，则 T(n) = Θ(nlogb^a^) 。
2. 若 f(n) = Θ(nlogba)，则 T(n) = Θ(nlogb^a^lgn) 。
3. 若对某个常数 ε>0 有 f(n) = Ω(nlogb^a^+ε)，且**对某个常数 c<1 和所有足够大的 n 有 af(n/b) ≤ cf(n)**，则 T(n) = Θ(f(n)) 。

将余项f(n)与函数 nlogb^a^ 进行比较， 直觉上来说两个函数的较大者决定了递归式的解，如情况一是 nlogba 较大，情况3是 f(n) 较大。而情况2是两者一样大，这种情况需要乘上一个对数因子。

这里要注意主方法不能求解的地方，所有的大于和小于都是多项式意义上的大于和小于，对于有些递归式夹在三种情况的间隙中，是无法用主方法来求解的。下面解释一下什么是多项式意义上的小于和大于：

f(x)多项式大于g(x):存在实数e>0,使得f(x)>g(x)n^e^
f(x)多项式小于g(x):存在实数e>0,使得f(x)<g(x)n^e^

举个例子，有递归式T(n) = 2T(n/2)+nlgn。

对于这个递归式，我们有 a = 2，b = 2， f(n) = n，因此 nlogb^a^ = nlog2^2^ = Θ(n^1^) 。

但是nlogn仅仅渐进大于n

因为对于任意c>0,均有logn < n^c^(由洛必达法则可知)。

示例

T(n) = 9T(n/3) + n

对于这个递归式，我们有 a = 9，b = 3， f(n) = n，因此 nlogb^a^ = nlog3^9^ = Θ(n^2^) 。而 f(n) = n 渐进小于 Θ(n^2^)，所以可以应用于主定理的情况1，从而得到解 T(n) = Θ(n^2^) 。

T(n) = T(2n/3) + 1

其中，a = 1， b = 3/2， f(n) = 1，因此 nlogb^a^ = nlog3/2^1^ = n^0^ = 1 。由于 f(n) = Θ(1) ，与Θ(nlogb^a^)恰好相等，可应用于情况2，从而得到解 T(n) = Θ(lgn) 。

T(n) = 3T(n/4) + nlgn

我们有 a = 3，b = 4，f(n) = nlgn，因此nlogb^a^ = nlog4^3^ = O(n^0.793^) 。由于 f(n) = Θ(nlgn) = Ω(n) = Ω(n^0.793+0.207^)，因此可以考虑应用于情况3，其中 ε = 0.207。但需要检查是否满足条件：当 n 足够大时，存在 c<1 使 af(n/b) ≤ cf(n) 。

• 令 3f(n/4) ≤ cf(n) 有
  3n/4lg(n/4) ≤ cnlgn
  3/4(lgn - lg4) ≤ clgn
  (3/4 - c)lgn ≤ 3/4lg4

容易发现，当 c ≥ 3/4 时，上式对于足够大的 n 恒成立。因此可以使用主定理的情况3，得出递归式的解为 T(n) = Θ(nlgn) 。

最大子数组问题

已知数组A，在A中寻找“和最大”的非空连续子数组。——称这样的连续子数组为最大子数组(maximum subarray)

方法一：暴力求解

暴力求解的时间复杂度为O（n^2^）

方法二：分治求解

分治求解的核心在于递归。所以需要考虑最大子数组如何满足递归的要求。

首先，将数组分成均分为两个部分。那么最大子数组可能存在的位置可能存在的情况有三种：

1. 最大子数组在左边的数组中
2. 最大子数组在右边数组中
3. 最大子数组跨越了左右两个子数组

递归的结束：左右子数组的元素为1时，就可以结束递归了。

递归层需要做的事情：计算左右子数组的最大子数组和横跨左右子数组的最大数组。
在求解横跨左右子数组的最大数组时，可以从mid出发，分别向左和向右找出“和最大”的子区间，mid分别是左右区间的终点和起点。然后合并这两个区间即可得到跨越中点时的A[low … high]的最大子数组。

递归的返回值：返回MAX（左右子数组的最大子数组，横跨左右子数组的最大数组）

性能分析

对A[low..mid]和A[mid+1..high]两个子问题递归求解，每个子问题的规模是n/2，所以每个子问题的求解时间为T(n/2)，两个子问题递归求解的总时间是2T(n/2)。

FIND-MAX-CROSSING-SUBARRAY的时间是Θ(n)。

所以T(n)=Θ(nlgn）

示例

Leetcode 53.最大子序和

class Solution {
    public int maxSubArray(int[] nums) {
        int l = nums.length;
        if(l==0)
        return 0;
        return maxSubArraySum(nums,0,l-1);
    }
    public int maxSubArraySum(int[] nums,int l,int r)
    {
        
        //递归的结束：当只有子数组只有一个元素的时候
        if(l==r)
        return nums[l];
        int mid=(r+l)/2;
        int temp  = Math.max(maxSubArraySum(nums,mid+1,r),maxCrossingSum(nums,l,mid,r));
        return Math.max(maxSubArraySum(nums,l,mid),temp);
    }
    public int maxCrossingSum(int[] nums,int l,int mid ,int r)
    {
        int sum=0;
        int leftsum=Integer.MIN_VALUE;
        //从mid的左边走，一直走到最大子数组的位置
        for(int i=mid;i>=l;i--)
        {
            sum+=nums[i];
            if(sum>=leftsum)
            leftsum=sum;
        }
        sum=0;
        int rightsum=Integer.MIN_VALUE;
        for(int i=mid+1;i<=r;i++)
        {
            sum+=nums[i];
            if(sum>rightsum)
            rightsum=sum;
        }
        return leftsum+rightsum;
    }
}

Strassen矩阵乘法

矩阵乘法是种极其耗时的运算。

以C = A • B为例，其中A和B都是 n x n 的矩阵。根据矩阵乘法的定义，计算过程如下：

SQUARE-MATRIX-MULTIPLY(A, B)
n = A.rows
let C be a new nxn matrix
for i = 1 to n
    for j = 1 to n
        c[i][j] = 0
        for k = 1 to n
            c[i][j] += a[i][k] * b[k][j]
return C

由于存在三层循环，它的时间复杂度将达到O(n3)。

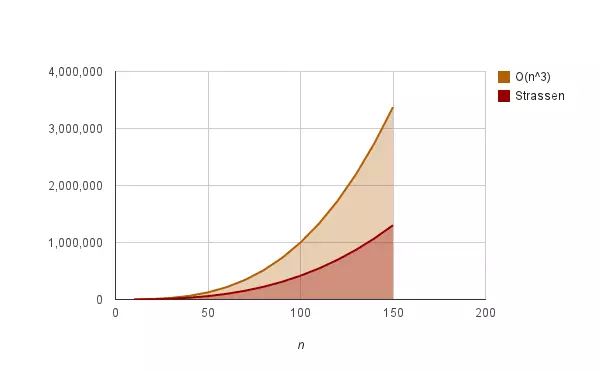
这是一个很可怕的数字。但是，凭着科学家们的智慧，这个数正在一步步下降。本文介绍经典的Strassen算法，该算法将时间复杂度降低到O(nlg7) ≈ O(n2.81)。别小看这个细微的改进，当n非常大时，该算法将比平凡算法节约大量时间。

分治法

Strassen算法基于分治的思想，因此我们首先考虑一个简单的分治策略。

每个 n x n 的矩阵都可以分割为四个 n/2 x n/2 的矩阵：

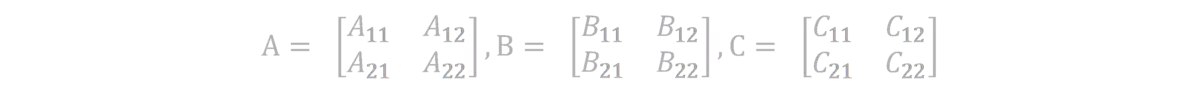
因此可以将公式C = A • B改写为

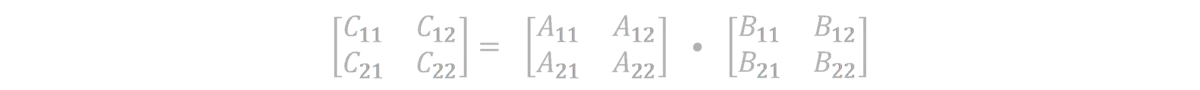
于是上式就等价于如下四个公式：

（式3-3）
C11 = A11 • B11 + A12 • B21
C12 = A11 • B12 + A12 • B22
C21 = A21 • B11 + A22 • B21
C22 = A21 • B12 + A22 • B22

注：任意两个子矩阵块的乘可以沿用同样的规则：如果子矩阵的阶大于2，则将子矩阵分成更小的子矩阵，直到每个子矩阵只含一个元素为止。从而构造出一个递归计算过程。

每个公式需要计算两次矩阵乘法和一次矩阵加法，使用T(n)表示 n x n 矩阵乘法的时间复杂度，那么我们可以根据上面的分解得到一个递推公式。

T(n) = 8T(n/2) + Θ(n^2^)

其中，8T(n/2)表示8次矩阵乘法，而且相乘的矩阵规模降到了n/2。Θ(n^2^)表示4次矩阵加法的时间复杂度以及合并C矩阵的时间复杂度。

要想计算出T(n)并不复杂，可以采用画递归树的方式计算，结果是T(n) = Θ(n^3^)

可见，简单的分治策略并没有起到加速运算的效果。

Strassen算法

让我们回头观察前面使用分治策略的时候为什么无法提高速度。

因为分解后的问题包含了8次矩阵相乘和4次矩阵相加，就是这8次矩阵相乘导致了速度不能提升。于是我们想到能不能减少矩阵相乘的次数，取而代之的是矩阵相加的次数增加。Strassen正是利用了这一点。

现在，我们来看一下Strassen算法的原理。

仍然把每个矩阵分割为4份，然后创建如下10个中间矩阵：

S1 = B12 - B22
S2 = A11 + A12
S3 = A21 + A22
S4 = B21 - B11
S5 = A11 + A22
S6 = B11 + B22
S7 = A12 - A22
S8 = B21 + B22
S9 = A11 - A21
S10 = B11 + B12

接着，计算7次矩阵乘法：

P1 = A11 • S1
P2 = S2 • B22
P3 = S3 • B11
P4 = A22 • S4
P5 = S5 • S6
P6 = S7 • S8
P7 = S9 • S10

最后，根据这7个结果就可以计算出C矩阵：
C11 = P5 + P4 - P2 + P6
C12 = P1 + P2
C21 = P3 + P4
C22 = P5 + P1 - P3 - P7

我们可以把P矩阵和S矩阵展开，并带入最后的式子计算，会发现恰好是公式3中的四个式子。也就是说，Strassen为了计算公式3，绕了一大圈，用了更多的步骤，成功的把计算量变成了7个矩阵乘法和18个矩阵加法。虽然矩阵加法增加了好几倍，而矩阵乘法只减小了1个，但在数量级面前，18个加法仍然渐进快于1个乘法。这就是该算法的精妙之处。

同样地，我们可以写出Strassen算法的递推公式：

T(n) = 7T(n/2) + Θ(n2)

使用递归树或主方法可以计算出结果：

T(n) = Θ(nlg7) ≈ Θ(n2.81)

下图展示了平凡算法和Strassen算法的性能差异，n越大，Strassen算法节约的时间越多。

最近点对问题