概叙
术语说明:
- 稳定 :如果a原本在b前面,而a=b,排序之后a仍然在b的前面;
- 不稳定 :如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面;
- 内排序 :所有排序操作都在内存中完成;
- 外排序 :由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
当n较大,则应采用时间复杂度为O(nlog2n)的排序方法:快速排序、堆排序或归并排序。
快速排序:是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;
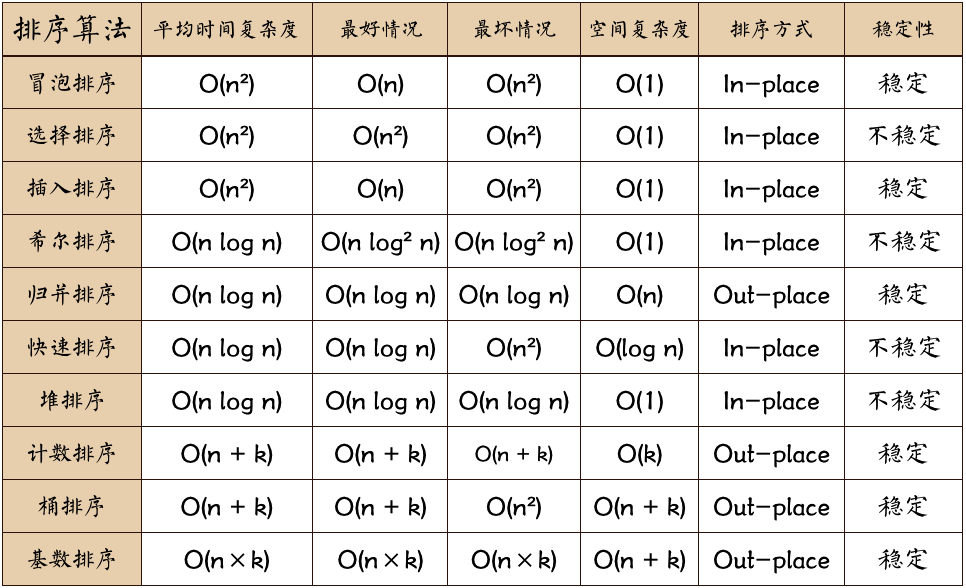
1.插入排序—直接插入排序(Straight Insertion Sort)
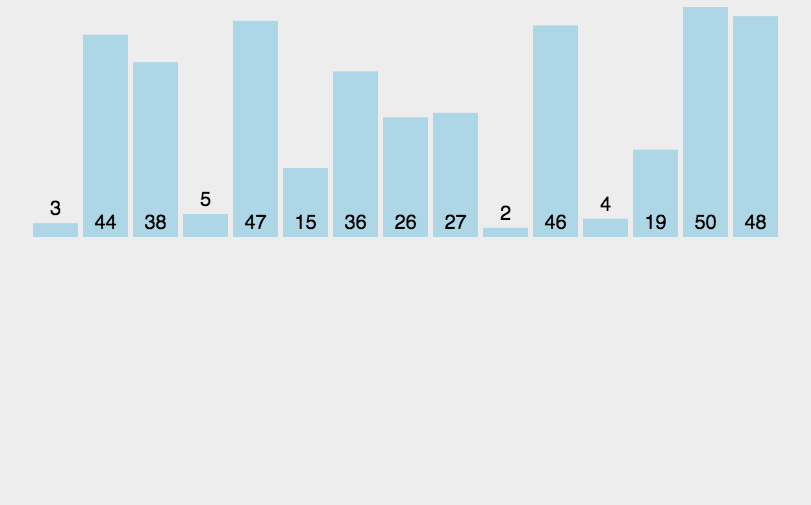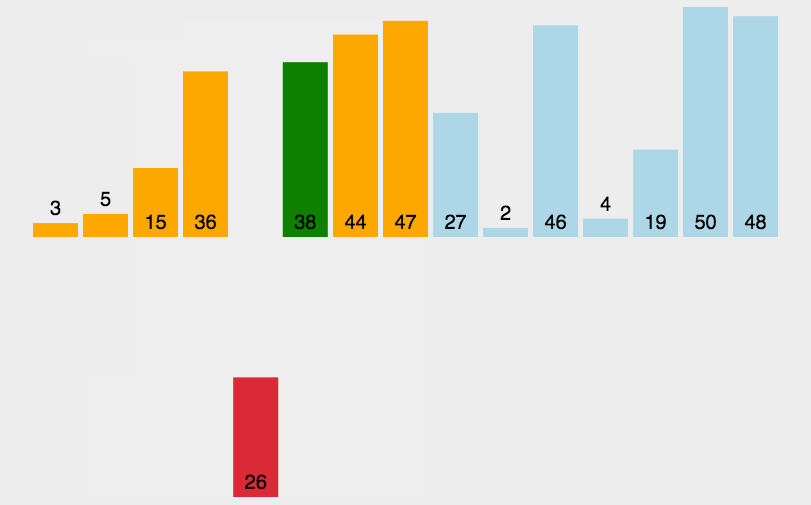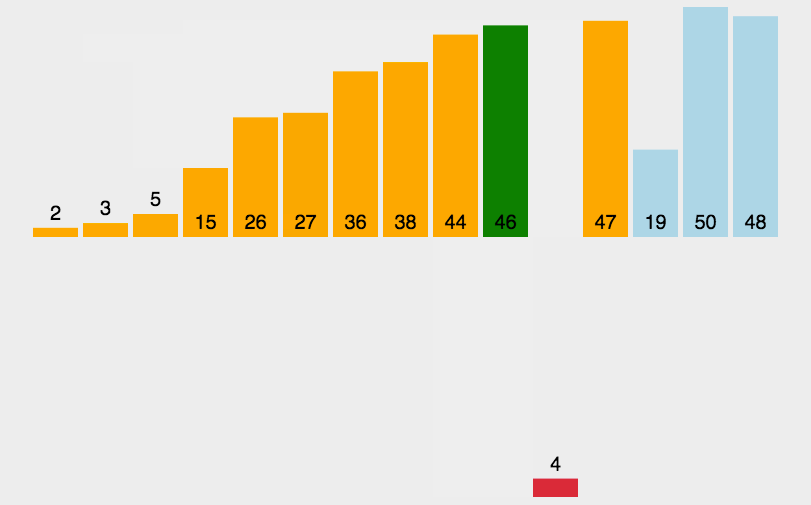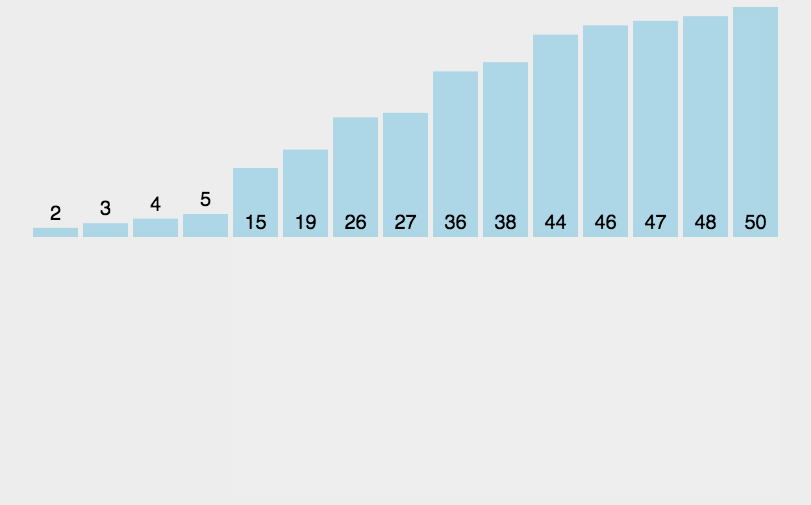
插入排序简单来说就是不断从后面将数据插入前面已经排好序的过程。
由此可知:前面的队列一定是排好序的。在插入的过程中可能会导致前面排好序的数据往后移,腾出位置。
动画演示:
2.归并排序(Merge Sort)
简单来说,归并排序就是将一个无序的序列分解成诺干个有序的子序列,然后依次归并。
一般采取的是递归的方式进行设计。
递归的结束标志是:当分解的序列只有一个元素时。
递归层需要做的是:将子序列排序。
递归层返回的是:排好序的子序列
递归请见:
动画演示:
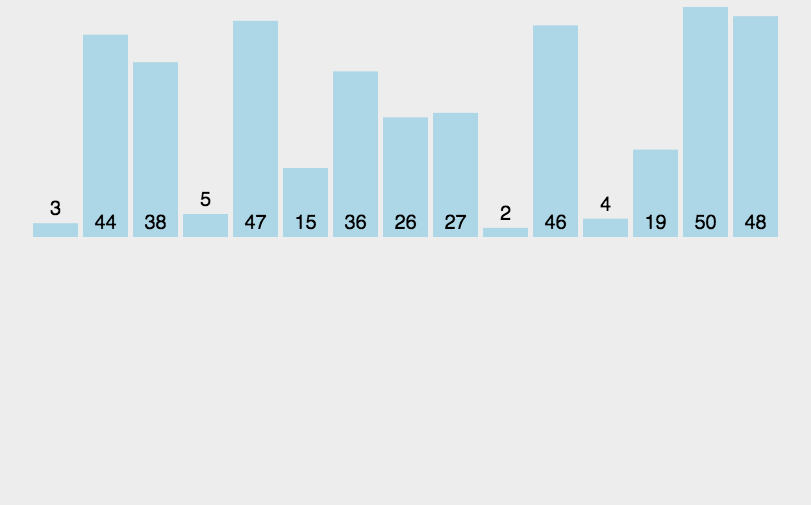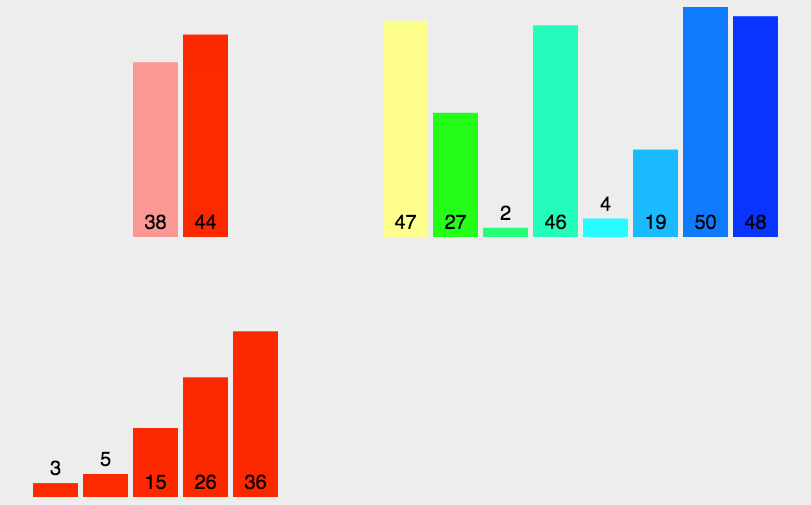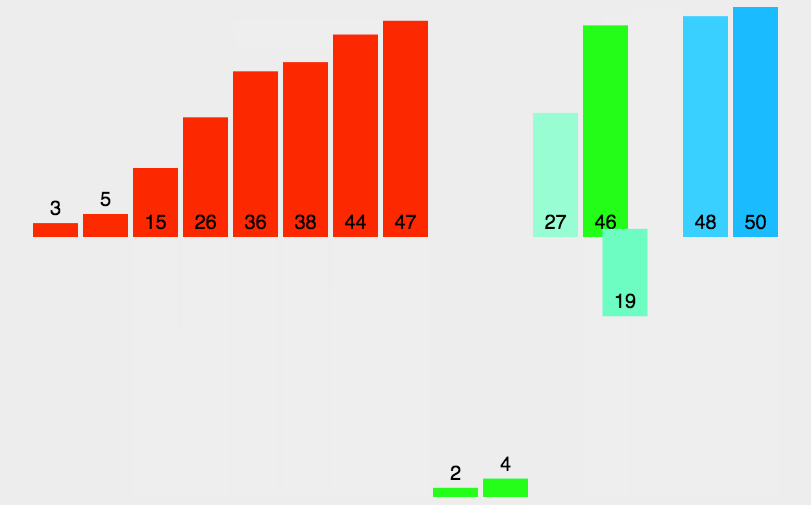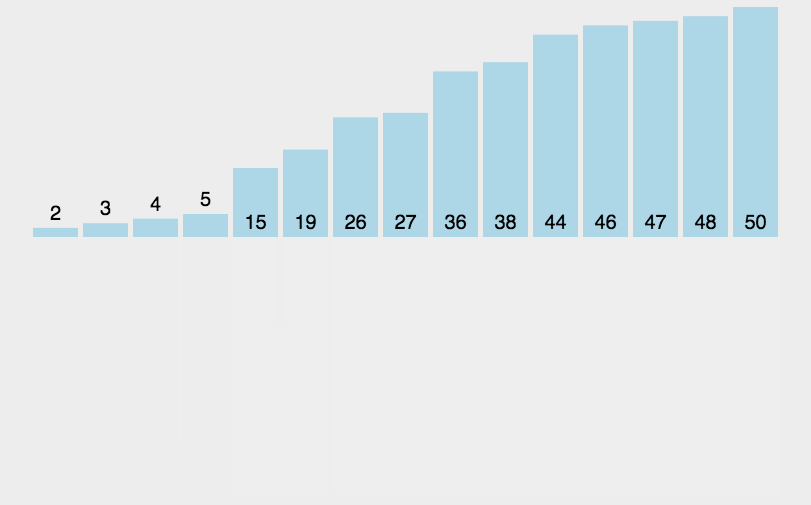
看不明白?再看一个。
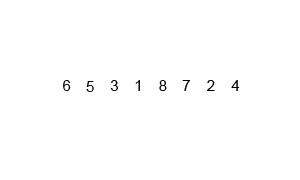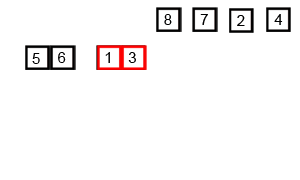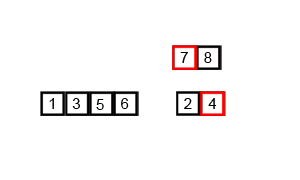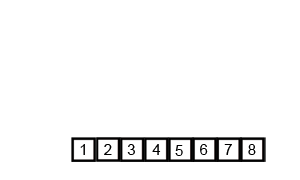
3、堆排序(Heap Sort)
堆排序(Heapsort) 是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
- 算法描述
- 步骤1:将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
- 步骤2:将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
- 步骤3:由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
- 演示

算法分析
- 最佳情况:T(n) = O(nlogn)
- 最差情况:T(n) = O(nlogn)
- 平均情况:T(n) = O(nlogn)
4、快速排序(Quick Sort)
快速排序 的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
算法描述
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
- 步骤1:从数列中挑出一个元素,称为 “基准”(pivot );
- 步骤2:重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 步骤3:递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
示例
概括来说为 挖坑填数+分治法
下面举例来进行说明,主要有三个参数,i为区间的开始地址,j为区间的结束地址,X为当前的开始的值
第一步,i=0,j=9,X=72(X可以理解成此时a[0]是挖了一个洞,东西放在X哪里。这个洞可以填入其他数据)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 72 | 6 | 57 | 88 | 60 | 42 | 83 | 73 | 48 | 85 |
第二步,从j开始由后向前找,找到比X小的第一个数a[8]=48,此时:a[0]=a[8];i++
进行替换。这样a[0]这个坑被填上了,但是a[7]这个坑多出来了。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 48 | 6 | 57 | 88 | 60 | 42 | 83 | 73 | 72 | 85 |
第三步,从i开始由前往后找,找到比X大的第一个数a[3]=88,(此处找比X大的数是因为在后半截的数据均要比72才算实现目的)此时:a[8]=a[3];j–
a[8]的坑被填上了,但是a[3]的坑又出现了。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 48 | 6 | 57 | 88 | 60 | 42 | 83 | 73 | 88 | 85 |
此时:i=3;j=7;X=72(因为经过上几轮的比较,我们可以得出前3个数均比72小,后3个数都比72大,不予考虑)
再重复上面的步骤,先从后向前找,再从前向后找。
第四步,从j=7开始由后向前找,找到比X小的第一个数a[5]=42,a[3] = a[5]; i++;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 48 | 6 | 57 | 42 | 60 | 42 | 83 | 73 | 88 | 85 |
第五步,从i=5开始由前往后找,i=j=5,所以退出,将X填入a[5]
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 48 | 6 | 57 | 42 | 60 | 72 | 83 | 73 | 88 | 85 |
一轮结束。
接下来对两个子区间[0,4]和[6,9]重复上面的操作即可
总结:
1.i =L; j = R; 将基准数挖出形成第一个坑a[i]。
2.j–由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中。
3.i++由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中。
4.再重复执行2,3二步,直到i==j,将基准数填入a[i]中
- 动图演示
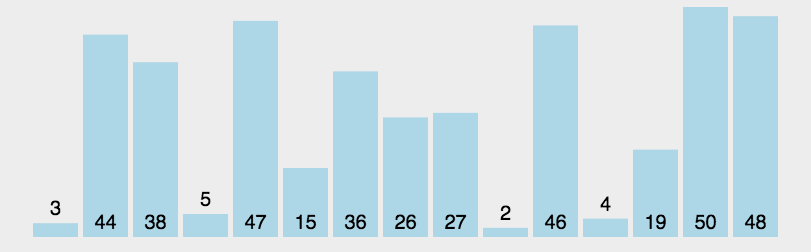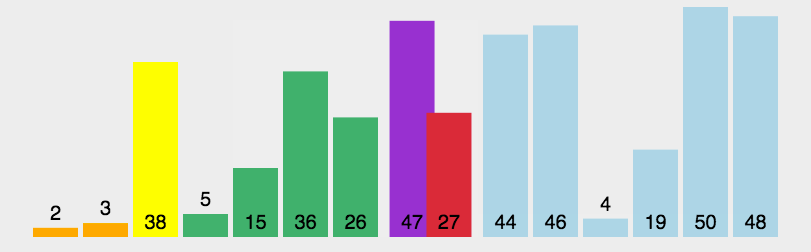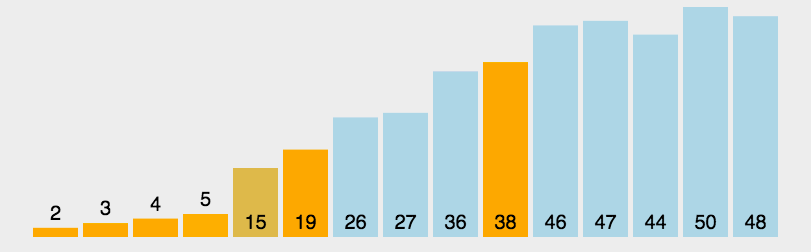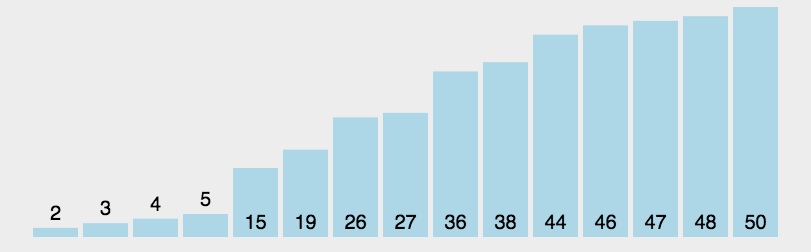
算法分析
- 最佳情况:T(n) = O(nlogn)
- 最差情况:T(n) = O(n2)
- 平均情况:T(n) = O(nlogn)
排序算法的下界
排序,涉及到被排序的序列和排序的方法。(比较)排序算法时间的下界对被排序的序列和排序方法做了以下限制
没有关于被排序序列的先验信息,譬如序列内数据的分布、范围等,即认为序列内元素在一个开区间内均匀分布。同时,序列内元素互异。(可以从两个方面理解元素互异的限制,其一是对于随机的序列而言,两元素相同的概率约为0;其二是比较排序中没有对相同元素的特殊处理)
排序方法中仅仅利用了比较运算来确定元素的顺序。不失一般性,假设每次比较仅取2个元素,比较其大小。
(比较)排序算法的算法时间复杂度等价为确定输入序列的排列方式需要多少次比较操作。
选择,插入,归并,快速排序算法,在确定排序顺序时都仅仅依赖于对排序关键字对进行比较,它们确定决策时的依据均是”如果这个元素的排序关键字比另一个元素的排序关键字小,那么就进行相应操作,否则,进行其他操作或者什么也不做”,这些排序算法就是比较排序。
基于比较排序的下界
将比较排序定义为仅仅通过比较元素对来确定排序顺序,
Ω符号给出了下界,因此称“对于任意大的n,任何比较排序算法在最坏情况下至少需要cnlgn次比较操作(对于某个常量c成立)”由于每次比较至少需要花费常量时间,对于n个元素的基于比较的排序操作,能够得出一个时间为Ω(nlgn)的下界。
关于此下界的说明:
1.它仅仅指最坏情况。在最坏情况下,该排序必定需要Ω(nlgn)次比较操作。
2.Ω(nlgn)这一下界不依赖于任何算法,只要该算法是一个比较排序。
决策二叉树
决策树:用于证明排序算法的下界,是一个二叉树,每个节点是元素之间一组可能的排序,比较的结果是树的边,下图表示将a,b,c排序的算法
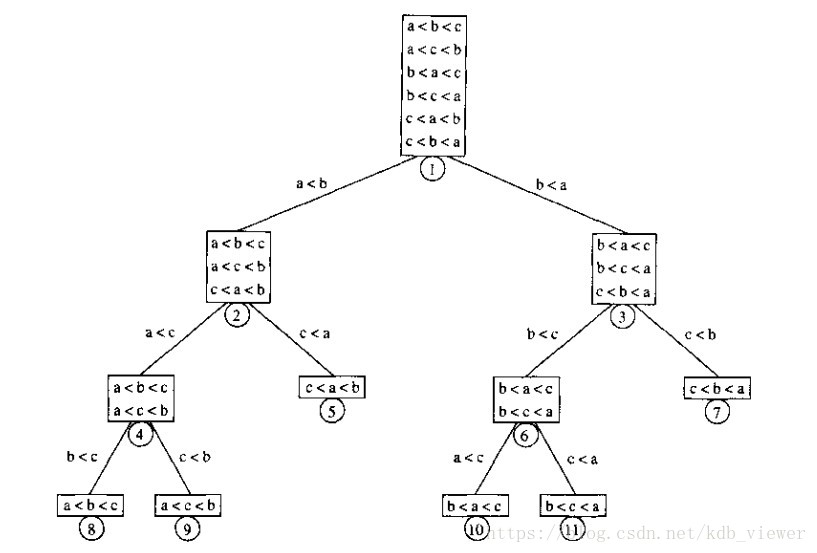
定理:任何只用到比较的算法最坏情况下需要Ω(nlgn)次比较!!
证明:假设高度为h,具有l个可达叶结点的决策树。输入n!种可能的排列都是叶结点,所以n!<=l。且l<=2^h^
两边取对数即可得证。
推论:堆排序和归并排序都是渐近最优的比较排序算法
以比较为基础的有序检索算法最坏情况下的时间下界:
定理 :设A(1:n)含有n(n≥1)个不同的元素,且有A(1) < A(2) < …< A(n)。
以以比较为基础的算法去判断给定的x是否有,则,最坏情况下,任何这样的算法所需的最小比较次数FIND(n)有:
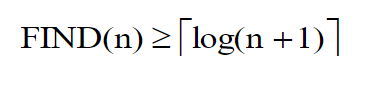
1)任何一种以比较为基础的有序检索算法,在最坏情况下的计算时间都不低于Ο(logn)。因此,不可能存在最坏情况比二分检索数量级还低的算法。
2)二分检索是解决检索问题的最优的最坏情况算法
参考文章:https://blog.csdn.net/MobiusStrip/article/details/83785159