运算方法和运算器
定点数运算及溢出检测
在机器当中采用补码进行运算。
补码加法:[X+Y]补= [X]补+[Y]补 (mod M)
补码减法:[X−Y]补 = [X]补+[−Y]补 = [X]补−[Y]补
1、这就意味着对所有的数进行运算,都要将其变成补码的形式后再进行运算。
2、得到的答案也是补码,再进行补码转原码。
在硬件的角度考虑:要想使用加法器去实现减法操作,就需要求出[−Y]补
求补公式:[−Y]补= [ [Y]补 ]补
数溢出的概念及其判断方法
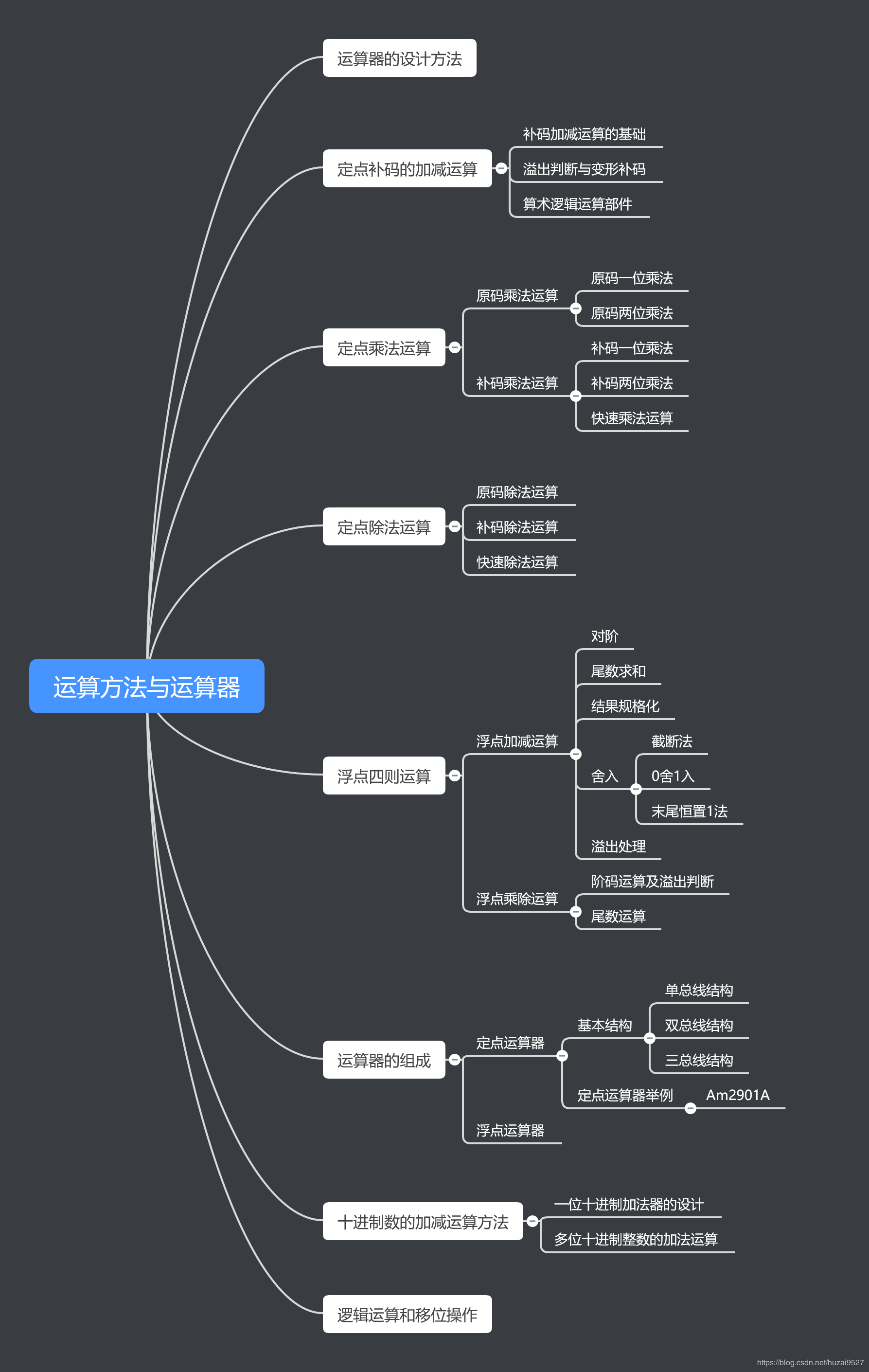
溢出:运算结果超出了某种数据类型的表示范围。
溢出和进位的区别:
- 溢出是错误,进位不是错误(进位是在运算范围内!溢出就是计算错误)
- 溢出是有符号数相加发生的错误: 如 两个正数相加=负数,两个负数相加=正数; 进位是无符号数运算结果超出范围。
溢出是针对有符号数而言的。只有当正+正=负或者负+负=正的时候就表示溢出。如两个操作数符号相同而运算结果的符号与之相反时OV(溢出位)=1,反之,OV=0。
进位是针对无符号数而言的。它的进位就相当于有符号数中的溢出.
通俗一点说就是,即使有符号数相加/相减导致了CF=1也没什么意义,不能说明结果的正确与否。
1、CF的判断
①加法
十进制角度,如果两无符号数相加,结果大于2^n^-1(n为位数),则CF=1,否则CF=0;
二进制角度,如果两无符号数相加,最高位向前有进位,则CF=1,否则CF=0。
②减法
十进制角度,如果两无符号数相减,减数大于被减数(也即结果不在0—2^n^-1内),则CF=1,否则CF=0;
二进制角度,如果两无符号数相减,最高位向前游借位,则CF=1,否则CF=0。
2、OF的判断
①加法
十进制角度,如果两有符号数相加,结果不在-2^(n-1)~2^(n-1)-1内,则OF=1,否则OF=0;
二进制角度,如果两有符号数同号,而相加结果与之异号,则OF=1,否则OF=0。
②减法
十进制角度,如果有符号数相减结果在-2^(n-1)~2^(n-1)-1内,则OF=1,否则OF=0;
二进制角度,如果两个数异号,而相减结果与被减数符号相反,则OF=1,否则OF=0。
溢出的检测:
1、对操作数和运算结果的符号进行检测:正+正的运算结果的符号位一定是正
2、对最高数据位进位和符号位进位进行检测:
正+正的符号位不进位,但是当最高位数据位进位的时候就会顶到符号位上。
负+负的符号位进位,当最高位数据位进位恰好把符号位修改回来。但是最高位数据位不进位就会导致符号位错误。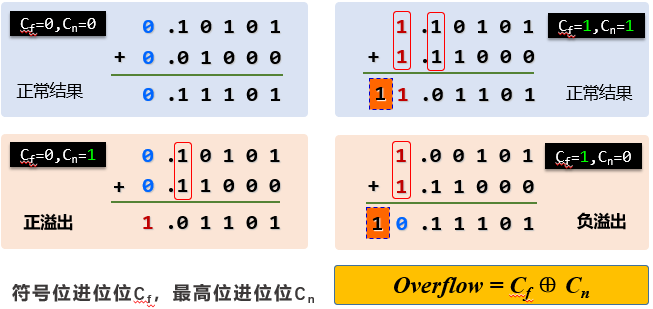
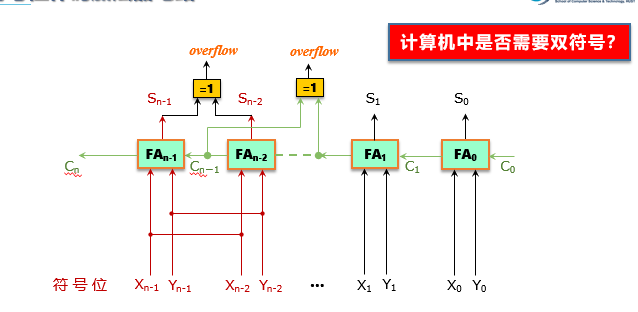
双符号位的溢出检测:
3、变形补码(也叫模4补码):把两个数的符号位放在一起,即每个参与运算的数据都有两个符号位(00表示正数、11表示负数)
一个符号位只能表示正、负两种情况,当产生溢出时,符号位的含义就会发生混乱。如果将符号位扩充为两位,其所能表示的信息量将随之扩大,既能检测是否溢出,又能指出结果的符号。在双符号位的情况下,把左边的符号位叫做真符因为它代表了该数真正的符号,两个符号位都作为数的一部分参加运算。这种编码又称为变形补码。
双符号位的含义如下:
- S1S2=00 结果为正数,无溢出
- S1S2=01 结果正溢
- S1S2=10 结果负溢
- S1S2=11 结果为负数,无溢出

无符号数运算的溢出判断(其实是没有溢出的问题,就是借位的问题)
1、无符号数加法的溢出可用ALU的进位表示
2、无符号数减法的溢出可用带加/减功能的ALU的进位取反后表示(意思是向最高位的上一位借位)
定点数补码加、减运算器设计
补码串行加法器
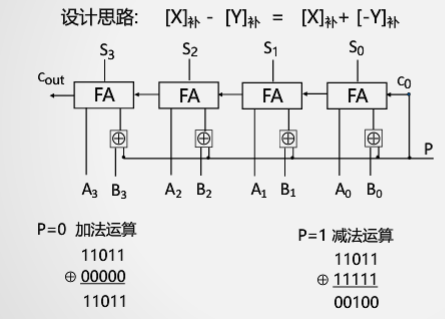
有符号溢出检测方是中第一种:正+正=负
有符号溢出检测方法是第二种:符号位进位和最高位进位异或
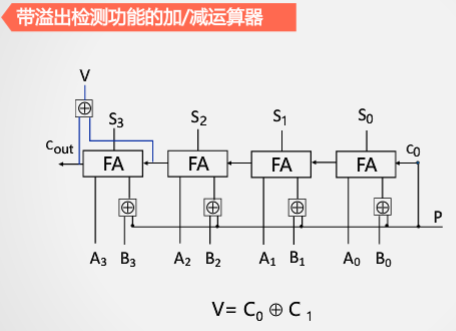
有符号溢出检测是第三种:双符号位
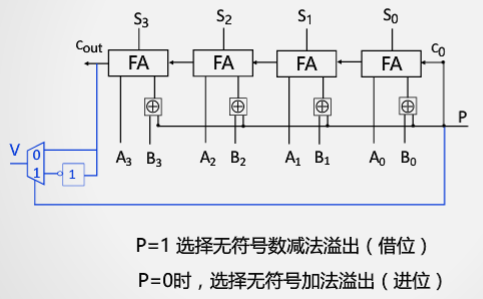
无符号溢出检测:无符号溢出就是数据放不下,故这里需要考虑的是最高位的进位
思考:有符号和无符号加法器有什么区别?
A:无符号加减法不存在溢出问题,只是将进位或借位存储在CF中。
机器不知道你进行的运算是否有符号,如果你进行的是有符号运算,你需要查看OF,否则不需要。
所以,溢出不溢出,是由程序员判断的,机器不知道。
但是无符号的“溢出”和有符号的不一样。
串行进位的效率
要等前一个数的进位。
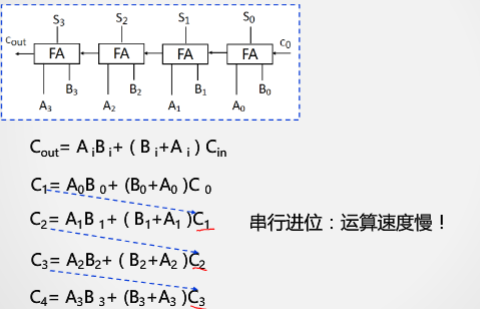
串行加法器的时间延迟
n个全加器延迟,考虑片内并行性,2n+1个门电路延迟。(一个全加器是3个门电路延迟)
并行进位加法器
把串行进位的进位位带入,就可以消除串行进位的进位位要等待的时间。加快运算

然后将带入的算式添加到并行进位运算器中:

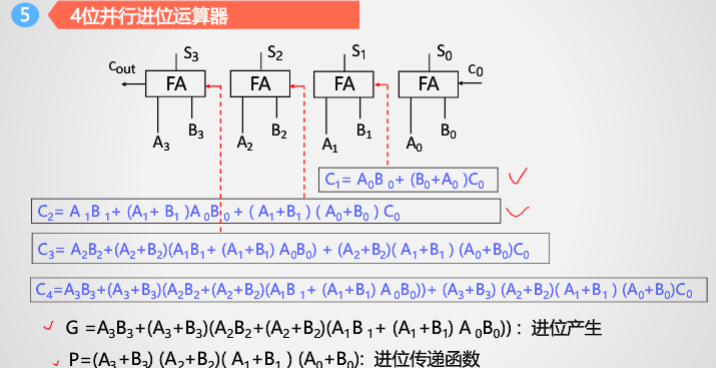
将多个并行加法器连接在一起,构建多位串行进位的并行进位加法器
将多位数的数据拆分,并行进行加法:A15-12等
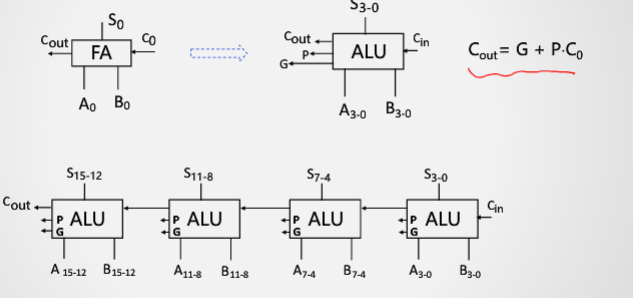
但是,这样存在一个问题:依旧需要串行等待。仿照上述方法,将进位打破
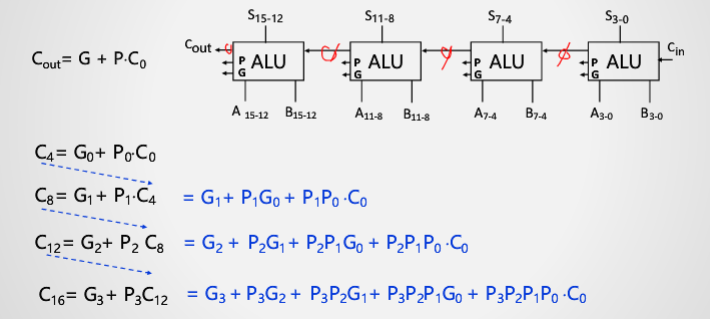
进行到这一步。只需要将P1到P3和G1到G3的值计算得到,就可以完全进行并行进位。
于是,得到的电路图为:
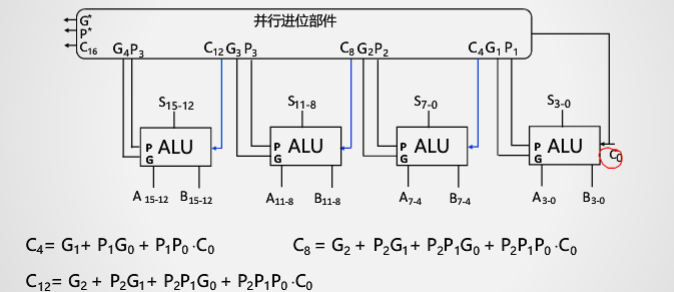
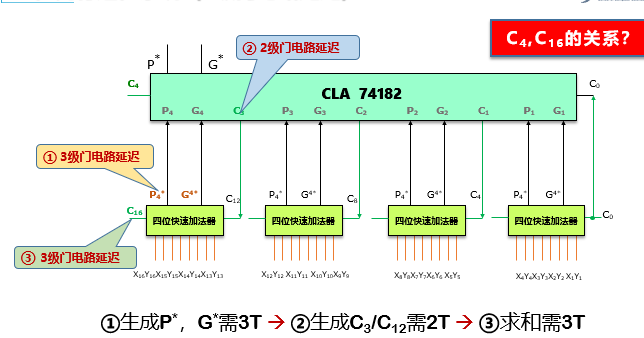
电路延迟示例
16位先行进位系统(8级门电路延迟)
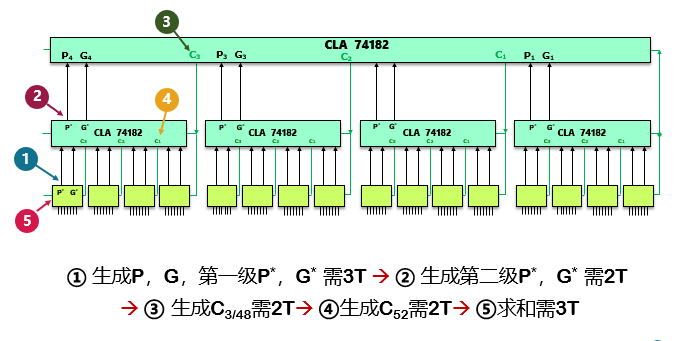
64位先行进位系统(12级门电路延迟)
原码一位乘法
移位
只针对补码而言
**算术左移和逻辑左移的效果是一样的,效果都是*2
逻辑右移最高位补0,算术右移最高位补符号位.**算术右移的效果是/2
逻辑左移=算数左移,右边统一添0
逻辑右移,左边统一添0
算数右移,左边添加的数和符号有关
设计


从手工计算的二进制乘法,可以得到最右边一位是可以直接输出的,故可以每次左移一位,输出的最右边的一位放置在乘法数上(因为0.101在1进行乘法运算后就没用了,可以移动为00.10,于是最左边的0可以用来放置FA循环累加的部分积—最右边的数0)
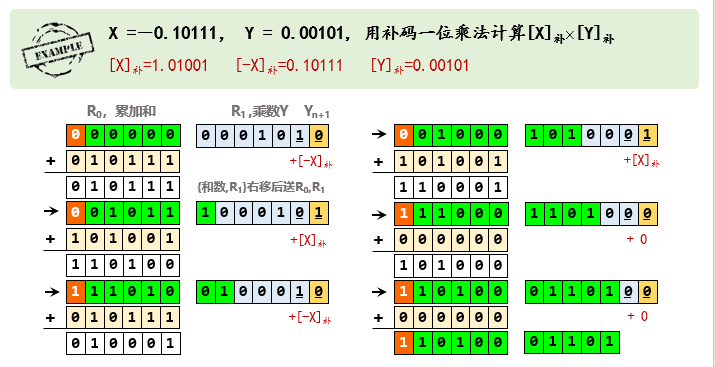
补码一位乘法
补码和真值的转换公式
$$
设[X]补=X_0.X_1X_2……X_n\
当X>=0,X_0=0,[X]补=0.X_1X_2……X_n=\sum{i=1}^{n}X_i2^{-i}=X\
当X<0,X_0=1,[X]补=1.X_1X_2……X_n=2+X\
所以:\
X=1.X_1X_2……X_n-2=-1+0.X_1X_2……X_n=-1+\sum{i=1}^{n}X_i2^{-i}\
X=-X_0+\sum{i=1}^{n}X_i*2^{-i}
$$
补码的右移
在补码运算的机器中,一个数不论其正负,连同符号位向右移一位,符号位保持不变,就等于乘1/2.
$$
X=-X_0+\sum_{i=1}^{n}X_i2^{-i}\
1/2X=-1/2X_0+1/2\sum_{i=1}^{n}X_i2^{-i}\
=-X_0+1/2\sum_{i=0}^{n}X_i*2^{-(i+1)}\
补码形式:[1/2X]_补=X_0.X_0X_1X_2……X_n
$$
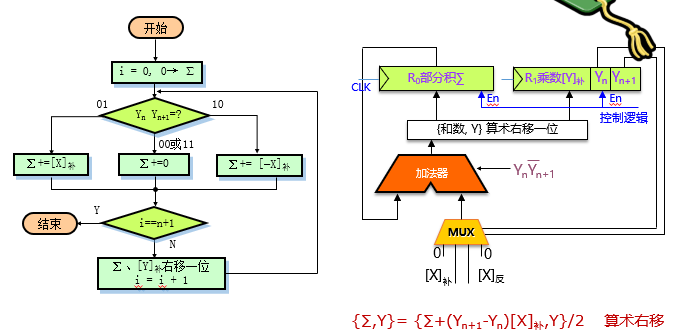
补码乘法规则
$[XY]_补 ≠ [X]_补[Y]_补$
$[XY]_补 = [X]_补Y$
原码乘法的主要问题是符号位不能参加运算,单独用一个异或门产生乘积的符号位。故自然提出能否让符号数字化后也参加乘法运算,补码乘法就可以实现符号位直接参加运算。

乘法运算器设计
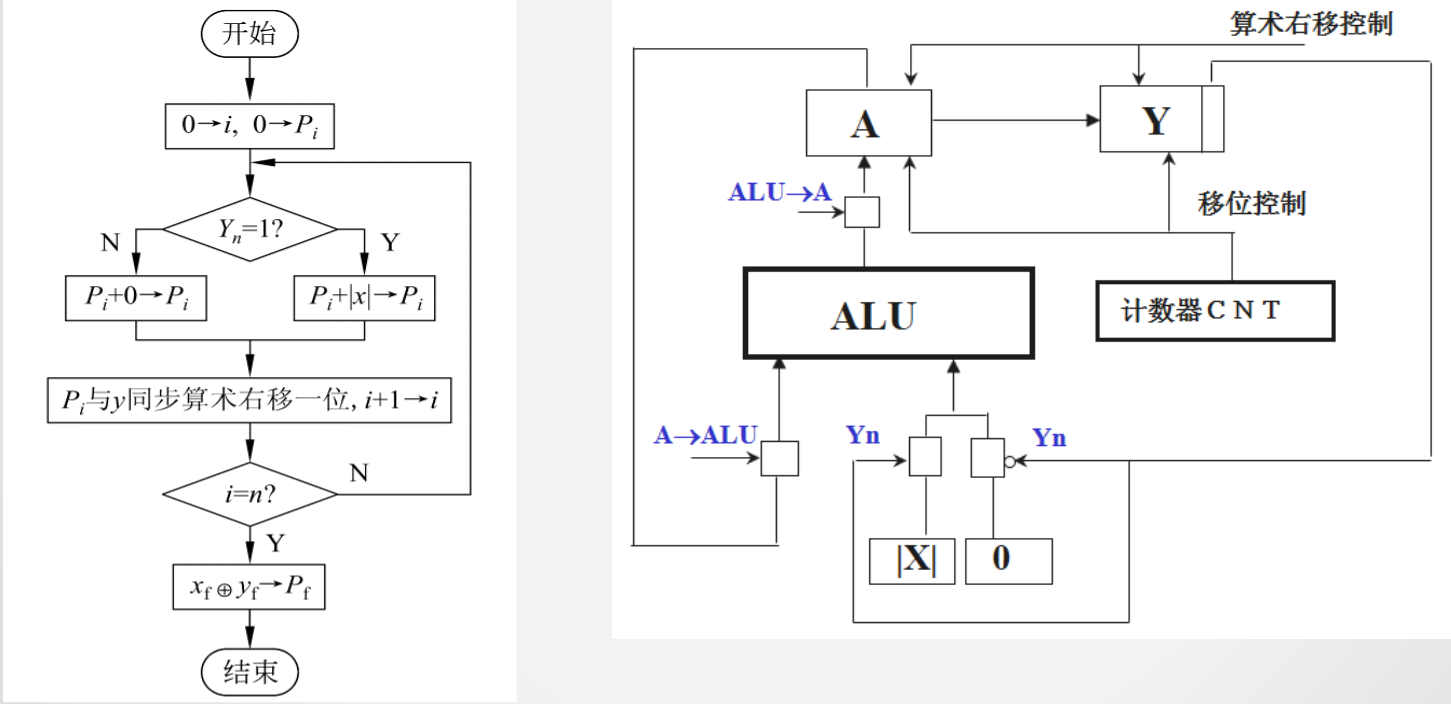
原码一位乘法器设计
- 作完加法,一定移位
- n次加法
- 符号位单独计算
核心运算
累加 ∑ = ∑ + 0 ∑ = ∑ + X
逻辑右移 ∑ = ∑ / 2
分支合并
累加 ∑ = ∑+YnX 节约多路选择器
减少寄存器访问
∑ = (∑ +YnX)/2
先移位再锁存,提升速度
运算计数控制
简单状态机控制,计数器比较
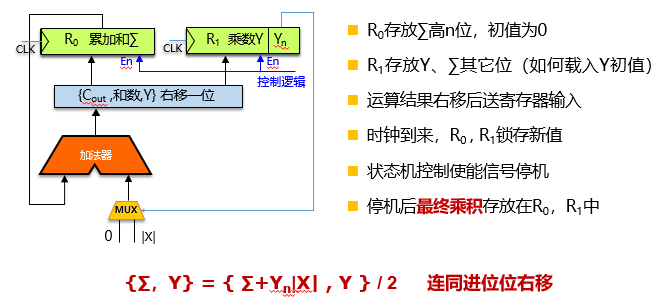

补码一位乘法设计
- n+1次加法
- 符号位参与运算
- 不需要单独计算符号位
例子:

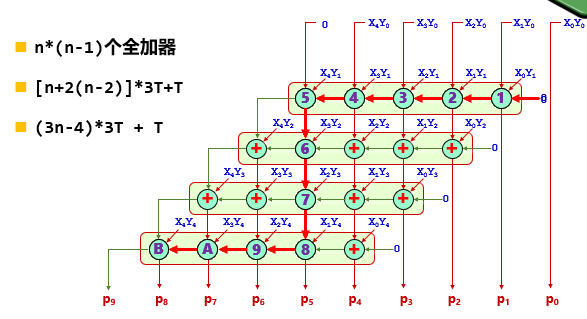
阵列乘法器设计
阵列乘法器的设计目的是为了避免原码一位乘法器中不断循环累加造成的时间浪费
阵列包括了:与门阵列和FA阵列
横向进位阵列乘法器时延分析:
每一行加法器都存在串行进位的关系
6必须等到5计算后才能接着计算(6接收的是5的运算值,把它当作x、y)
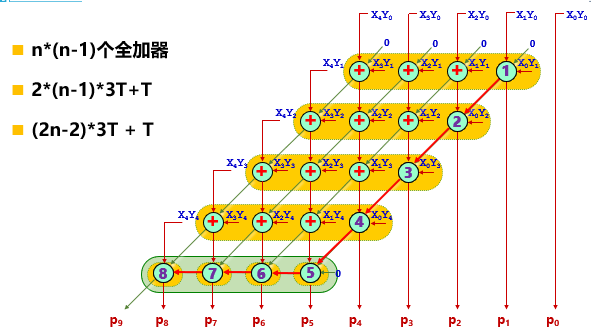
斜向进位阵列乘法器时延分析
将进位送入下一级后,同级的FA之间就不存在串行关系。原因在于:1的进位值对P2产生影响,故1的进位值送入左边还是下一级的2都不会对结果产生影响。
最后一行是串行FA。因为没有下一级送进位了,故只能串行送。
定点数除法
恢复余数除法(绝对值)
当余数为正数:够减,商上1,余数左移一位,再与除数做减法比较
当余数为负数:不够减,商上0
1、加除数恢复成原来的值,将余数左移一位,再与除数做减法比较
重复直至商满足要求。


因为要恢复余数,所以运算步数是不确定的。
上商是根据余数是否>0
加/减交替除法(不恢复余数法)
当余数小于0的时候,不需要恢复余数,余数左移+y。

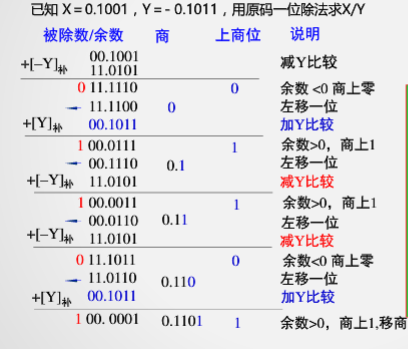
上商是根据左移出的哪位来上的。
浮点数加减运算
浮点数规格化:把一个浮点数转化成指定的格式。
尾数规格化:00.1xxxxx或者11.0xxxxx
步骤
1、对阶
将两个数的阶码转化成一样大小。这样有一个数的尾数将会发生改变
2、尾数的运算
将对阶后的尾数进行加减运算
3、尾数规格化处理
对加减运算后的尾数进行规格化处理,同时阶码也改变了
4、舍入
0舍1入。如果没有丢掉有效数字,就不需要舍入。
5、浮点数的溢出处理
因为是双符号数,溢出规则同双符号数的溢出规则。
上溢:超出所能表示的最大正数
下溢:超出所能表示的最小负数