单源最短路径

最短路径问题：一个带权重的有向图G = (V, E)和权重函数w: E->R，该权重函数将每条边映射到实数值的权重上。一条路径p的权重w(p)是构成该路径的所有边的权重之和，定义从节点u到结点v的最短路径权重δ (u, v)如下：

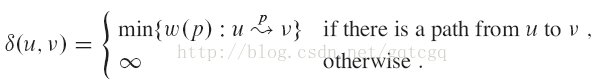
单目的地最短路径问题：找出从每个顶点v到指定终点t的最短路径。把图中的每条边反向，就可以把这一问题变为单源最短路径问题。

一些概念：

如果一条路径中包含两个相同的结点，则该路径包含环路。

不包含环路的路径称为简单路径。

最短路应为简单路径，不包含环路。

对任何简单路径最多包含|V|-1条边和|V|个结点。
不失一般性，假设后续算法寻找的最短路径都不包含环路。

负权重边

边的权重可以为负值，即使边的权重为负值，对于所有节点v，最短路径权重 (u, v)都可以有精确定义。但是，如果图G=(V, E)包含从源节点s可以到达的，权重为负值的环路，则最短路径权重无定义，从s到该环路上的任意节点的路径都不可能是最短路径。如果从节点s到节点v的某条路径上存在权重为负值的环路，则(u, v) = -∞。

示例：

从节点s到节点c有无数条路径；<s,c>, <s,c,d,c>,<s,c,d,c,d,c>等，因为环路<c, d, c>的权重为3>0。所以从s到c的最短路径为<s,c>，δ(s, c)=5。

从节点s到节点e也有无数条路径：<s,e>, <s,e,f,e>, <s,e, f,e, f,e >等，因为环路<e, f, e>的权重为-3，所以，从节点s到节点e没有最短路径，因此δ(s,e)=-∞。类似的， δ(s,f)=-∞。因为g可以从节点f到达，所以， δ(s, g)=-∞。（因为s到e可以在e、f上转圈圈，就会使得路径趋于负的无穷小）

最短路径的表示

一个结点的前驱结点记为：v.π
（前驱结点或者为NIL或者为另一个结点）

利用v.π的记录可以搜索出最短路径上的所有结点。

一个源点s所诱导的前驱子图定义为Gπ=(Vπ，Eπ)，其中，

结点集合Vπ={v∈V：v.π≠NIL}∪{s}

即Vπ是源点s和图G中的前驱结点不为NIL的所有结点的集合

边集合Eπ={(v.π,v)∈E：v∈Vπ-{s}}

即Eπ是由Vπ中的结点v的π值所“诱导”(induced)的边的集合。

则，算法终止时，Gπ是一棵最短路径树。

该树包含了从源点s到每个可以从s到达的结点的最短路径。

另外，最短路径不是唯一的，最短路径树也不一定是唯一的。

松弛操作

松弛：原来用一根橡皮筋连接p和w两点，现在有一点v到w的路径更短，现在把橡皮筋w点的另一端p换成v点，这样缓解橡皮筋紧绷的压力，让其变得松弛。

简单的说就是不断更新最短路径。

1）松弛边： w -> v 意味着先检查从s到v的最短路径是否是先从s 到 w，再由w -> v, 如果是，则更新v.d和v.π的数据。

//对于每个顶点v∈V，都设置一个属性d[v]，用来描述从源点s到v的最短路径上权值的上界，称为**最短路径估计（shortest-path estimate）**。π[v]代表S到v的当前最短路径中v点之前的一个点的编号
private void relax(DirectedEdge e)
    {
        int v = e.from(), w = e.to();
        if (v.d  >  w.d + e.Weight())
        {
            v.d = w.d + e.Weight();
            v.π = e;
        }
    }
//RELAX 的时间：O(1)

最短路径和松弛操作的性质

1。三角不等式性质：对于任何边(u,v)∈E，有δ(s,v)≤δ(s,u)+ω(u,v)。

证明：

假定p是从源结点s到结点v的一条最短路径，则p的权重不会比任何从s到v的其它路径的权重大，因此路径p的权重也不会比这样的一条路径的权重更大：从源结点s到结点u的一条最短路径，再加上边(u,v)而到达结点v的这条路径。

如果s到v没有最短路径，则不可能存在s到v的路径。

2。上界性质：对于所有结点v∈V，我们有v.d≥δ(s,v)。一旦v.d的取值达到δ(s,v)，其值将不再变化。

证明：

使用数学归纳法

3。非路径性质：若从结点s到结点v之间不存在路径，有v.d=δ(s,v)=∞。

证明：

因为从源点s到给定点v之间不存在路径，所以δ(s,v)=∞。而根据上界性质，总有v.d≥δ(s,v)，所以，v.d≥δ(s,v)=∞。

4。收敛性质：设结点u,v∈V，如果s⇝u→v是图G中的一条最短路径，且在对边(u,v)进行松弛前的任意时间有u.d=δ(s,u)，则在之后的所有时间有v.d=δ(s,v)。

5。路径松弛性质：若p=<v0,v1,…,vk>是从源结点s=v0到结点vk的一条路径，且我们对p中所进行松弛的次序为(v0,v1),(v1,v2),…,(v~~k−1~~,vk)，则vk.d=δ(s,vk)。

该性质的成立与其他边的松弛操作及次序无关，即使这些松弛操作是与对p上的边所进行的松弛操作穿插进行的。

数学归纳法证明。

6。前驱子图性质：对于所有结点v∈V，一旦v.d=δ(s,v)，则前驱子图是一棵根结点为s的最短路径树。

最短路径的最优子结构

最短路径具有最优子结构性质：两个结点之间的一条最短路径包含其他的最短路径

具有==贪心思想==

证明（剪枝-复制法+反证法）

假设路径p分为poi 、pij、pjk ，并且p是vo到vk的最短路径。如果poi 、pij、pjk不是最短路径的话，假设存在p~~oi2~~

是vo到vi 的最短路径。将poi 减去复制上p~~oi2~~ 就反证出p不是最短路径，矛盾。

Bellman-ford算法

适用条件&范围

单源最短路径(从源点s到其它所有顶点v);——可以有负权重的边，但不能有负权重的环
有向图&无向图(无向图可以看作(u,v),(v,u)同属于边集E的有向图);
边权可正可负(如有负权回路输出错误提示);
差分约束系统;

步骤

第一，初始化所有点。每一个点保存一个值，表示从原点到达这个点的距离，将原点的值设为0，其它的点的值设为无穷大（表示不可达）。

第二，进行循环，循环下标为从1到n－1（n等于图中点的个数）。在循环内部，遍历所有的边，进行松弛计算。（对于N个点，进行N次循环，每次循环依次更新路径）

第三，遍历途中所有的边（edge（u，v）），判断是否存在这样情况：
d（v） > d (u) + w(u,v)（三角不等式性质）
则返回false，表示途中存在从源点可达的权为负的回路。

松弛迭代（核心）

参考文章

大致意思就是，每次对所有边进行松弛，就算一次松弛迭代：

性质一：一般性的，当图中已经存在一个或多个已确认顶点时，即图处于任意一种状态，若图中尚存在未确认顶点，则执行一次迭代后，会增加至少一个已确认顶点。

证明：

性质二：若图中存在由起点不可达的顶点，则这些顶点的初始化状态即为最短路径状态，即初始化时就处于已确认状态。

证明：

所以Bellman-ford算法的循环次数：

松弛边按照最坏情况下进行，即一次只增加一个已确认顶点，则需要执行的迭代次数为 |V|-1次
松弛边按照最好情况下进行，则需要执行的迭代次数为 1 次。

检测带权有向图中是否存在负权回路

根据前面对松弛函数执行次数的分析可知，若图中不存在负权回路，那么即使在最坏情况下，也只需要执行 |V|-1 次迭代松弛，即可获得从起点到各顶点的最短路径。

若图中存在负权回路，当回路较小时，例如顶点自身或者两个顶点之间的负权回路，则在 |V|-1 次迭代过程中，可能多次通过了该负权回路；若回路较大，例如从起点出发，串联所有顶点最后回到起点，即通过 |V|-1 条边构成一个圆形，如下图所示。则 |V|-1 次迭代过程中，可能一次也不会通过该负权回路，但是当再执行一次迭代松弛，即可将 ds 值更新为负值，所以可以多执行一次迭代，通过判断是否更新从起点到某个顶点的最短路径权值，来判断图中是否存在负权回路。

算法描述

BELLMAN-FORD(G,w, s)

          INITIALIZE-SINGLE-SOURCE(G, s)
          for i = 1 to |G.V|-1
                 for  each edge (u, v)∈ E
                        RELAX(u, v, w)
                for each edge (u, v) ∈ E
                 if  v.d > u.d + w(u, v)
                        return  FALSE
                        
                             return TRUE

算法证明

根据最优子结构性和松弛迭代就可以证明：

如果图G中不包含从源结点s可以到达的权重为负值的环路，则算法将返回TRUE，且对于所有结点v∈V，前驱子图Gπ是一个根结点为s的最短路径树。

如果结点v是从s可以到达的，则论断可以从松弛迭代和最优子结构性得到证明。

如果结点v不能从s可达，则论断可以从非路径性质获得。

综合前驱子图性质和本论断，可以推导出Gπ是一棵最短路径树
如果图G中包含一条从源结点s可以到达的权重为负值的环路，则算法将返回FALSE。

三角不等式性质。可以使用反证法说明

时间性能

初始化：Θ(V)

松弛处理：for循环执行|V|-1次，每次的时间是Θ(E)

Bellman-ford算法总的运行时间是O(VE)。

Dijkstra算法（贪心算法）

Dijkstra算法解决带权重的有向图上单源最短路径问题

**==该算法要求所有边的权重为非负值==**，如果采用合适的实现方式，Dijkstra算法的运行时间要比Bellman-Ford算法快。

算法思路

保存两个集合S和U，S用于存放已经找到和起点之间最短距离的点，U用于存放尚未找到最短距离的点，起初S中只有起点，其余所有的点存放在U中，并根据和起点是否相邻，修改了距离起点的距离，不相邻则默认为无穷远。
循环遍历U中的点，找出离起点距离最近的点，该点到起点的距离就是该点到起点的最短距离，将该点从U中移除并放置到S中去，并重新计算U中的点距离起点的距离。这样每次选取的点都是剩余点中距离起点最近的点。
循环上述操作，直到找到终点到起点的最短路径或则循环结束。

Dijkstra算法是一个贪心算法：每次总是选择V-S集合中最短路径估计值最小的结点加入S中。

算法描述

DIJKSTRA(G, w, s)
              INITIALIZE-SINGLE-SOURCE(G, s)//对所有节点的d值和派值初始化
              S = ∅
              Q =G.V
              while Q != ∅
                     u = EXTRACT-MIN(Q)
                     S= S ∪  {u}
                     for  each vertex v ∈ G.Adj[u]//对所有从u出发的边进行松弛
                            RELAX(u, v, w)

算法证明

利用循环不变式证明循环不变式：

算法在while语句的每次循环开始前，对于每个结点u∈S，有u.d=δ(s,u)

只需证明：对于每个结点u∈V，当u被加入到S时，有u.d=δ(s,u)。注：一旦u加入S，就不会再修正u.d。且根据上界性质，该等式将一直保持。

证明过程：

（1）初始化：初始时，S=Ø，因此循环不变式直接成立。

（2）保持：在每次循环中，对于加入到集合S中的结点u而言，u.d=δ(s,u)。

用反证法证明：设结点u是第一个在加入到集合S时u.d≠δ(s,u)的结点。

由于s是第一个加入到集合S中的结点，并且s.d=δ(s,s)=0，所以u≠s，并且在u即将加入S时，S≠Ø，因为S中至少包含了s。故，此时必存在至少一条从s到u的路径（否则，根据非路径性质将有u.d=δ(s,u)=∞，与假设的u.d≠δ(s,u)相矛盾，故这样路径一定存在），这样也必存在一条从s到u的最短路径，记为p。

取p路径上的一个点x（该点是s到u的中间点）在结点u加入到集合S时，有x.d=δ(x,y)【因为u是第一个不满足关系的点，并且每次S取的点都是剩下点中具有最短路径的点，x.d<=u.d。它肯定被取入S中了】

然后取p路径上的y点，该点的前驱节点为x。则有：在结点u加入到集合S时，应有y.d=δ(s,y)。这是因为x∈S，u是第一个u.d≠δ(s,u)的结点，在将x加入到集合S时，有x.d=δ(s,x)，y是x的邻接点，所以此时边(x,y)将被松弛。由于y是最短路径p上的结点，根据最短路径的最优子结构性和收敛性质，此时应有y.d=δ(s,y)。

因为结点y是从结点s到结点u的一条最短路径上位于u前面的一个结点，所以应有δ(s,y)≤δ(s,u)，即y.d<=u.d。

但是我们注意到，此时取进S集合的是u不是y，所以u.d应该小于等于y.d。矛盾

时间性能

根据算法的处理规则，每个结点u仅被加入集合S一次，邻接链表Adj[u]中的每条边在整个运行期间也只被检查一次。因此算法第7-8行的for循环执行次数总共为|E|次（即松弛判定总次数）

Dijkstra算法的总运行时间依赖于最小优先队列Q的实现。

如果用线性数组(无序或者按序插入)实现，每次找d最小的结点u需要O(V)的时间，所以算法的总运行时间为O(V^2^+E)=O(V^2^)。
如果用二叉堆实现，每次找d最小的结点u需要O(lgV)的时间，所以算法的总运行时间为O((V+E)lgV)。
如果用斐波那契堆实现，算法的总运行时间可以改善至O(VlgV+E)。

差分约束和最短路径

对于一组不等式：
$$
\begin{cases}
x_1-x_2≤0\
x_1-x_5≤1\
x_2-x_5≤1\
x_3-x_1≤5\
x_4-x_1≤4\
x_4-x_3≤-1\
x_5-x_3≤-3\
x_5-x_4≤-3\
\end{cases}
$$
特点是全都是两个未知数的差小于等于某个常数（大于等于也可以，因为左右乘 −1-1−1 就可以化成小于等于的形式），这样的不等式组称作差分约束系统。

这个不等式组要么无解，要么就有无限组解。因为如果存在一组解(x1,·····xn)的话，那么对于任何一个常数 k 有

(x1+k,·····xn+k)也肯定是一组解，因为任何两个数加上一个数以后，它们之间的关系（差）是不变的，这个差分约束系统中的所有不等式都不会被破坏。

约束图

每个未知数 xi对应图中的一个顶点vi ，把所有的不等式都化成图中的一条边，对于不等式
$$
x_i−x_j≤ y
$$
化成三角形不等式
$$
x_i≤ x_j+y
$$
就可以化成边 <vj,vi>权值为 y 。最后在这张图上求一遍单源最短路，这些三角不等式就全部满足了，因为它是最短路问题的基本性质。

说明：

（1）结点集合：约束图中引入一个额外的结点v0，从其出发可以达到其他所有结点。因此结点集合V由代表每个变量xi的结点vi和**额外的结点v0**组成。

（2）边集合：边集合E包含代表每个差分约束的边，同时包含v0到其他所有结点的边(v0,vi)，i=1,2，…，n。

（3）边的权重：如果xj-xi≤bk是一个差分约束条件，则边(vi,vj)的权重记为ω(vi,vj)=bk，而从v0出发到其他结点的边的权重ω(v0,vj)=0

图中每一条边都代表差分约束系统的一个不等式。现在以 v0为源点，求单源最短路，最终得到的v0到 vi的最短路径长度就是 xi的一个解。如图中 v0到其他各个顶点的最短距离分别是 {−5,−3,0,−1,−4}{-5,-3,0,-1,-4}{−5,−3,0,−1,−4} ，因此满足上述不等式的一组解就是 {x1,x2,x3,x4,x5}={−5,−3,0,−1,−4} 。当然把每个数都加上 101010 也是一组解 {5,7,10,9,6}{5,7,10,9,6}{5,7,10,9,6} ，但是这组解只满足不等式组 (1) ，也就是原先的差分约束系统，而不满足不等式组 (2) ，也是我们后来加上的那些不等式。当然这是无关紧要的，因为 x0本来就是个局外人，并不在乎它。

对于上面例子而言，它代表的解 x0值也在其中也就是 x0=0。但是 x0的值是无可争议的，既然是以它作为源点求最短路径，那么源点到它的最短路径当然是 0了，因此，我们解这个差分约束系统无形中存在一个条件x0=0那么它有什么用呢？可以限制所有的未知数的解都不大于0 。

解的个数：

(1) 如果图G不包含权重为负值的回路，则是该系统的一个可行解。

(2) 如果图G包含权重为负值的回路，则该系统没有可行解

一个有趣的结论：当我们一开始就把 v0的解死定为 A 的时候，所有未知数的解都不会大于 A （一开始把 dis[0]=A）