递归

本文希望总结一下递归的用法和理解。

什么是递归

递归是什么呢？简单的说就是函数自身调用自身，可以间接调用也可以直接调用。在实际问题的解决中，调用递归可以把一个大型的问题层层转化成一个规模缩小的同类问题的子问题，然后递归调用方法来表示问题的解。

在实际实现递归过程中，一定要理解“我们只需要关注一级递归的解决过程即可。”这句话的含义。可以把之前的多层递归体看成是一个总体，再考虑问题。

递归和迭代的区别

迭代和递归的区别是：迭代使用的是循环结构，递归使用的是选择结构。

• 递归能使程序的结构更清晰、更简洁、更容易让人理解，从而减少读懂代码的时间。但是大量的递归调用会建立函数的副本，会耗费大量的时间和内存。
• 迭代则不需要反复调用函数和占用额外的内存。因此我们应该视不同 情况选择不同的代码实现方式。

递归的基本原理

第一：每一级的函数调用都有自己的变量。

第二：每一次函数调用都会有一次返回。 当程序流执行到某一级递归的结尾处时，它会转移到前一级递归继续执行。

第三：递归函数中，位于递归调用前的语句和各级被调用函数具有相同的执行顺序。

第四：递归函数中，位于递归调用后的语句的执行顺序和各个被调用函数的顺序相反。

第五：虽然每一级递归都有自己的变量，但是函数代码并不会得到复制。

第六：递归函数中必须包含可以终止递归调用的语句。称为递归出口。

参见一个经典的例程说明上述：

#include<stdio.h>
void up_and_down(int);
int main(void)
{
   up_and_down(1);
   return 0;
}
void up_and_down(int n)
{
    printf("Level %d:n location %p\n",n,&n); /* 1 */
    if(n<4)
      up_and_down(n+1);
    printf("Level %d:n location %p\n",n,&n); /* 2 */
}

输出结果

Level 1:n location 0240FF48
Level 2:n location 0240FF28
Level 3:n location 0240FF08
Level 4:n location 0240FEE8
Level 4:n location 0240FEE8
Level 3:n location 0240FF08
Level 2:n location 0240FF28
Level 1:n location 0240FF48 

解析：

（1）首先， main() 使用参数 1 调用了函数up_and_down() ，于是 up_and_down() 中形式参数 n 的值是 1, 故打印语句 #1 输出了 Level1 。

（2）然后，由于 n 的数值小于 4 ，所以 up_and_down() （第 1 级）使用参数 n+1 即数值 2 调用了 up_and_down()( 第 2 级 ). 使得 n 在第 2级调用中被赋值 2, 打印语句 #1 输出的是 Level2 。与之类似，下面的两次调用分别打印出 Level3 和 Level4 。

（3）当开始执行第 4 级调用时， n 的值是 4 ，因此 if 语句的条件不满足。这时候不再继续调用 up_and_down() 函数。第 4 级调用接着执行打印语句 #2 ，即输出 Level4 ，因为 n 的值是 4 。现在函数需要执行 return 语句，此时第 4 级调用结束，把控制权返回给该函数的调用函数，也就是第 3 级调用函数。第 3 级调用函数中前一个执行过的语句是在 if 语句中进行第 4 级调用。因此，它继续执行其后继代码，即执行打印语句 #2，这将会输出 Level3。当第 3 级调用结束后，第 2 级调用函数开始继续执行，即输出Level2 ．依次类推．

注意，每一级的递归都使用它自己的私有的变量 n ．可以查看地址的值来证明．此例程也说明了第一点和第二点

**第三点说明： 打印语句 #1 位于递归调用语句前，它按照递归调用的顺序被执行了 4 次． **

第四点说明：#2语句的调用的顺序是相反的

递归的三大要素

第一要素： 明确你这个函数想要干什么。 先不管函数里面的代码什么，而是要先明白，你这个函数的功能是什么，要完成什么样的一件事。

第二要素： 寻找递归结束条件。我们需要找出当参数为啥时，递归结束，之后直接把结果返回，请注意，这个时候我们必须能根据这个参数的值，能够直接知道函数的结果是什么。

在设计递归算法时，要明确该问题的子问题也一定可以用该递归求。

第三要素： 找出函数的返回值。

在分析递归的时候，要从宏观的角度分析，例如树，就只看成根节点、左右节点就行了

递归的过程

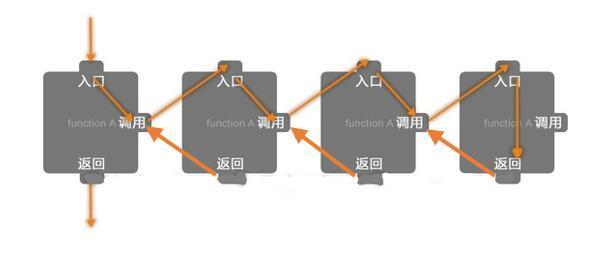
递归和栈的关系

总所周知，递归是一个十分消耗资源的方式。当递归的次数很大的时候会导致函数栈溢出而死机。

调用栈:描述函数之间的调用关系,当函数之间相互调用的时候会使用调用栈;
调用栈由多个栈帧组成,每个栈帧记录着一个未运行完的函数; 栈帧中保存着该函数的返回地址以及局部变量;
在递归中,递归函数的每一次的”递进去”,栈帧都会将上个函数的返回地址局部变量保存以便在返回的过程中找得到相应的”回归出来的方向”
栈帧

1：栈帧将栈分割成N个记录块，每一个记录块的大小是不一样的；
2：这个记录块实际上是编译器用来实现函数调用的数据结构，通俗来讲就是用于活动记录，他用于记录每次函数调用所涉及的相关信息的记录单元；
3：栈帧也是一个函数的执行环境，它包括函数的参数，函数的局部变量函数，执行完之后要返回到哪里等等；

栈帧是用于调用函数的，你每调用一次函数他就会形成一个栈帧用于这个被调用函数的运行环境；

e.g.

function test(n){
        if(n == 1){
            return 1;
        }else if(n <= 0){
            return 0;
        }else{
            return n * test(n-1);
        }
    }
    console.log(test(5));

test(5)先调用，然后栈帧填入递归调用函数的信息。

分析：
要求计算5的阶乘；
1）：调用test函数时传入5，即首先在栈中划出一个记录块做为函数test（5）的执行环境；执行到最后结果为： 5 * test（4）；
2）：上一个函数的返回值中调用函数test（4），因此继续指向新的记录块，用于执行函数test（4）；执行到最后结果为： 4 * test（3）；
3）：上一个函数的返回值中调用函数test（3），因此继续指向新的记录块，用于执行函数test（3）；执行到最后结果为： 3 * test（2）；
4）：上一个函数的返回值中调用函数test（2），因此继续指向新的记录块，用于执行函数test（2）；执行到最后结果为： 2 * test（1）；
5）：上一个函数的返回值中调用函数test（1），因此继续指向新的记录块，用于执行函数test（1）；执行到最后test（1）=1；
此时进栈操作已经到达了递归终止的条件，为了计算出最后的test（5）的值需要执行出栈操作；

如上图，我画了一幅出栈示意图；栈是先进后出的，所以最后进的要先出。
1）：test（1）出栈，返回值为1；
2）：栈帧test（2）接收test（1）返回值进行计算得出test（2） = 2 * 1 = 2；
3）：test（2）出栈，栈帧test（3）接收test（2）返回值进行计算得出test（3） = 3 * 2 = 6；
4）：test（3）出栈，栈帧test（4）接收test（3）返回值进行计算得出test（4） = 4 * 6 = 24；
5）：test（4）出栈，栈帧test（5）接收test（4）返回值进行计算得出test（5） = 5 * 24 = 120；
6）：test（5）出栈，返回值120，此时表示这一段程序已经执行完毕，计算得出5的阶乘是120；
总结：在每一次递归函数调用的时候，栈帧都要记录下一个栈帧的返回值，所以调用的层数就和栈帧数相同

递归的优化方式

考虑是否重复计算

在有重复计算的时候，可以考虑采用map容器将计算过的节点保存起来 每次递归先查找该容器中是否存在该节点(key)，如果存在则直接返回对应的值(value)；否则计算，并将新的节点(key)和值(value)存入map中 。

考虑尾递归

传统的递归是首先执行递归调用，然后获取递归调用的返回值并计算结果。在每次递归调用返回之前是不会得到计算结果的。

在尾递归中，首先执行计算，然后执行递归调用，将当前步骤的结果传递给下一个递归步骤。

function test(n，total=0){
        if(n == 1){
            return 1;
        }else if(n <= 0){
            return 0;
        }else{
            return test(n-1,toal+n);
        }
    }
    console.log(total);

分析：执行的顺序

test(5, 0)
test(4, 5)
test(3, 9)
test(2, 12)
test(1, 14)
test(0, 15)
15

每次递归调用的时候，total的值会更新。

尾递归的原理

当编译器检测到一个函数调用是尾递归的时候，它就覆盖当前的活动记录而不是在栈中去创建一个新的。编译器可以做到这点，因为递归调用是当前活跃期内最后一条待执行的语句，于是当这个调用返回时栈帧中并没有其他事情可做，因此也就没有保存栈帧的必要了。通过覆盖当前的栈帧而不是在其之上重新添加一个，这样所使用的栈空间就大大缩减了，这使得实际的运行效率会变得更高。

一些例程的学习

在上网总结和学习了别人有关递归的博客后，现在分享几道例题来熟悉递归的使用。

Leetcode 104. 二叉树的最大深度

class Solution {
    public int maxDepth(TreeNode root) {
        //终止条件：当树为空的时候结束递归，并返回此时的深度为0
        if(root==null)
            return 0;
        //明确此次递归需要干什么 ：找到当前树的左子树或者右子树中最大深度
        int right = maxDepth(root.right);
        int left = maxDepth(root.left);
        //明确返回值是什么：当前树的最大深度
        return (right>left)?right+1:left+1;
    }
}

Leetcode 24. 两两交换链表中的节点

class Solution {
    public ListNode swapPairs(ListNode head) {
        if(head==null||head.next==null)
            return head;
            //把head next 排号的部分切换成next head 排号的部分
            ListNode next = head.next;
            head.next = swapPairs(next.next);
            next.next = head;
            return next;
    }
}

Leetcode 110. 平衡二叉树

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root==null)
        return true;
        //平衡树的要求：左子树和右子树都是平衡树，并且左子树和右子树的高度差小于等于1
        if(isBalanced(root.left)&&isBalanced(root.right)&&(Math.abs(depth(root.left)-depth(root.right))<=1))
        return true;
        else 
        return false;
    }
    public int depth(TreeNode root)
    {
        if(root==null)java
        return 0;
        int r = depth(root.right);
        int l = depth(root.left);
        return (r>l)?r+1:l+1;
        }
}

Leetcode 101. 对称二叉树

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return isS(root,root);
    }
    public boolean isS(TreeNode a,TreeNode b)
    {
        if(a==null&&b==null)
        return true;
        if(a==null||b==null)
        return false;
        //对称树的要求
        //递归过程：

//判断两个指针当前节点值是否相等
//判断 A 的右子树与 B 的左子树是否对称
//判断 A 的左子树与 B 的右子树是否对称
        if(a.val==b.val)
        return isS(a.left,b.right)&&isS(a.right,b.left);
        return false;

    }
}

Leetcode 111. 二叉树的最小深度

class Solution {
    public int minDepth(TreeNode root) {
      if(root==null)return 0;
      //求最小深度的时候，要注意是和叶子的距离。也就是说，当你左子树或者右子树没有节点的时候，你只能和另一边的叶子比较最短距离
        //在计算最大深度的时候，这点是包含在算法里面的。
      if(root.left==null)return minDepth(root.right)+java1;
        if(root.right==null)return minDepth(root.left)+1;
       return Math.min(minDepth(root.left),minDepth(root.right))+1;
    }
    
}

Leetcode 226. 翻转二叉树

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root==null)
        return null;
        //翻转二叉树：左右子树交换即可。
        TreeNode temp = root.right;
        root.right = invertTree(root.left);
        root.left = invertTree(temp);
        return root;
    } 
}

Leetcode 617. 合并二叉树

Leetcode 654. 最大二叉树

Leetcode 83. 删除排序链表中的重复元素

Leetcode 206. 翻转链表

Leetcode 38.报数

Leetcode 46.全排序

Leetcode 39.组合总和

Leetcode 40.组合总和2

Leetcode 22.括号生成

Leetcode 98.验证二叉搜索树

//下列做法不能满足节点的左右子树中的所有节点都满足要求
class Solution {
    TreeNode pre = new TreeNode();
    public boolean isValidBST(TreeNode root) {
        if(root==null)return true;
        if(root.left!=null&&root.left.val>=root.val)return false;
        if(root.right!=null&&root.right.val<=root.val)return false;
        boolean left = isValidBST(root.left);
        boolean right = isValidBST(root.right);
        return left&&right;
    }
}
//正确做法
class Solution {
    TreeNode pre = new TreeNode();
    public boolean isValidBST(TreeNode root) {
        if(root==null)return true;
        if(root.right!=null){//保证右子树中的所有节点都满足要求
            pre=root.right;
            while(pre.left!=null){pre=pre.left;}
            if(pre.val<=root.val)return false;
        }
        if(root.left!=null){//保证左子树中的所有节点都满足要求
            pre=root.left;
            while(pre.right!=null){pre=pre.right;}
            if(pre.val>=root.val)return false;
        }
        boolean left = isValidBST(root.left);
        boolean right = isValidBST(root.right);
        return left&&right;
    }
}
//中序遍历递归版本
class Solution {
    long pre = Long.MIN_VALUE; // 记录上一个节点的值，初始值为Long的最小值

    public boolean isValidBST(TreeNode root) {
        return inorder(root);
    }

    // 中序遍历
    private boolean inorder(TreeNode node) {
        if(node == null) return true;
        //访问左子树
        boolean l = inorder(node.left);
        //访问当前节点：如果当前节点小于等于中序遍历的前一个节点，说明不满足BST，返回 false；否则继续遍历。
        if(node.val <= pre) return false;
        pre = node.val;
        boolean r = inorder(node.right);
        return l && r;
    }
}

Leetcode 395.至少有k个重复字符的最长子串

Leetcode 397.整数替换

leetcode 538.把二叉搜索树转换为累加树

//将每个节点的值修改为原来的节点值加上所有大于它的节点值之和
class Solution {        
    int sum=0;
    public TreeNode convertBST(TreeNode root) {
        if(root!=null)
        {
            convertBST(root.right);
            sum+=root.val;
            root.val=sum;
            convertBST(root.left);
        }
        return root;
    }
}

Leetcode 669.修剪二叉搜索树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root==null)return null;
        if (root.val < low) {
            //因为是二叉搜索树,节点.left < 节点 < 节点.right
            //节点数字比low小,就把左节点全部裁掉.
            root = root.right;
            //裁掉之后,继续看右节点的剪裁情况.剪裁后重新赋值给root.
            root = trimBST(root, low, high);
        } else if (root.val > high) {
            //如果数字比high大,就把右节点全部裁掉.
            root = root.left;
            //裁掉之后,继续看左节点的剪裁情况
            root = trimBST(root, low, high);
        } else {
            //如果数字在区间内,就去裁剪左右子节点.
            root.left = trimBST(root.left, low, high);
            root.right = trimBST(root.right, low, high);
        }
        return root;
    }
}

递归改非递归的一般算法

递归的本质是通过栈来保存状态，然后再次调用自己进入新的状态，然后函数返回的时候回到上次保存的状态。

尾递归可以直接转化成循环，这里不多做分析

更一般的递归，想要转化为非递归，就需要模拟栈的行为。

例如：DFS的递归和非递归算法：

/*
假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为初始出发点(源点)，则深度优先遍历可定义如下：首先访问出发点v，并将其标记为已访问过；然后依次从v出发搜索v的每个邻接点w。若w未曾访问过，则以w为新的出发点继续进行深度优先遍历，直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点作为新的源点重复上述过程，直至图中所有顶点均已被访问为止。
　　图的深度优先遍历类似于树的前序遍历。采用的搜索方法的特点是尽可能先对纵深方向进行搜索。这种搜索方法称为深度优先搜索(Depth-First Search)。相应地，用此方法遍历图就很自然地称之为图的深度优先遍历
*/
/*
（1）访问顶点v；

（2）从v的未被访问的邻接点中选取一个顶点w，从w出发进行深度优先遍历；

（3）重复上述两步，直至图中所有和v有路径相通的顶点都被访问到。
*/
void PreorderRecursive(Bitree root){
  if (root) {
    visit(root);
    PreorderRecursive(root->lchild); 
    PreorderRecursive(root->rchild); 
  }
}

/*
1首先初始化待使用栈，然后将第一个结点入栈
2然后只要栈不空，重复下面的操作：将栈顶元素弹出，然后看该元素是否访问过
3若没访问过，则访问，置访问标记，然后将该元素的所有相邻顶点入栈（注意是全部，所以应用一个for或while循环来判断哪些元素该入栈）
4重复2，直至全部顶点均被访问过。
*/
void PreorderNonRecursive(Bitree root){
  stack stk;
  stk.push(root);//节点入栈
  while(!stk.empty()){
    p = stk.top();//栈顶元素出栈并且访问该节点
    visit(p);
    stk.pop();
    if(p.rchild) stk.push(p.rchild);//右边节点入栈
    if(p.lchild) stk.push(p.lchild);
  }
}

这里的非递归中使用栈将结点的相邻结点入栈就是模拟了递归中当一个结点被访问回退时，其相邻结点是和该结点处于同一层次的，故要一起入栈